Excelで超幾何分布を使用する方法
超幾何分布は、この特性を持つK 個のオブジェクトを含むサイズNの有限母集団から、 n回の描画で特定の特性を持つk個のオブジェクトを非置換で選択する確率を表します。
確率変数Xが超幾何分布に従う場合、特定の特性を持つk 個のオブジェクトが選択される確率は、次の式で求められます。
P(X=k) = K C k ( NK C nk ) / N C n
金:
- N:人口規模
- K:母集団内の特定の特性を持つオブジェクトの数
- n:サンプルサイズ
- k:サンプル内の特定の機能を持つオブジェクトの数
- K C k :一度に k 個の K 個のものの組み合わせの数
Excel で超幾何分布に関連付けられた確率を計算するには、次の式を使用できます。
=HYPGEOM.DIST(sample_s, number_sample, population_s, number_pop, cumulative)
金:
- sample_s : サンプルの成功数
- number_samp : サンプルサイズ
- Population_s : 母集団内の成功の数
- number_pop : 人口規模
- cumulative : 累積分布関数を計算するかどうか
次の例は、この公式を実際に使用する方法を示しています。
例 1: デッキからカードを選択する
標準的な 52 枚のカード デッキには 4 人のクイーンがいます。デッキからカードをランダムに選択し、その後、置き換えることなく、デッキから別のカードをランダムに選択するとします。両方のカードがクイーンである確率はどれくらいですか?
Excel で次の式を使用して、カードがクイーンである確率を計算できます。
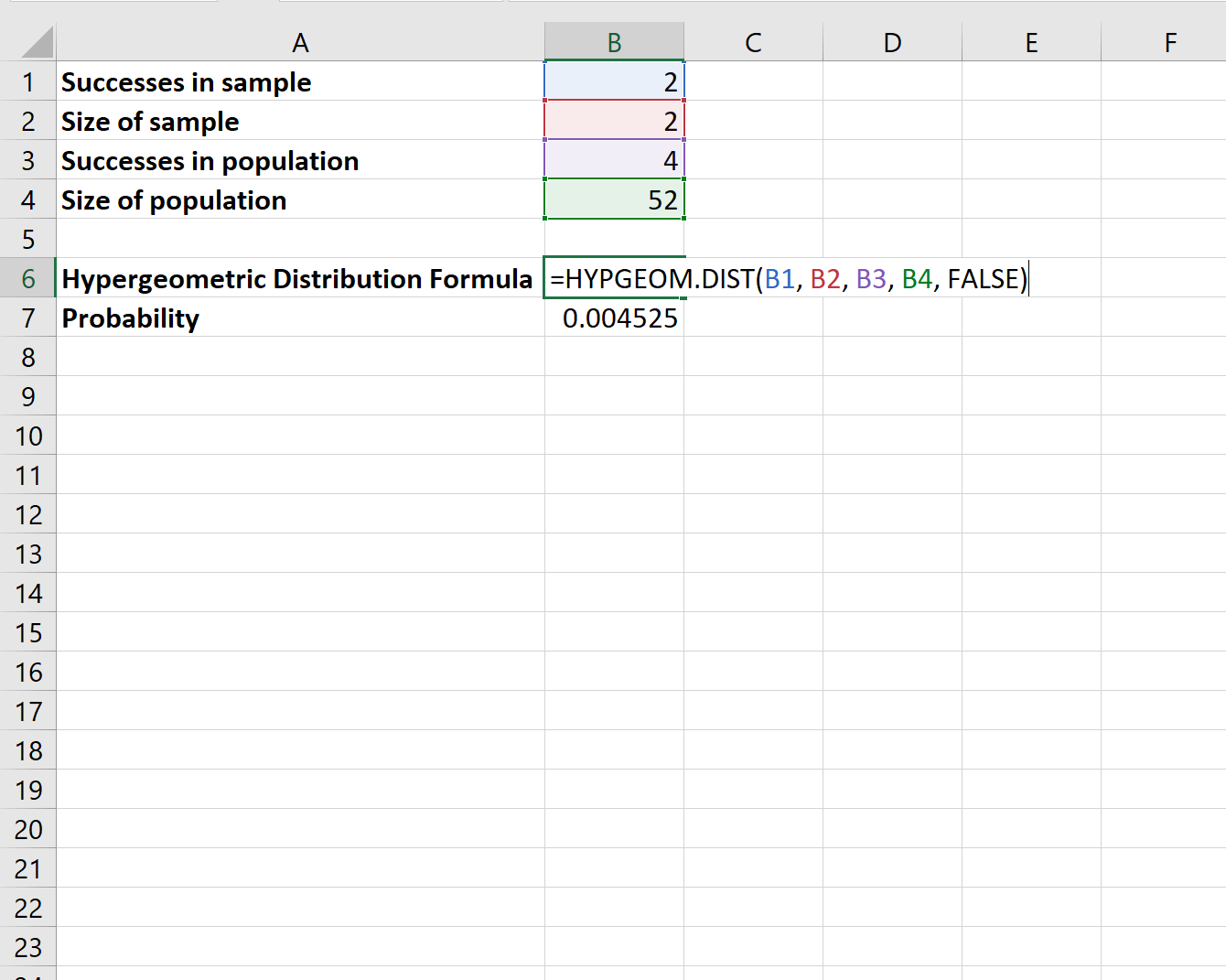
両方のカードがクイーンである確率は です。 00452 。
例 2: 壺からボールを集める
壺には赤いボールが 3 つ、緑色のボールが 5 つ入っています。ランダムに 4 つのボールを選択します。ちょうど 2 つの赤いボールを選択する確率はどれくらいですか?
Excel で次の数式を使用して、この確率を求めることができます。
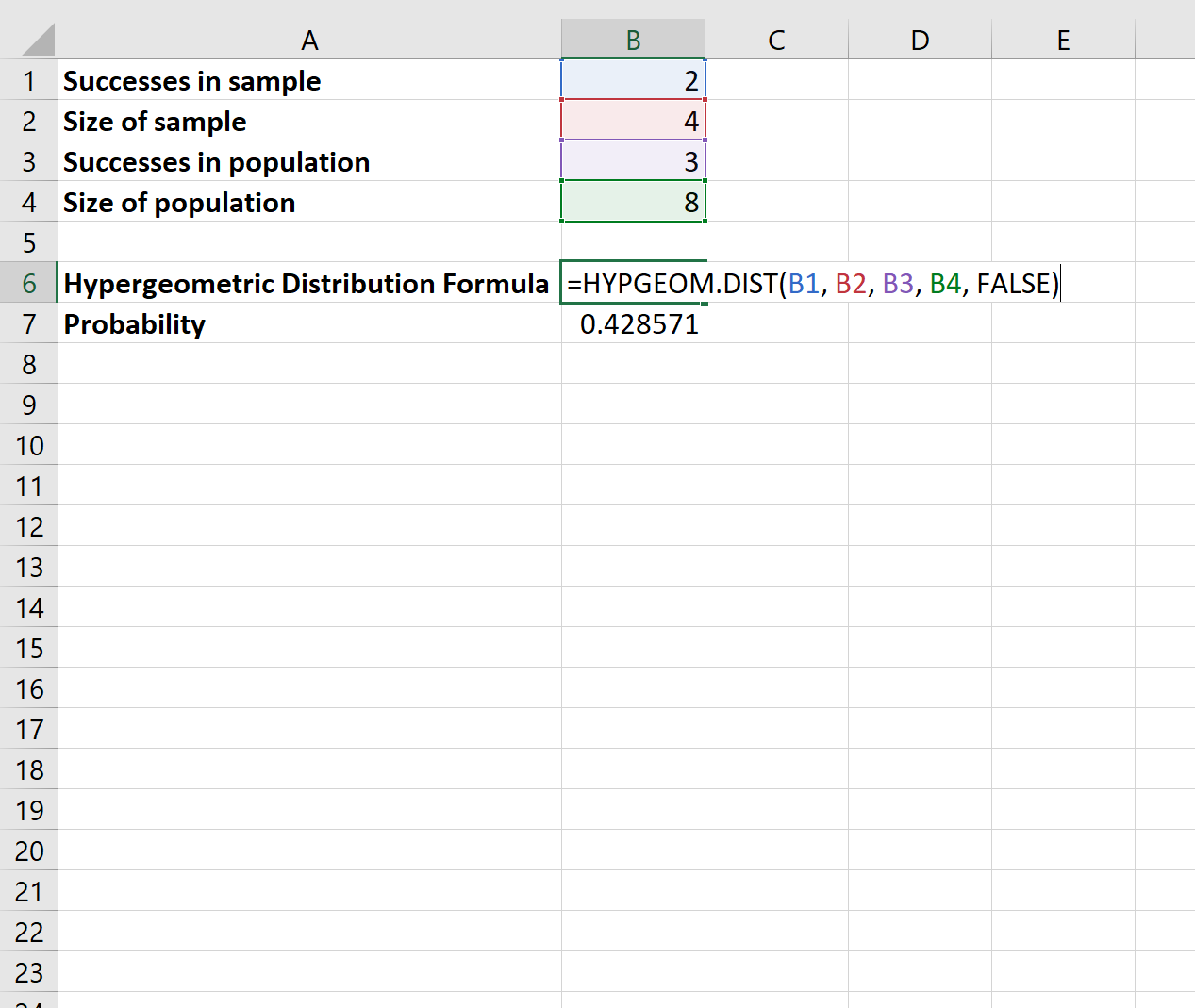
あなたがちょうど 2 つの赤いボールを選ぶ確率は です。 428571 。
例 3: かごからビー玉を選ぶ
かごには紫色のビー玉が 7 個とピンク色のビー玉が 3 個入っています。ランダムに 6 つのビー玉を選択します。ピンクのビー玉をちょうど 3 つ選ぶ確率はどれくらいですか?
Excel で次の数式を使用して、この確率を求めることができます。
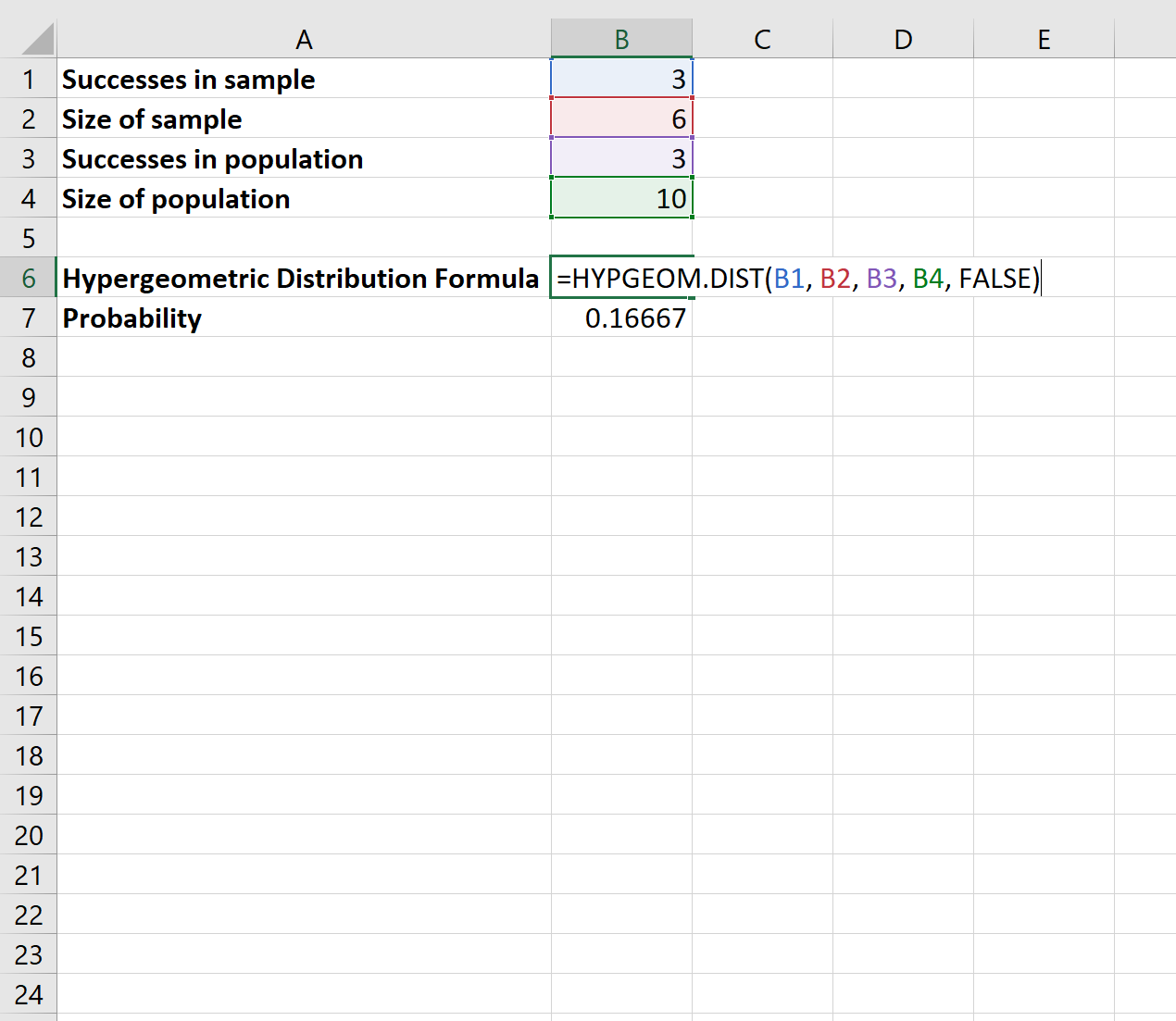
ピンクのビー玉をちょうど 3 つ選ぶ確率は です。 16667 。