共分散行列
この記事では、共分散行列とは何か、またその公式が何であるかを説明します。具体的な例と共分散行列のプロパティを使用して共分散行列を作成する方法を学びます。
共分散行列とは何ですか?
共分散行列は、調査対象の変数の分散と共分散を要素とする正方行列です。したがって、共分散行列の主対角の要素は各変数の分散であり、残りの要素は変数間の共分散です。
統計学では、共分散行列は 2 つ以上の確率変数間の関係を分析するために使用されます。共分散行列は、変数のすべての共分散の値を同時に確認できるため、多くの変数間の相関関係を迅速に解釈できるため、非常に便利です。
共分散行列の記号はギリシャ文字の大文字シグマ (Σ) です。
共分散行列の計算方法
いくつかの統計変数の共分散行列を計算するには、次の手順を実行する必要があります。
- すべての変数の分散を計算します。
- 変数の各ペアの共分散を計算します。
- 共分散行列を作成します。
- 変数iの分散は、行列の主対角線上、より正確には位置i,iに配置する必要があります。
- 変数iとjの間の共分散は、行列の位置i,jに入れる必要があります。
したがって、共分散行列の式は次のようになります。
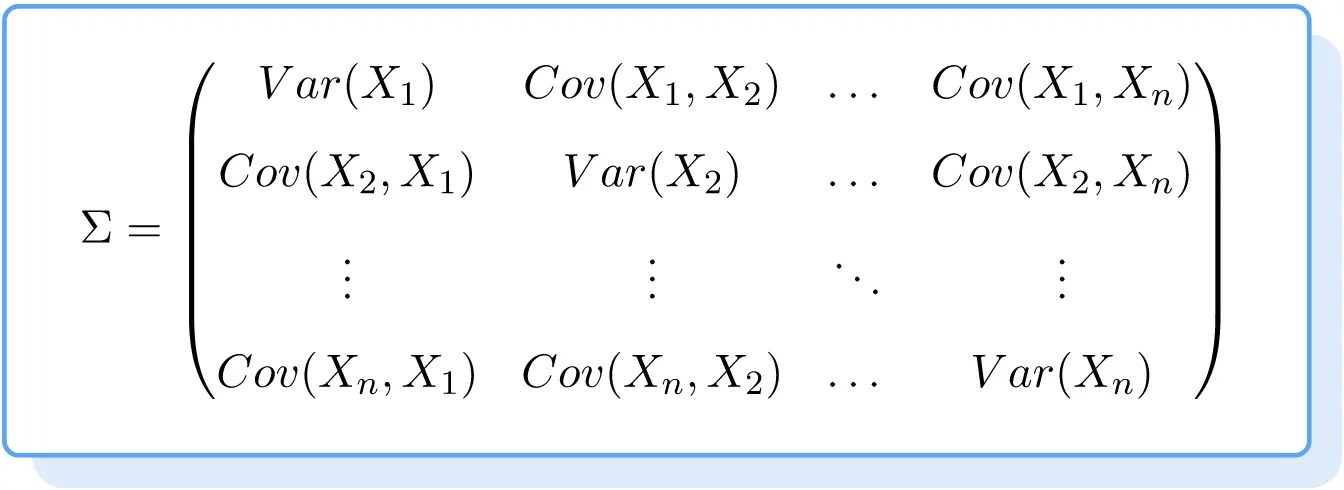
共分散行列の例
共分散行列の定義を確認した後、以下に段階的な演習を示し、このタイプの行列がどのように作成されるかを確認します。
変数 X、Y、Z の共分散行列を計算します。値は次のとおりです。
- ×:4、7、12、5、7
- そして: 9、15、19、6、8
- Z:7、2、4、6、3
最初に行う必要があるのは、すべての変数の分散を決定することです。
![]()
![]()
![]()
次に、変数の各ペア間の共分散を求めます。
![]()
![]()
![]()
すべての分散と共分散を計算したら、あとは共分散行列を作成するだけです。これを行うには、行列の主対角に分散値を配置し、対応する位置に共分散値を配置します。
![Rendered by QuickLaTeX.com \Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3a423b40ad6d25b57327b1f3dccd5df4_l3.png)
![Rendered by QuickLaTeX.com \Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d90c58cc3c8ecef6a85c88196e1dd08d_l3.png)
ご覧のとおり、分散と共分散を行列で表すと、変数を解釈するのが非常に簡単になります。最大の分散を持つ変数は Y (23.44) です。一方、変数 X と Y は直接的な関係にあり、変数 X と Z (したがって Y と Z) は逆の関係にあります。
2 つの変数間の共分散は変数の順序に依存しないため、共分散行列は常に対称であることに注意してください。例えば、
![]()
に等しい
![]()
さらに、共分散行列は常に正方行列となり、その次元は変数の数に等しくなります。この場合、変数が 3 つあるため、行列は 3×3 になりますが、変数が 2 つだけの場合、共分散行列は 2×2 になります。
共分散行列のプロパティ
共分散行列には次の特性があります。
- 共分散行列は変数の数のオーダーの正方行列です。
- 共分散行列は対称です。これは、行列の主対角線が対称軸であることを意味します。
- 共分散行列は常に正の半定値です。
- 共分散行列の行列式はゼロ以上です。