Spss で 1 サンプルの t 検定を実行する方法

1 サンプル t 検定は、母集団の平均が特定の値に等しいかどうかを検定するために使用されます。

このチュートリアルでは、SPSS で 1 サンプルの t 検定を実行する方法を説明します。

例: SPSS での 1 サンプルの t 検定

植物学者は、特定の植物種の平均高さが 15 インチに等しいかどうかを知りたいと考えています。彼女は 12 本の植物からランダムにサンプルを採取し、それぞれの高さをインチ単位で記録します。

次の手順を使用して 1 サンプル t 検定を実行し、次の帰無仮説と対立仮説に基づいて、この植物種の真の平均高さが 15 インチに等しいかどうかを判断します。

• H ₀ : μ = 15 (実際の母集団平均は 15 インチに等しい)
• H ₁ : μ ≠ 15 (真の母集団平均は 15 インチに等しくない)

α = 0.05 の有意水準を使用します。

ステップ 1: 1 サンプルの t 検定オプションを選択します。

[分析]タブをクリックし、 [平均の比較] 、 [1 サンプル T 検定]の順にクリックします。

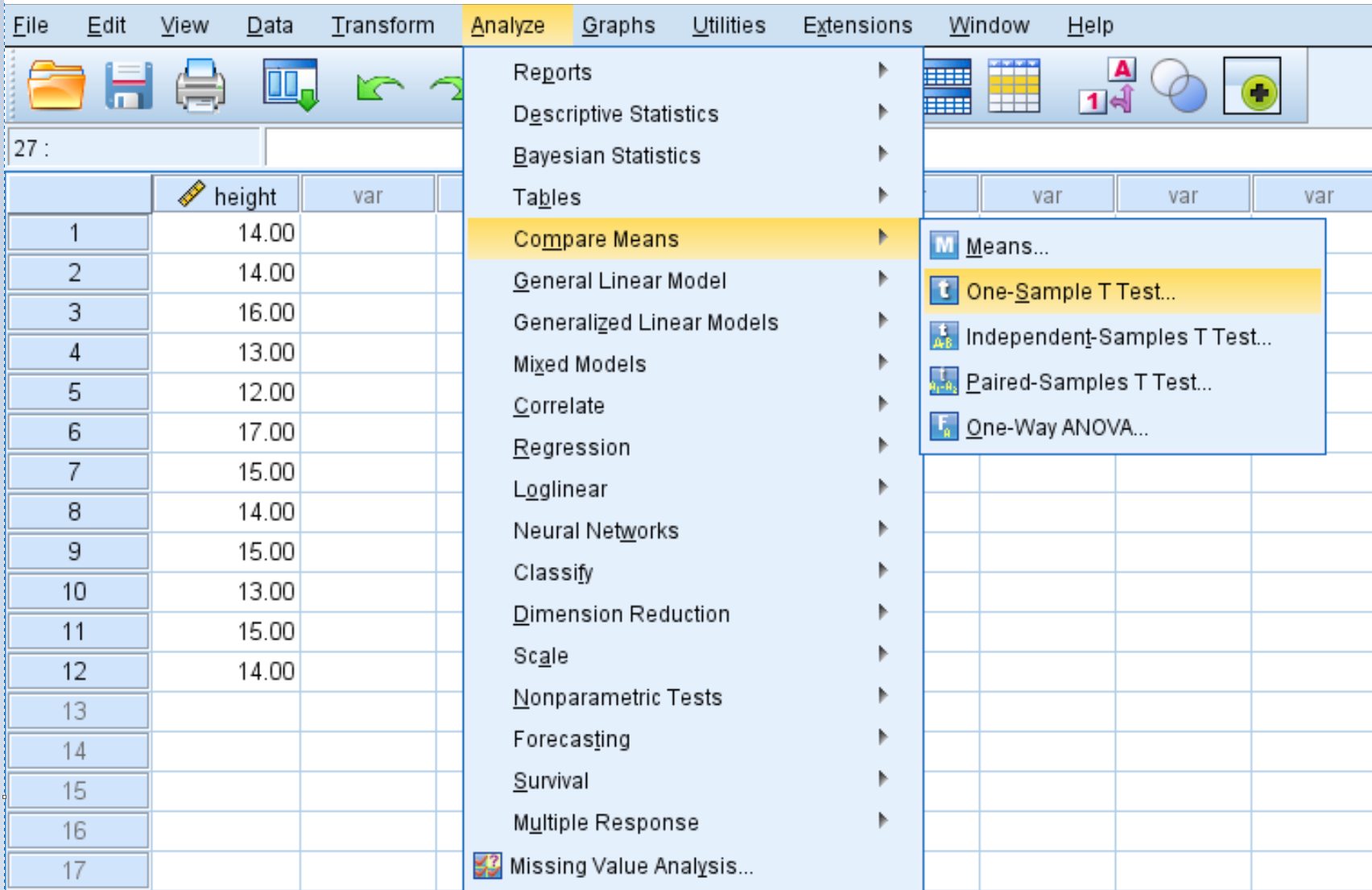
ステップ 2: 1 サンプルの t 検定を実行するために必要な値を入力します。

[One-Sample T Test]をクリックすると、次のウィンドウが表示されます。

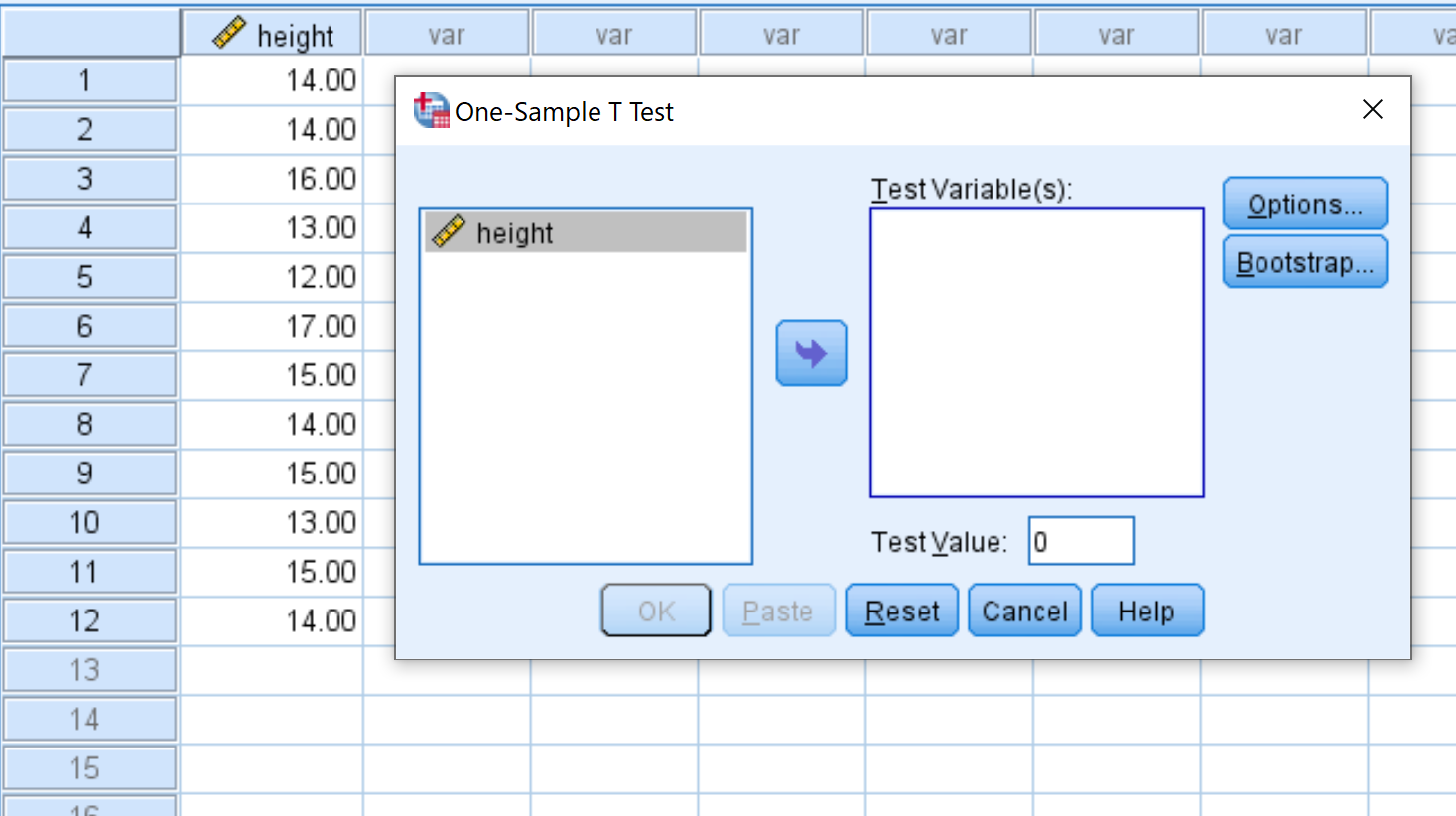
変数の高さを「テスト変数」というラベルのボックスにドラッグし、 「テスト値」を 15 に変更します。次に、 「OK」をクリックします。

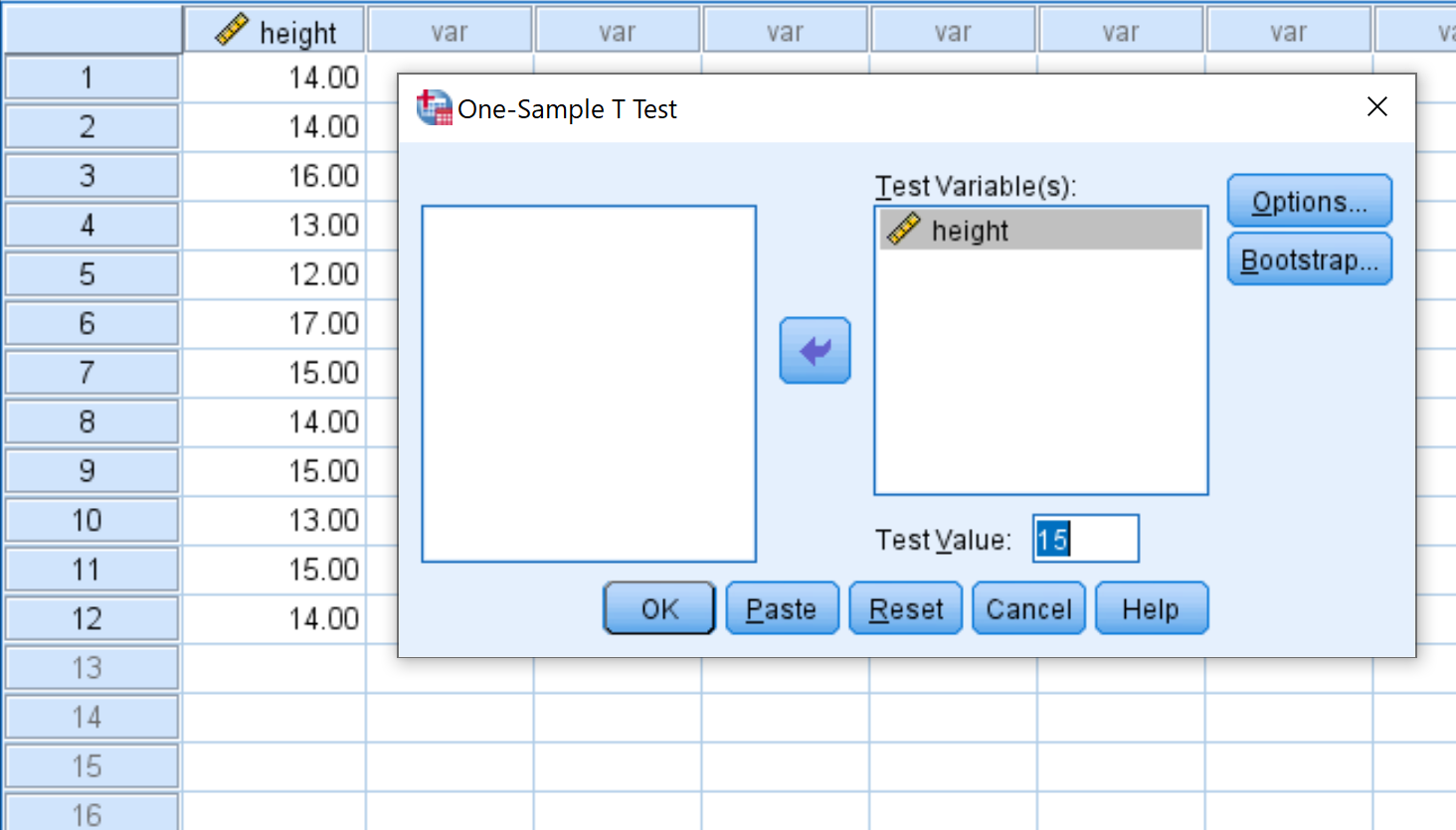
ステップ 3: 結果を解釈します。

[OK]をクリックすると、1 サンプルの t 検定の結果が表示されます。

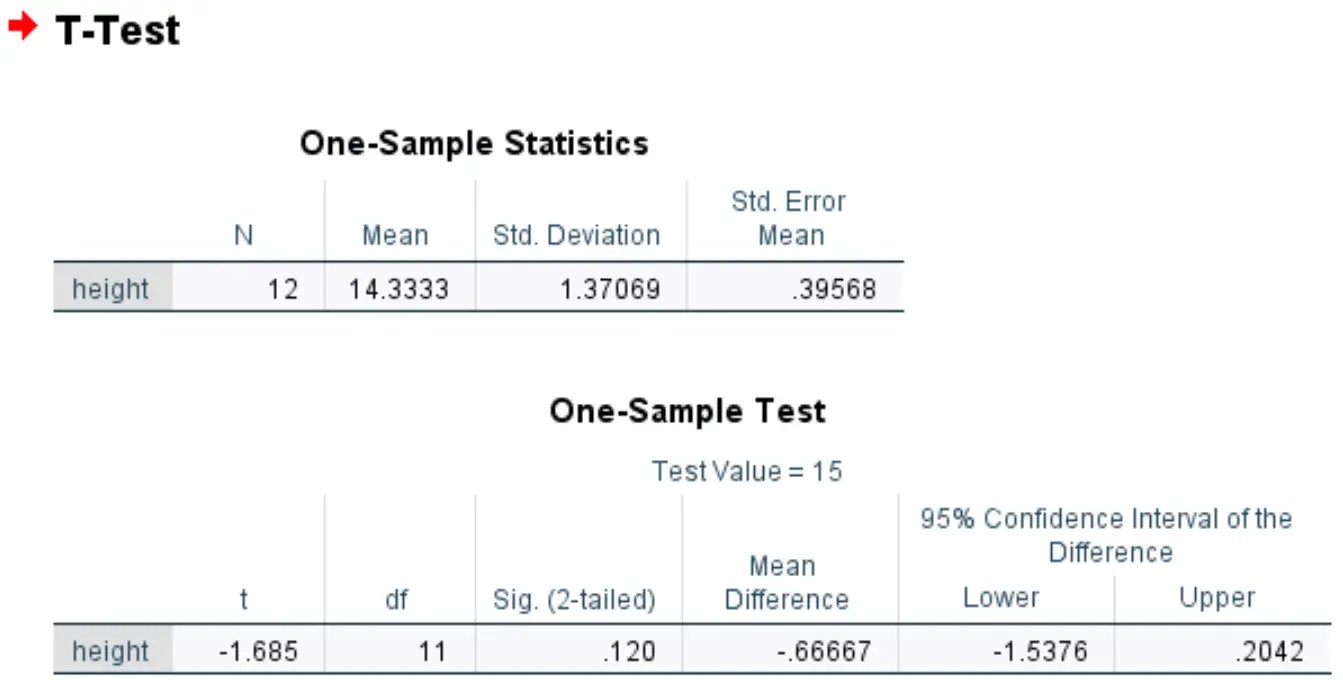
最初の表には、可変高さの要約統計が表示されます。

• N:サンプルサイズ
• 平均:サンプル内の植物の平均高さ
• 標準。偏差:サンプル内の植物の高さの標準偏差。
• 標準。平均誤差:平均の標準誤差。s/√n として計算されます。

2 番目の表には、1 サンプルの t 検定の結果が表示されます。

• t:検定統計量。(x – μ) / (s/√n) = (14.3333-15) / (1.37/√12) = -1.685 として計算されます。
• df:自由度、n-1 = 12-1 = 11 として計算されます。
• シグ。 (両側): df=11 の値 -1.685 に対応する両側 p 値
• 平均差:サンプル平均と仮説平均の差
• 95% CI 差:サンプル平均と仮説平均の間の真の差の 95%信頼区間。

検定の p 値 (0.120) は 0.05 未満ではないため、帰無仮説を棄却できません。この植物種の真の平均高さが 15 インチ以外であると言える十分な証拠はありません。