Stata で 1 サンプルの t 検定を実行する方法

1 サンプル t 検定は、母集団の平均が特定の値に等しいかどうかを検定するために使用されます。

このチュートリアルでは、Stata で 1 サンプルの t 検定を実行する方法を説明します。

例: Stata での 1 サンプルの t 検定

研究者たちは、自動車が 1 ガロンあたり平均 20 マイル走行するかどうかを知りたいと考えています。彼らは 74 台の車のサンプルを収集し、サンプル T 検定を実行して、真の平均 mpg が 20 であるかどうかを判断したいと考えています。

1 サンプルの t 検定を実行するには、次の手順を実行します。

ステップ 1: データをロードします。

まず、コマンド ボックスにuse https://www.stata-press.com/data/r13/autoと入力し、Enter をクリックしてデータをロードします。

ステップ2: 生データを表示します。

1 サンプルの t 検定を実行する前に、まず生データを見てみましょう。上部のメニュー バーから、 [データ] > [データ エディター] > [データ エディター (参照)]に移動します。これにより、74 台の各車に関する大量の情報が表示されますが、関心があるのはガロンあたりのマイル数 ( mpg列) だけであることに注意してください。

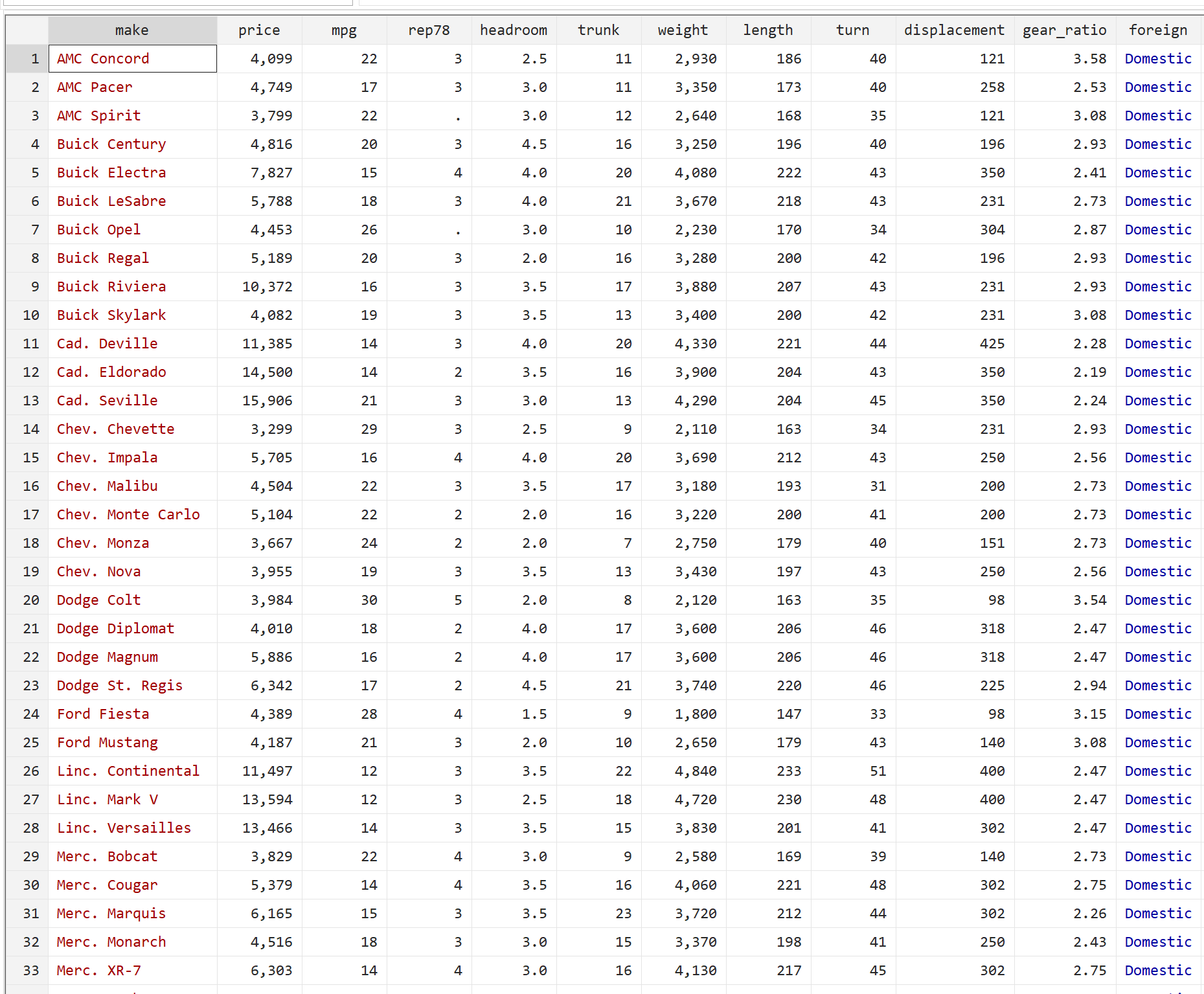
ステップ 3: 1 サンプルの t 検定を実行します。

上部のメニュー バーから、 [統計] > [要約、表および検定] > [従来の仮説検定] > [t 検定 (平均値検定の比較)]に移動します。

選択したサンプルを保存します。 [変数名] として、 mpgを選択します。 [仮説の平均] に20と入力します。 [信頼レベル] で、必要なレベルを選択します。値 95 は、有意水準 0.05 に対応します。これは 95 のままにしておきます。最後に、 [OK]をクリックします。

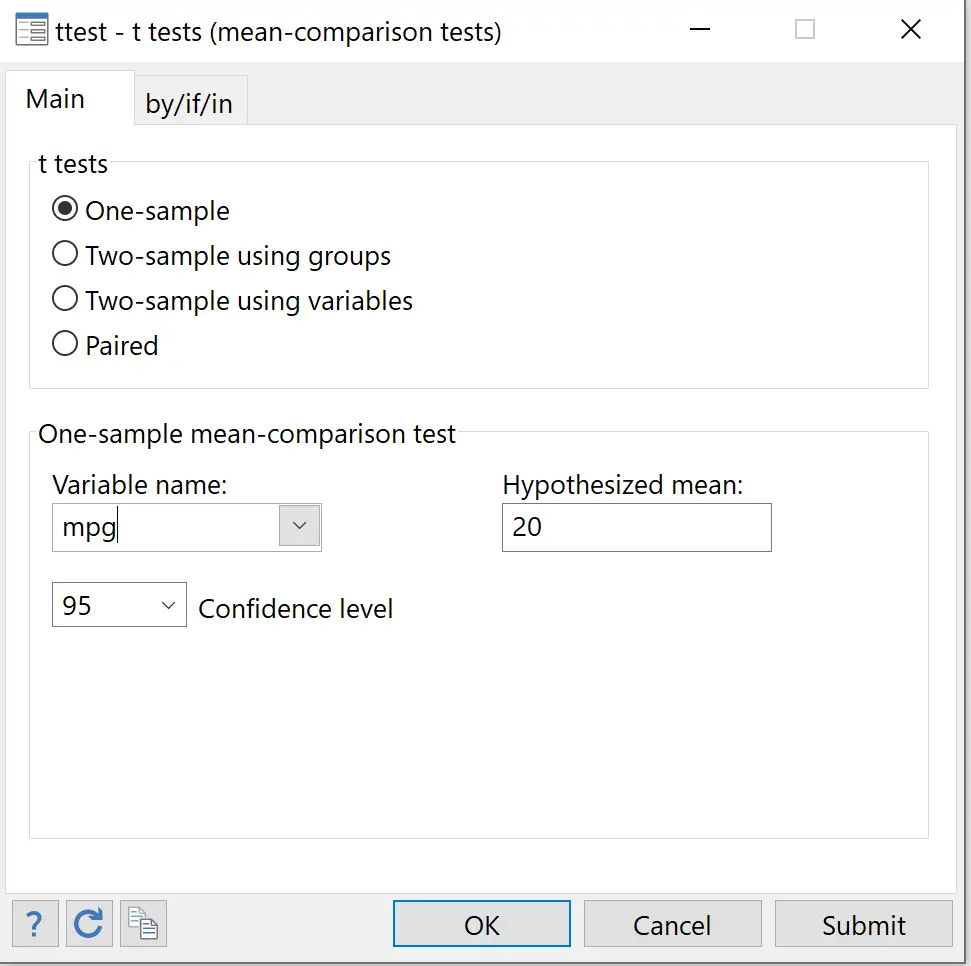
1 サンプルの t 検定の結果が表示されます。

結果を解釈する方法は次のとおりです。

Obs:観測値の数。この場合、車両は合計 74 台になります。

平均:すべての車の平均 mpg。この場合、平均は 1 ガロンあたり 21.2973 マイルです。

標準。エラー: σ / √ n = 5.785503 / √ 74 = 0.6725511 として計算されます。

標準。 Dev: mpg の標準偏差。この場合は 5.785503 です。

95％の確信区間:真の母集団平均に対する 95% 信頼区間。

t:検定統計量。(x – u) / (σ / √n ) = (21.2973-20) / 5.785503 / √74 = 1.9289 として計算されます。

自由度: t 検定に使用する自由度。n-1 = 74-1 = 73 として計算されます。

3 つの異なる 1 サンプル t 検定の p 値が結果の下部に表示されます。真の平均 mpg が 20 であるかどうかを理解したいため、p 値が0.0576である中間検定 (対立仮説は Ha: Average !=20) の結果を確認します。

この値は有意水準 0.05 を下回っていないため、帰無仮説を棄却できません。この車両群の真の平均燃費が 20 mpg 以外であると言える十分な証拠はありません。

ステップ 4: 結果を報告します。

最後に、1 サンプルの t 検定の結果を報告します。これを行う方法の例を次に示します。

74 台の車に対して 1 サンプルの t 検定を実行し、実際の母集団平均 mpg が 20 mpg と異なるかどうかを判定しました。

結果は、実際の母集団の平均値は、有意水準 0.05 で 20 mpg (t = 1.9289、df = 73、p = 0.0576) と変わらないことを示しました。

真の母集団平均に対する 95% 信頼区間は (19.9569, 22.63769) の区間となりました。