完全なガイド: 2×2 要因計画
2 × 2 要因計画は、研究者が 2 つの独立変数 (それぞれ 2水準) が 1 つの従属変数に及ぼす影響を理解できるようにする実験計画法の一種です。
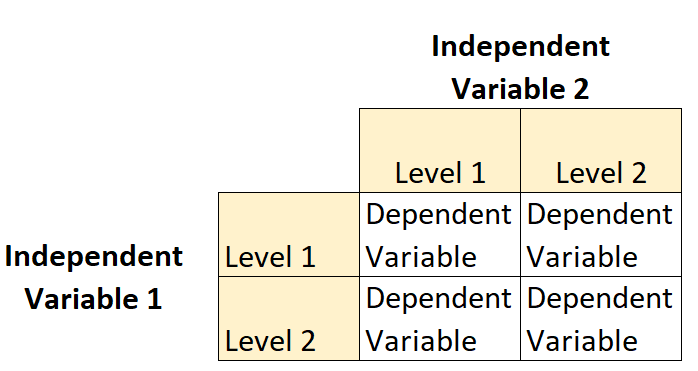
たとえば、植物学者が特定の植物種の成長に対する太陽光 (弱いまたは高い) と水やりの頻度 (毎日または毎週) の影響を理解したいとします。
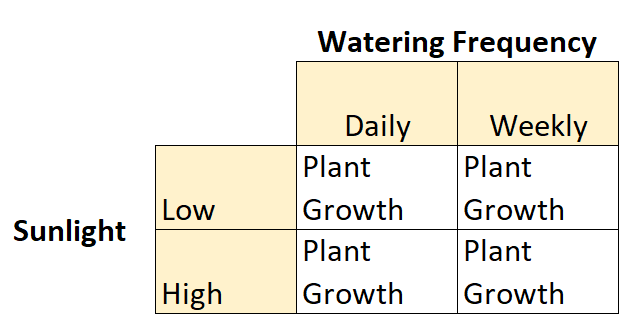
これは 2×2 要因計画の例です。これは、それぞれ 2 つのレベルを持つ 2 つの独立変数があるためです。
- 独立変数 #1:太陽光
- レベル:低、高
- 独立変数 #2:水やりの頻度
- レベル:毎日、毎週
そして、植物の成長という従属変数があります。
2×2要因計画の目的
2×2 要因計画では、次の効果を分析できます。
主効果:単一の独立変数が従属変数に及ぼす影響です。
たとえば、前のシナリオでは、次の主効果を分析できます。
- 植物の成長に対する太陽光の主な影響。
- 太陽の光が弱かったすべての植物の平均成長を見つけることができます。
- 強い日光を受けたすべての植物の平均成長を見つけることができます。
- 水やりの頻度が植物の成長に及ぼす主な影響。
- 毎日水を与えられたすべての植物の平均成長を見つけることができます。
- 毎週水を与えられたすべての植物の平均成長を見つけることができます。
交互作用効果: 1 つの独立変数の従属変数に対する効果が、他の独立変数の水準に依存する場合に発生します。
たとえば、前のシナリオでは、次の相互作用効果を分析できます。
- 植物の成長に対する太陽光の影響は水やりの頻度に依存しますか?
- 水やりの頻度が植物の成長に与える影響は太陽光に依存しますか?
主効果と交互作用効果を視覚化する
2 × 2 要因計画を使用する場合、独立変数が従属変数に及ぼす影響をよりよく理解するために平均をグラフ化することがよくあります。
たとえば、次のプロットを考えてみましょう。
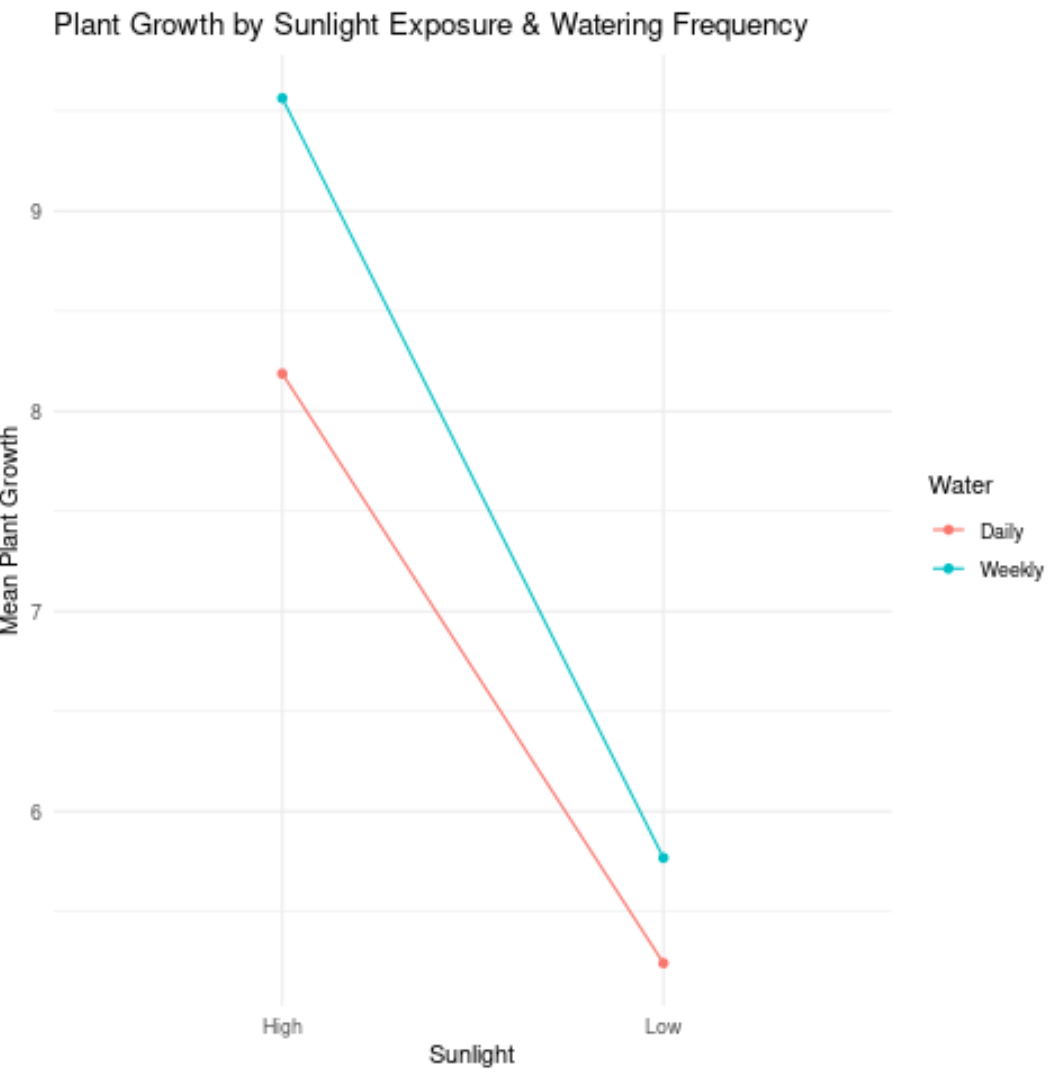
プロット内の値を解釈する方法は次のとおりです。
- 強い日光と毎日の水やりを受けた植物の平均成長は約8.2インチでした。
- 強い日光と毎週の水やりを受けた植物の平均成長は約9.6インチでした。
- 太陽が低く、毎日水やりを受けた植物の平均成長は約5.3インチでした。
- 太陽が低く、毎週水やりを受けた植物の平均成長は約5.8インチでした。
2 つの独立変数間に相互作用効果があるかどうかを判断するには、線が平行かどうかを確認するだけです。
- プロットの 2 つの線が平行である場合、交互作用効果はありません。
- プロットの 2 つの線が平行でない場合は、交互作用効果が存在します。
前のグラフでは、2 つの線はほぼ平行であったため、おそらく水やりの頻度と日光曝露の間に相互作用効果はありません。
ただし、次のプロットを考えてみましょう。
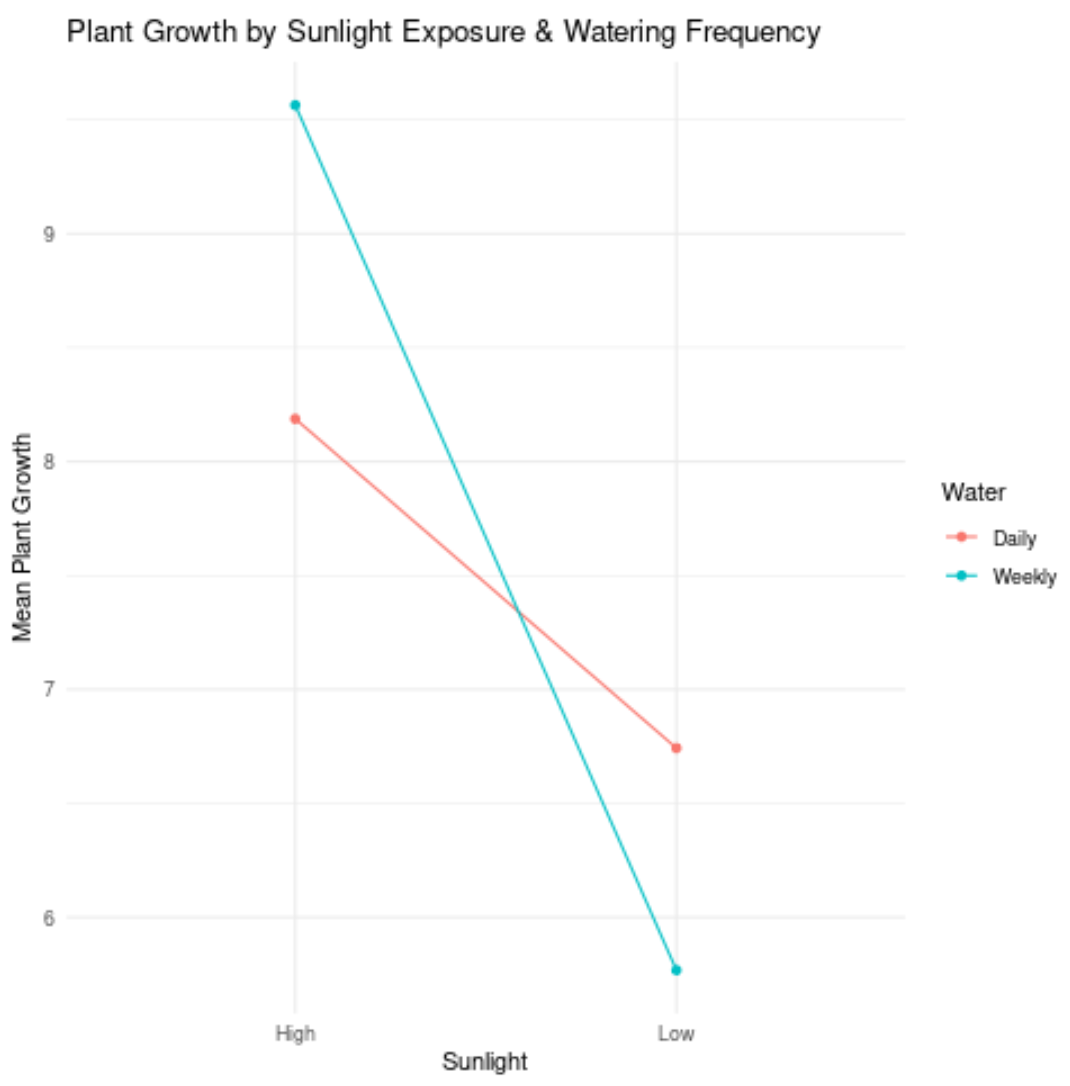
2 つの線はまったく平行ではありません (実際には交差しています!)。これは、おそらくそれらの間に相互作用効果があることを示しています。
たとえば、これは、植物の成長に対する太陽光の影響が水やりの頻度に依存することを意味します。
言い換えれば、日光と水やりの頻度は独立して植物の成長に影響を与えるわけではありません。むしろ、2 つの独立変数の間には交互作用効果があります。
2×2要因計画を分析する方法
平均をプロットすることは、独立変数が従属変数に与える影響を視覚的に検査する方法です。
ただし、二元配置分散分析を実行して、独立変数が従属変数と統計的に有意な関係があるかどうかを正式にテストすることもできます。
たとえば、次のコードは、R での仮想の工場シナリオに対して二元配置分散分析を実行する方法を示しています。
#make this example reproducible set. seeds (0) df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ), water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ), growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2), rnorm(15, 10, 3))) #fit the two-way ANOVA model model <- aov(growth ~ sunlight * water, data = df) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) sunlight 1 52.5 52.48 8.440 0.00525 ** water 1 31.6 31.59 5.081 0.02813 * sunlight:water 1 12.8 12.85 2.066 0.15620 Residuals 56 348.2 6.22 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
ANOVA 結果を解釈する方法は次のとおりです。
- 太陽光に関連する p 値は0.005です。この数値は 0.05 未満であるため、太陽光への曝露が植物の成長に統計的に有意な影響を与えていることを意味します。
- 水に関連する p 値は0.028です。この数値は 0.05 未満であるため、水やりの頻度も植物の成長に統計的に有意な影響を与えることを意味します。
- 太陽光と水の間の相互作用の p 値は0.156です。この数値は0.05以上なので、太陽光と水の相互作用効果がないことを意味します。