完全なガイド: 2×4 要因計画

2 × 4 要因計画は、研究者が 1 つの従属変数に対する 2 つの独立変数の影響を理解できるようにする実験計画法の一種です。

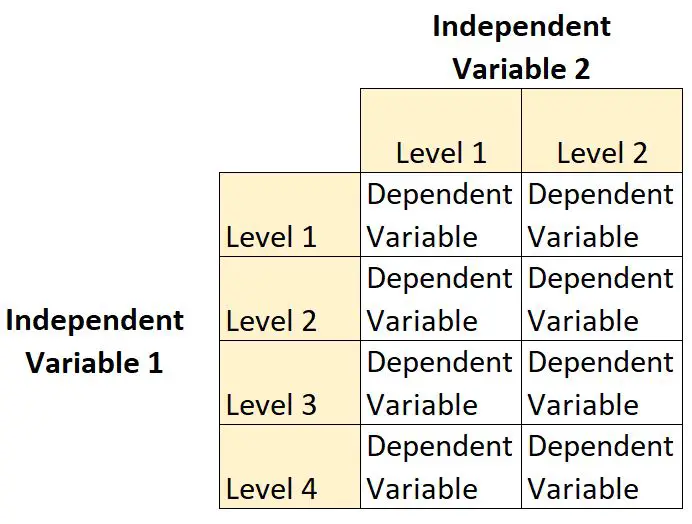
このタイプの計画では、1 つの独立変数には 2水準があり、もう 1 つの独立変数には 4 水準があります。

たとえば、植物学者が、特定の植物種の成長に対する太陽光 (なし、弱、中、または強) と水やりの頻度 (毎日または毎週) の影響を理解したいとします。

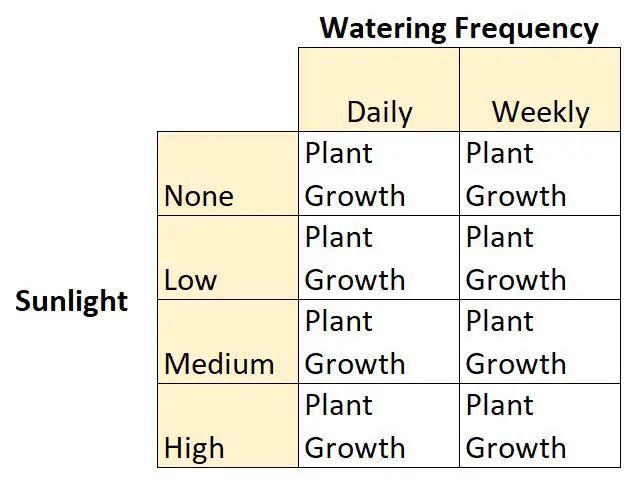
これは 2 × 4 要因計画の例です。これは、2 つの独立変数 (1 つは 2 水準、もう 1 つは 4 水準) があるためです。

• 独立変数 #1:太陽光
  • レベル:なし、低、中、高
• 独立変数 #2:水やりの頻度
  • レベル:毎日、毎週

そして、植物の成長という従属変数があります。

2×4要因計画の目的

2×4 要因計画では、次の効果を分析できます。

主効果:単一の独立変数が従属変数に及ぼす影響です。

たとえば、前のシナリオでは、次の主効果を分析できます。

• 植物の成長に対する太陽光の主な影響。
  • 日光を受けなかったすべての植物の平均成長。
  • 弱い日光を受けたすべての植物の平均成長。
  • 平均的な太陽光を受けたすべての植物の平均的な成長。
  • 強い日光を受けたすべての植物の平均成長。
• 水やりの頻度が植物の成長に及ぼす主な影響。
  • 毎日水を与えられたすべての植物の平均成長。
  • 毎週水を与えられたすべての植物の平均成長。

交互作用効果: 1 つの独立変数の従属変数に対する効果が、他の独立変数の水準に依存する場合に発生します。

たとえば、前のシナリオでは、次の相互作用効果を分析できます。

• 植物の成長に対する太陽光の影響は水やりの頻度に依存しますか?
• 水やりの頻度が植物の成長に与える影響は太陽光に依存しますか？

2×4要因計画を分析する方法

二元配置分散分析を実行して、独立変数が従属変数と統計的に有意な関係があるかどうかを正式にテストできます。

たとえば、次のコードは、R での仮想の工場シナリオに対して二元配置分散分析を実行する方法を示しています。

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' None ', ' Low ', ' Medium ', ' High '), each= 10 , times= 2 ),
                 water = rep(c(' Daily ', ' Weekly '), each= 40 , times= 2 ),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 3 744.1 248.04 34.16 < 2e-16 ***
water 1 43.1 43.05 5.93 0.016 *  
sunlight:water 3 195.8 65.27 8.99 1.61e-05 ***
Residuals 152 1103.5 7.26                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ANOVA 結果を解釈する方法は次のとおりです。

主効果 #1 (太陽光) : 太陽光に関連する p 値は<2e-16です。この数値は 0.05 未満であるため、太陽光への曝露が植物の成長に統計的に有意な影響を与えていることを意味します。

主効果 #2 (水) : 水に関連する p 値は0.016です。この数値は 0.05 未満であるため、水やりの頻度も植物の成長に統計的に有意な影響を与えることを意味します。

相互作用効果: 太陽光と水の間の相互作用の p 値は0.000061です。この値は 0.05 未満であるため、太陽光と水の間に相互作用効果があることを意味します。

追加リソース

次のチュートリアルでは、実験計画と分析に関する追加情報を提供します。

完全なガイド: 2 × 2 要因計画
完全なガイド: 2 × 3 要因計画
階乗分散分析とは何ですか?