集計バイアスとは何ですか? (説明と例)
集計バイアスは、集計データで観察された傾向が個々のデータ ポイントにも当てはまると誤って想定される場合に発生します。
この種のバイアスを理解する最も簡単な方法は、簡単な例を挙げることです。
例: 集計バイアス
研究者が、特定の州における平均教育年数と平均世帯収入との関係を理解したいとします。彼らは州内の 4 つの異なる都市の集計データを取得し、平均教育と平均世帯収入の間の相関関係を計算しました。
平均教育年数と平均世帯収入との相関関係は0.9632であることがわかります。これは非常に正の相関係数です。
研究者は、平均教育年数と平均世帯収入の関係を視覚化するための散布図も作成しています。
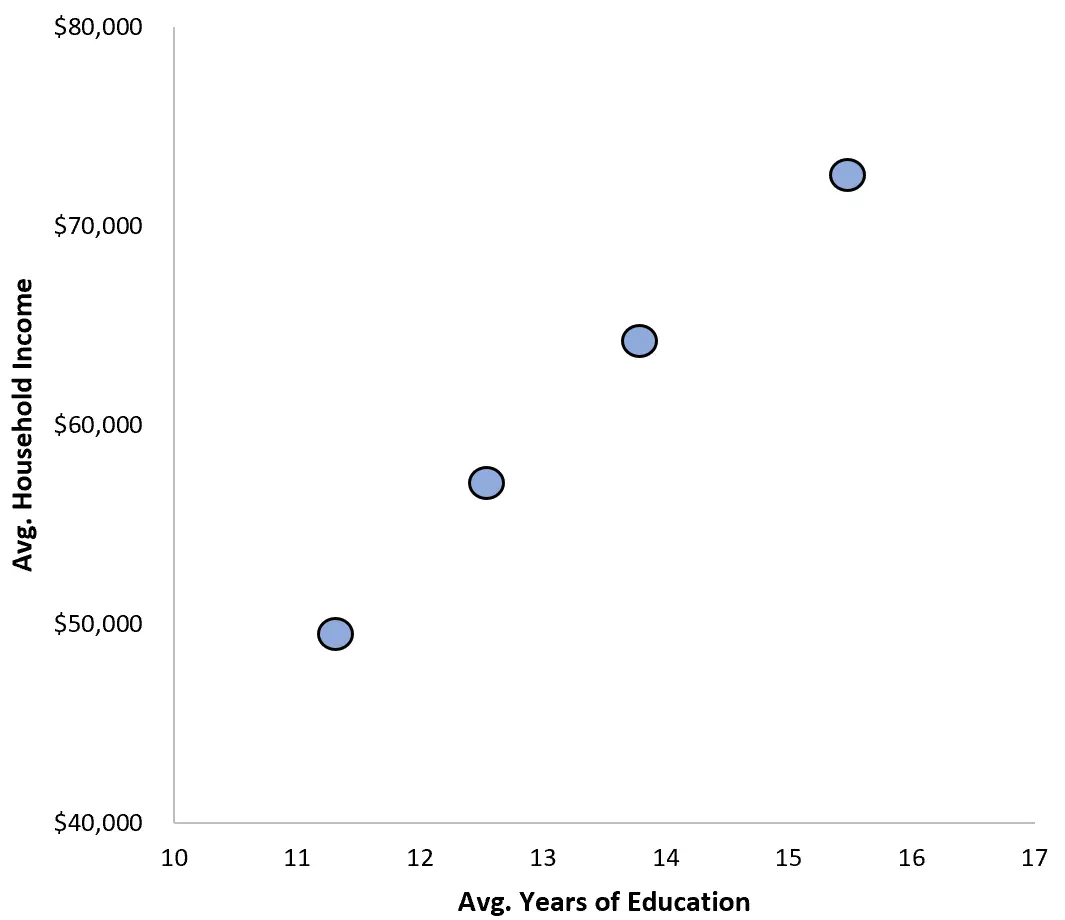
実際に個々のデータを調べずに、教育年数の増加が世帯収入と強い正の相関があると主張するレポートを発表することもできます。
しかし、1 年後に新しい研究者が来て、同じ一連の都市の個々の世帯に関するデータを入手したとします。彼女が次のようなデータの散布図を作成したとします。
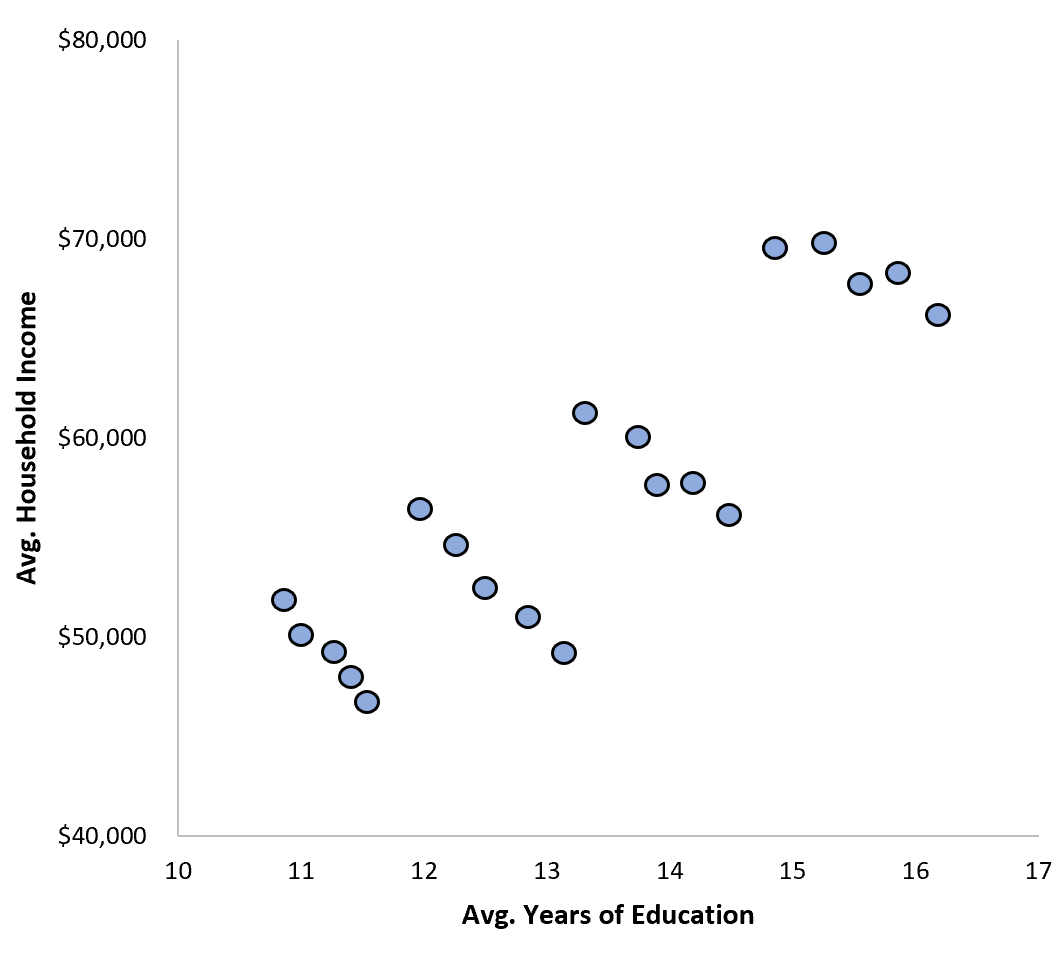
彼女は 2 つの変数間の相関関係を計算し、実際にはわずか0.1788であることがわかりました。それでも正の相関関係ではありますが、以前の研究者が発見した相関関係ほど強力ではありません。
データを集計すると、個人レベルで発生している教育と収入の間の真の傾向がカバーされていることがわかりました。
実際、散布図で都市ごとに見てみると、教育と収入の関係は実際には負の関係になっています。
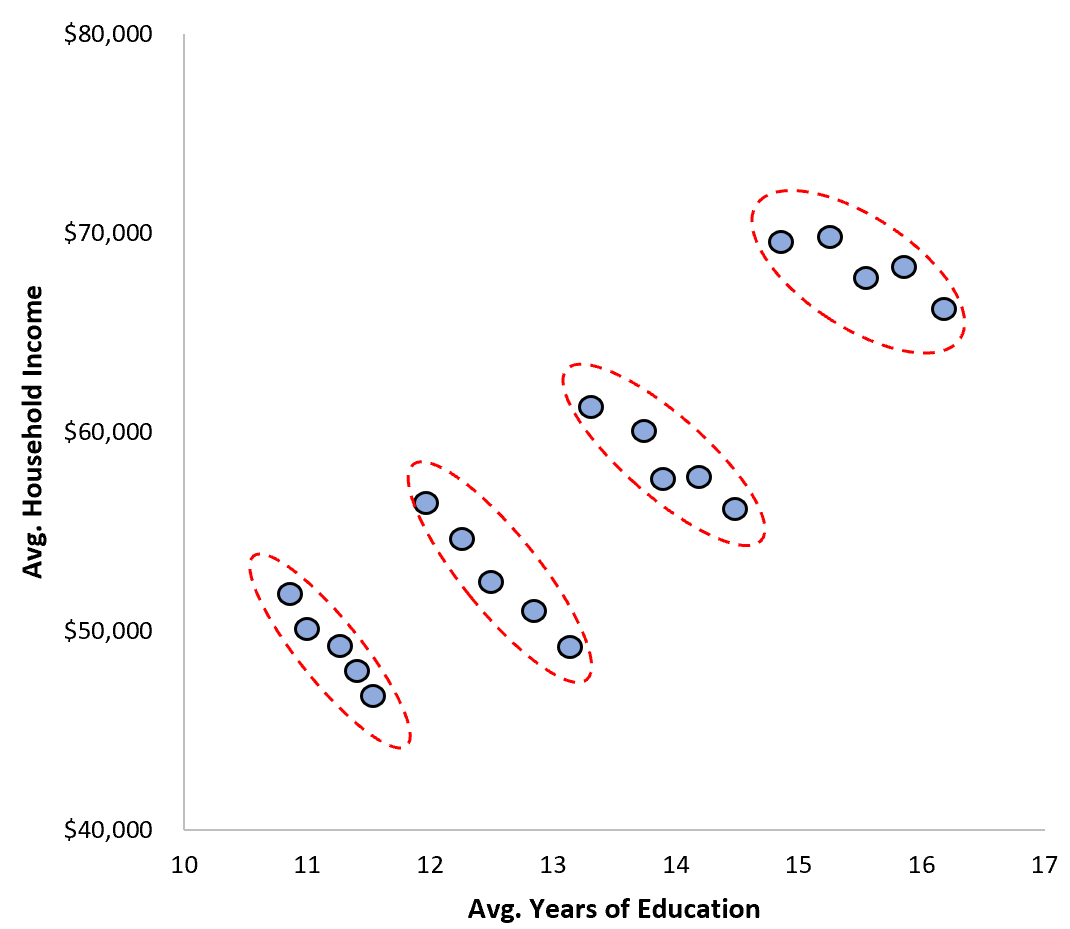
集計バイアスの影響
集計バイアスが研究で頻繁に発生するのは、集計レベルで現れる傾向が個人レベルでも現れるはずだと誤って想定されていることが多いためです。残念ながら、前の例が示すように、これは常に当てはまるわけではありません。
集計バイアスにより、研究結果が誤った結論を導き出し、誤解を招く可能性があります。このタイプのバイアスは、変数間の相関関係に関係する場合に特に有害です。
2 つの変数の集計データ間の相関関係が正の場合でも、個々の観測レベルでの 2 つの変数間の基礎的な相関関係は、実際には次のとおりである可能性があります。
- 負の相関
- 相関関係なし
- 正の相関
この種のバイアスを回避する方法は、データ ポイントを集計するのではなく、個々のデータ ポイントを使用して調査を実施し、2 つの変数間の真の関係を発見できるようにすることです。