ポアソン信頼区間を計算する方法 (ステップバイステップ)
ポアソン分布は、イベントが独立して一定の平均率で発生することがわかっている場合に、一定の時間間隔内に特定の数のイベントが発生する確率をモデル化するために使用される確率分布です。
ポアソン過程の平均発生数を知ることは役に立ちますが、平均発生数の周りに信頼区間があるとさらに役立つ場合があります。
たとえば、ランダムな日にコールセンターでデータを収集し、1 時間あたりの平均通話数が 15 件であることを確認したとします。
データを収集したのは 1 日分だけであるため、コールセンターが年間を通じて 1 時間あたり平均 15 件の電話を受けているとは確信できません。
ただし、次の式を使用して、1 時間あたりの平均コール数の信頼区間を計算できます。
ポアソン信頼区間の公式
信頼区間 = [0.5*X 2 2N, α/2 , 0.5*X 2 2(N+1), 1-α/2 ]
金:
- X 2 : カイ二乗の臨界値
- N: 観測されたイベントの数
- α: 重要度
次の段階的な例は、実際に 95% ポアソン信頼区間を計算する方法を示しています。
ステップ 1: 観察されたイベントを数える
コールセンターでの 1 時間あたりの平均通話数が 15 であると計算するとします。つまり、 N = 15 となります。
また、95% 信頼区間を計算しているため、次の計算ではα = 0.05を使用します。
ステップ 2: 信頼区間の下限を見つける
信頼区間の下限は次のように計算されます。
- 下限値 = 0.5*X 2 2N、α/2
- 下限 = 0.5*X 2 2(15)、0.975
- 下限 = 0.5*X 2 30、0.975
- 下限 = 0.5*16.791
- 下限 = 8.40
注: X 2 30, 0.975を計算するには 、カイ二乗臨界値計算ツールを使用しました。
ステップ 3: 信頼区間の上限を見つける
信頼区間の上限は次のように計算されます。
- 上限 = 0.5*X 2 2(N+1)、1-α/2
- 上限 = 0.5*X 2 2(15+1)、0.025
- 上限 = 0.5*X 2 32、0.025
- 上限 = 0.5*49.48
- 上限 = 24.74
注: X 2 32.0.025を計算するには 、カイ二乗臨界値計算ツールを使用しました。
ステップ 4: 信頼区間を求める
以前に計算した下限と上限を使用すると、95% ポアソン信頼区間は次のようになります。
- 95% CI = [8.40, 24.74]
これは、コールセンターが受け取る 1 時間あたりの実際の平均コール数が 8.40 コールから 24.74 コールの間にあると 95% の確率で確信できることを意味します。
ボーナス: 魚の信頼区間計算ツール
このポアソン信頼区間計算ツールを自由に使用して、ポアソン信頼区間を自動的に計算します。
たとえば、この計算ツールを使用して、手動で計算したポアソン信頼区間を見つける方法は次のとおりです。
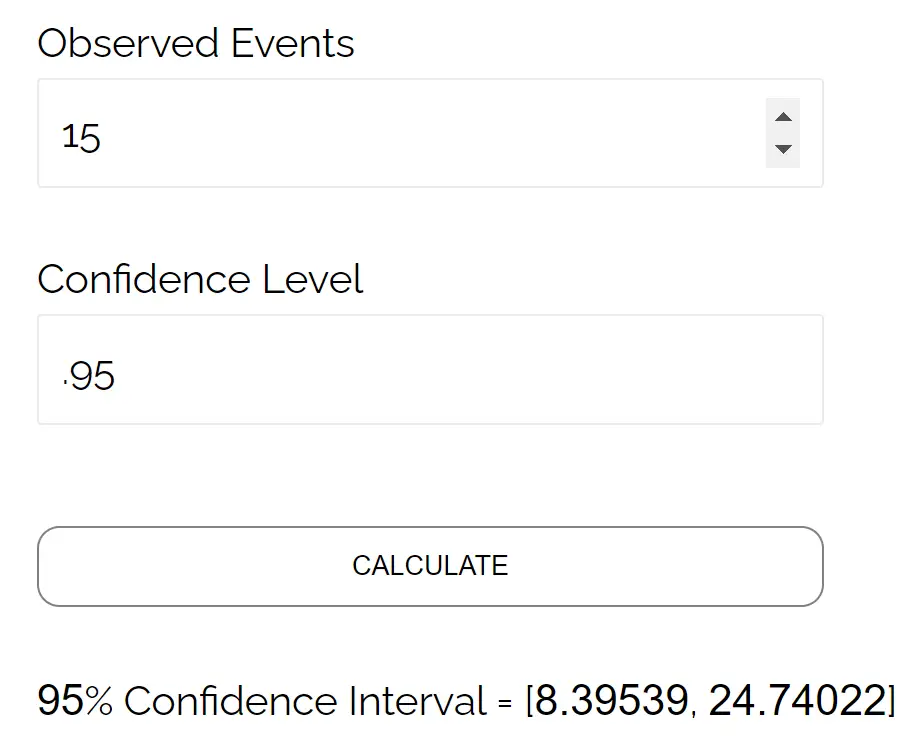
結果は手動で計算した信頼区間に対応していることに注意してください。