分散がマイナスになることはありますか?

統計学では、分散という用語は、特定のデータセット内で値がどのように分布しているかを指します。

分散に関する学生からのよくある質問は次のとおりです。

分散がマイナスになることはありますか?

答え:いいえ、分散を負にすることはできません。取り得る最小値はゼロです。

この理由を理解するには、分散が実際にどのように計算されるかを理解する必要があります。

ギャップの計算方法

サンプルの分散を求める式 ( s ²で示されます) は次のとおりです。

s ² = Σ (x _i – x ) ² / (n-1)

金：

• x : サンプルの意味
• x _i : サンプル内の^{i 番目の}観測値
• N : サンプルサイズ
• Σ : 「和」を意味するギリシャ語の記号

たとえば、10 個の値を含む次のデータセットがあるとします。

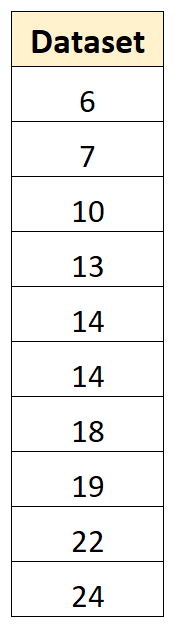
次の手順を使用して、このサンプルの分散を計算できます。

ステップ 1: 平均を見つける

平均はあくまで平均です。これは14.7であることがわかります。

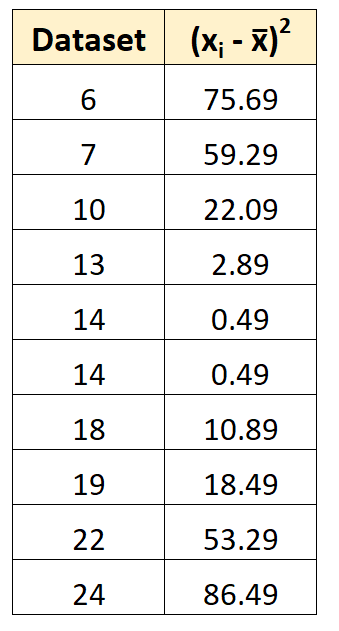
ステップ 2: 二乗偏差を求める

次に、平均からの個々の値の二乗偏差を計算できます。

たとえば、最初の二乗偏差は (6-14.7) ² = 75.69 として計算されます。

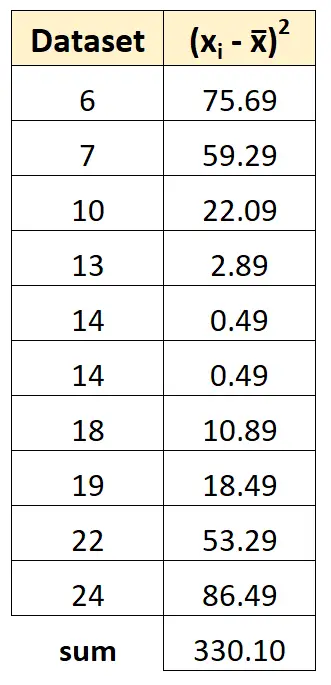
ステップ 3: 偏差の二乗の合計を求める

次に、偏差のすべての二乗を合計できます。

ステップ 4: 標本分散を計算する

最後に、標本の分散を、偏差の二乗和を (n-1) で割ったものとして計算できます。

s ² = 330.1 / (10-1) = 330.1 / 9 = 36.678

標本分散は36,678であることがわかります。

ゼロ分散の例

データセットの分散をゼロにする唯一の方法は、データセット内のすべての値が同じである場合です。

たとえば、次のデータセットの標本分散はゼロです。

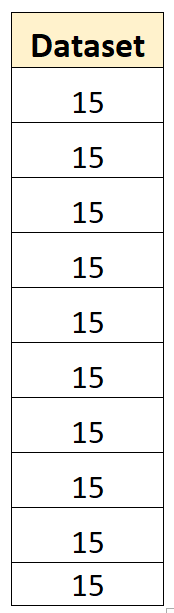
データセットの平均は 15 で、個々の値はいずれも平均から逸脱しません。したがって、偏差の二乗和はゼロになり、標本分散は単純にゼロになります。

標準偏差がマイナスになることはありますか?

データセット内の値の分布を測定するより一般的な方法は、分散の平方根である標準偏差を使用することです。

たとえば、特定のサンプルの分散が^s2 = 36.678の場合、標準偏差 ( sと表記) は次のように計算されます。

s = √ ^s2 = √ 36.678 = 6.056

分散が常にゼロまたは正の数であることはすでにわかっているため、ゼロまたは正の数の平方根が負になることはないため、標準偏差が負になることはあり得ないことを意味します。

追加リソース

中心傾向の尺度: 定義と例
分散対策: 定義と例