正規分布または一様分布: 違いは何ですか?
正規分布は、統計で最もよく使用される確率分布です。
次のような特性があります。
- 対称
- ベル型
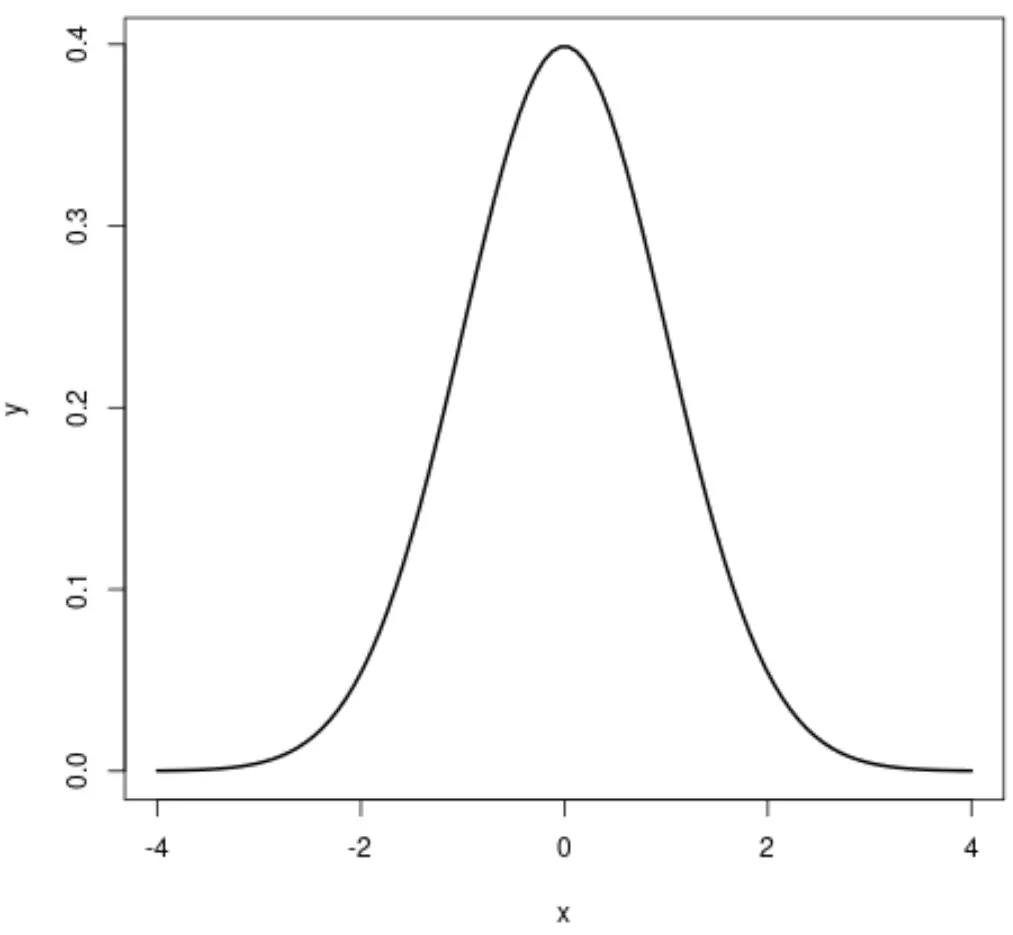
正規分布のプロットを作成すると、次のようになります。
一様分布とは、 aからbまでの区間の間の各値が同じ確率で出現する確率分布です。
次のような特性があります。
- 対称
- 長方形の形状
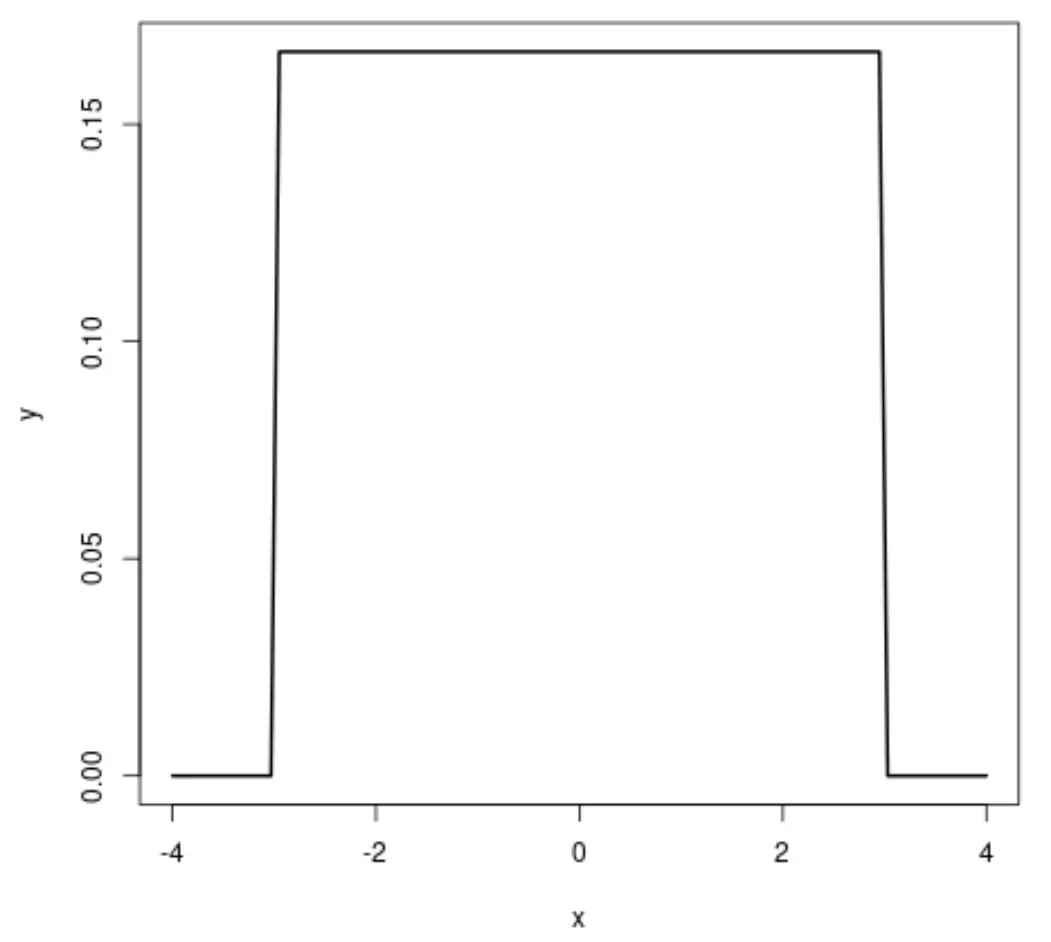
一様分布のプロットを作成すると、次のようになります。
正規分布と一様分布には次の類似点があります。
- 2 つの分布は対称です。つまり、分布の中心を通る線を引くと、分布の左側と右側は完全に鏡映し合うことになります。
ただし、2 つのディストリビューションには次のような違いがあります。
- 分布にはさまざまな形があります。
- 正規分布は釣鐘型です。これは、分布の中心付近の値が分布の末尾の値よりも発生する可能性が高いことを意味します。
- 一様分布は長方形の形状をしています。これは、分布内の各値の発生確率が同じであることを意味します。
正規分布または一様分布: いつ使用するか?
正規分布は、 「釣鐘曲線」形状に従う傾向がある現象をモデル化するために使用されます。たとえば、新生児の出生体重は通常、平均して約 7.5 ポンドに分布していることが十分に文書化されています。
米国の新生児の出生体重のヒストグラムは、一般に正規分布に対応する釣鐘型を示しています。

ほとんどの赤ちゃんの体重はおそらく 7.5 ポンド前後ですが、7 ポンド未満の赤ちゃんも少数、8 ポンドを超える赤ちゃんもいます。
逆に、一様分布は、各潜在的な結果の可能性が等しいシナリオをモデル化するために使用されます。
典型的な例はサイコロを振ることです。サイコロを 1 回振ると、各数字の出現確率は同じであるため、1 ~ 6 の数字に当たる確率は一様分布に従います。
たとえば、サイコロが出る可能性のある数字は 6 つあるため、1 が出る確率は 1/6 です。
同様に、2 が出る確率は 1/6 です。
同様に、3 の目を出す確率は 1/6 です。
等々。
ボーナス: 正規分布と一様分布をプロットする方法
R で次のコードを使用して、正規分布と一様分布のプロットを作成しました。
#define x-axis x <- seq(-4, 4, length=100) #calculate normal distribution probabilities y <- dnorm(x) #plot normal distribution plot(x, y, type = " l ", lwd = 2 ) #define x-axis x <- seq(-4, 4, length=100) #calculate uniform distribution probabilities y <- dunif(x, min = -3, max = 3) #plot uniform distribution plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))