相関関係を使用する必要があるのはどのような場合ですか? (説明と例)
相関関係は、2 つの変数間の線形関連性を測定するために使用されます。
相関係数は常に -1 から 1 までの値を取ります。
- -1 は、2 つの変数間の完全な負の線形相関を示します。
- 0 は 2 つの変数間に線形相関がないことを示します
- 1 は、2 つの変数間の完全な正の線形相関を示します。
学生がよく尋ねる質問は、「相関関係をいつ使用する必要があるか?」です。
簡単な答え: 2 つの変数間の線形関係を定量化したい場合で、どちらの変数も応答変数または「結果」変数を表さない場合は、相関関係を使用します。
次の例は、実際に相関関係を使用すべき場合と使用すべきでない場合を示しています。
例 1: 相関関係を使用する場合
教授が、クラスの生徒の数学のテストの得点と科学のテストの得点の間の線形関係を理解したいとします。
たとえば、数学の試験で良い成績を収めた生徒は、科学の試験でも良い成績を収めますか?それとも、数学の得点が高い生徒は科学の得点が低い傾向にあるのでしょうか?
このシナリオでは、数学の試験の得点と科学の試験の得点の間の相関関係を計算できます。これは、2 つの変数間の線形関係を理解したいだけであり、どちらの変数も応答変数と見なすことはできないためです。
ピアソン相関係数を計算し、r = 0.78 であることが判明したとします。これは強い正の相関関係であり、数学で良い成績を収めた生徒は科学でも良い成績を収める傾向があることを意味します。
例 2: 相関関係を使用しない場合
企業のマーケティング部門が総収益に対する広告費の影響を定量化したいと考えているとします。
たとえば、広告に追加の 1 ドルを費やすごとに、企業はどのくらいの追加収益を得ることが期待できるでしょうか?
このシナリオでは、「収益」変数が応答変数であるため、部門は線形回帰モデルを使用して広告支出と総収益の関係を定量化する必要があります。
この部門が単純な線形回帰モデルを適用し、次の方程式が広告支出と総収益の関係を最もよく表していることを発見したとします。
総収益 = 145.4 + 0.34*(広告費)
これは、広告に追加の 1 ドルを費やすごとに総収益が平均 0.34 ドル増加することを意味すると解釈します。
相関使用時の注意事項
相関関係は 2 つの変数間の線形関係を定量化するためにのみ使用できることに注意することが重要です。
ただし、特定の状況では、相関係数は非線形関係を共有する 2 つの変数間の関係を効果的に捉えることができません。
たとえば、2 つの変数間の関係を視覚化するために次の散布図を作成するとします。
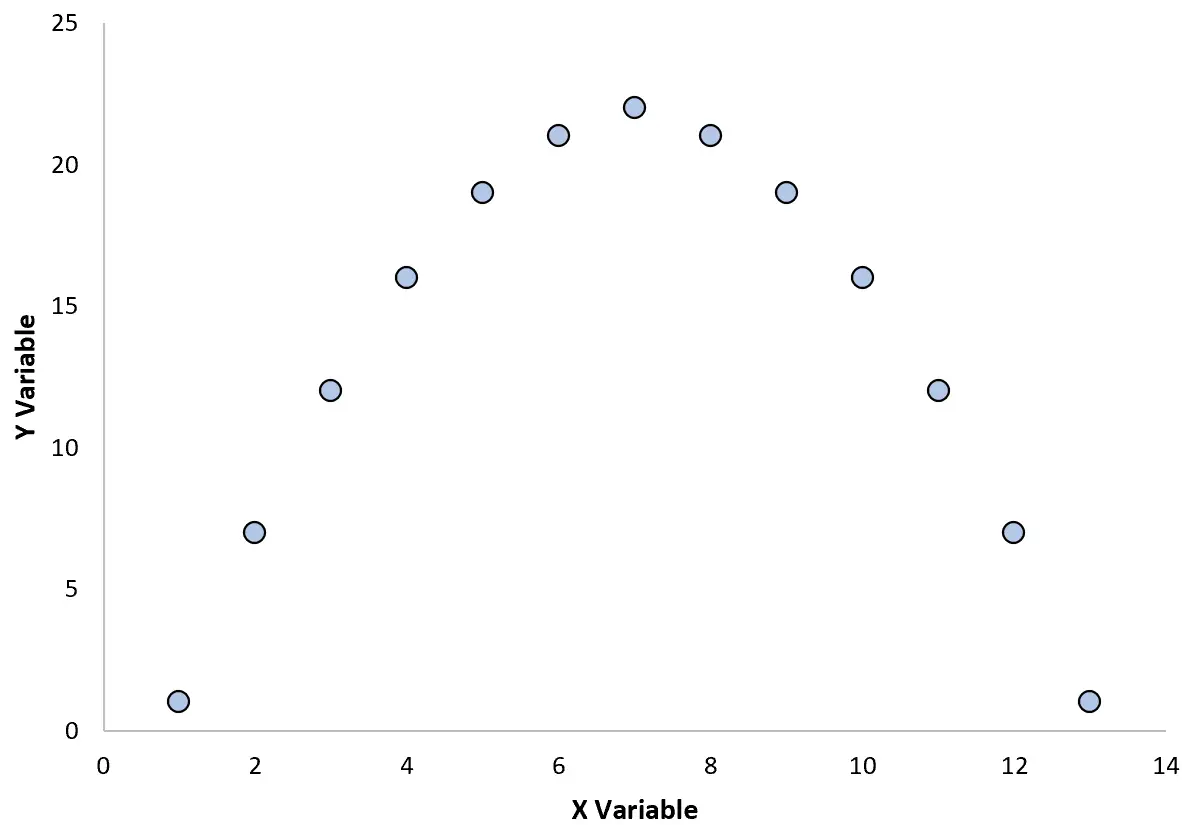
これら 2 つの変数間の相関係数を計算すると、r = 0 であることがわかります。これは、2 つの変数間に線形関係がないことを意味します。
ただし、グラフから、2 つの変数には実際に関係があることがわかります。これは、線形の関係ではなく、単に二次の関係です。
したがって、2 つの変数間の相関関係を計算するときは、変数間の関係を視覚化するために散布図を作成すると便利な場合もあることに留意してください。
2 つの変数に線形関係がない場合でも、散布図で明らかになる非線形関係がある可能性があります。
追加リソース
次のチュートリアルでは、さまざまな状況で相関関係がどのように使用されるかについて詳しく説明します。
相関関係の実例 6 つ
「強い」相関関係とは何ですか?
相関関係 vs.協会:違いは何ですか?
相関と回帰: 違いは何ですか?