Roc 曲線を解釈する方法 (例あり)
ロジスティック回帰は、応答変数がバイナリの場合に回帰モデルを近似するために使用する統計手法です。ロジスティック回帰モデルがデータセットにどの程度適合しているかを評価するには、次の 2 つの指標を確認します。
- 感度:結果が実際に肯定的な場合に、モデルが観測値に対して肯定的な結果を予測する確率。
- 特異性:結果が実際には陰性である場合に、モデルが観測に対して陰性の結果を予測する確率。
これら 2 つの指標を視覚化する簡単な方法は、ロジスティック回帰モデルの感度と特異度を表示するグラフであるROC 曲線 を作成することです。
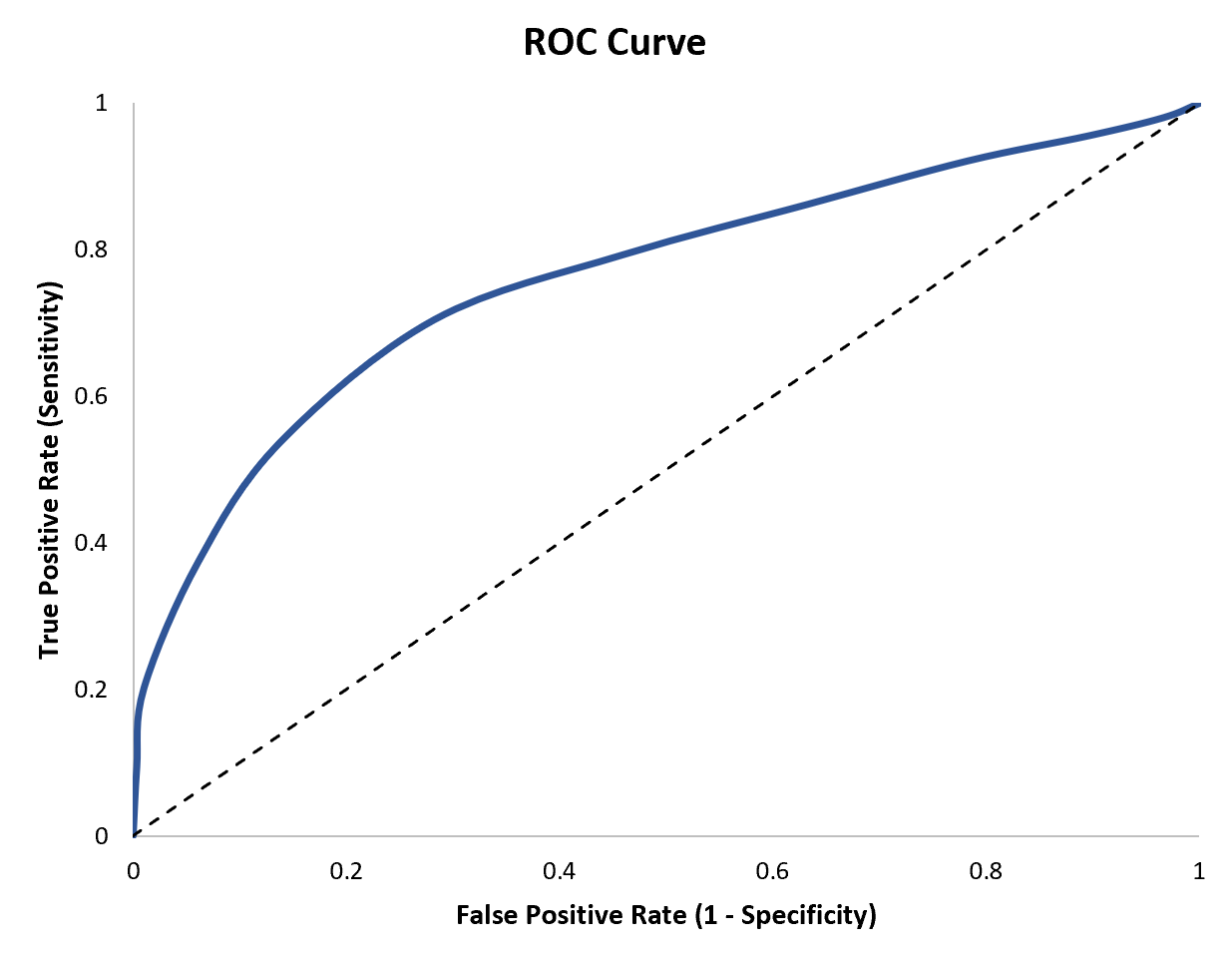
このチュートリアルでは、ROC 曲線を作成および解釈する方法を説明します。
ROC 曲線の作成方法
ロジスティック回帰モデルを適合させたら、そのモデルを使用して観測値を 2 つのカテゴリのいずれかに分類できます。
たとえば、観察を「ポジティブ」または「ネガティブ」に分類できます。
真陽性率は、実際には陽性であるはずの観測値の割合を表します。
逆に、偽陽性率は、陽性であるはずの観測値が実際には陰性である割合を表します。
ROC 曲線を作成するときは、ロジスティック回帰モデルの考えられる判定しきい値ごとに、真陽性率と偽陽性率のペアをプロットします。
ROC 曲線を解釈する方法
ROC 曲線がプロットの左上隅に近ければ近いほど、モデルはデータをより適切にカテゴリに分類できます。
これを定量化するには、プロットのどの程度が曲線の下にあるかを示すAUC (曲線下面積) を計算します。
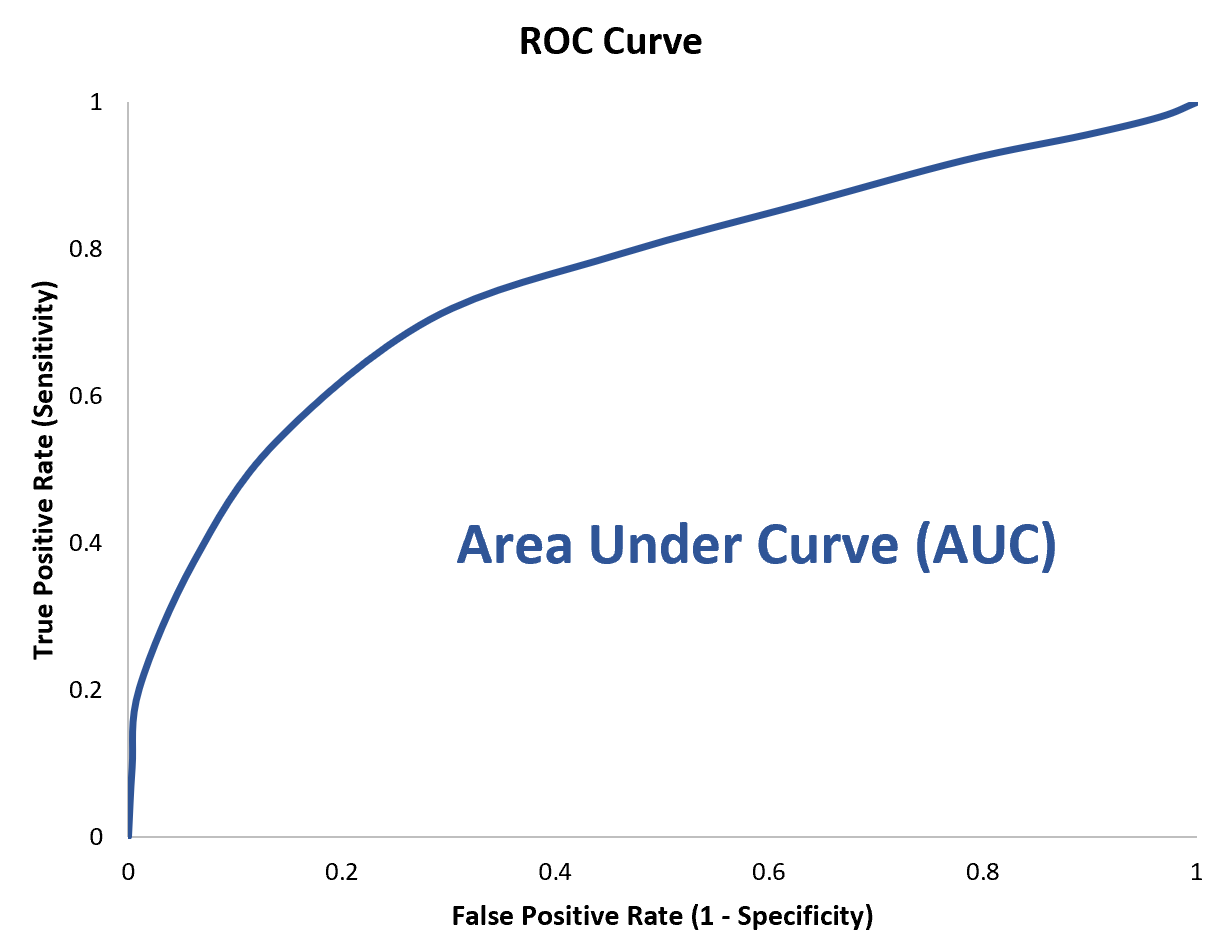
AUC が 1 に近づくほど、モデルは優れています。
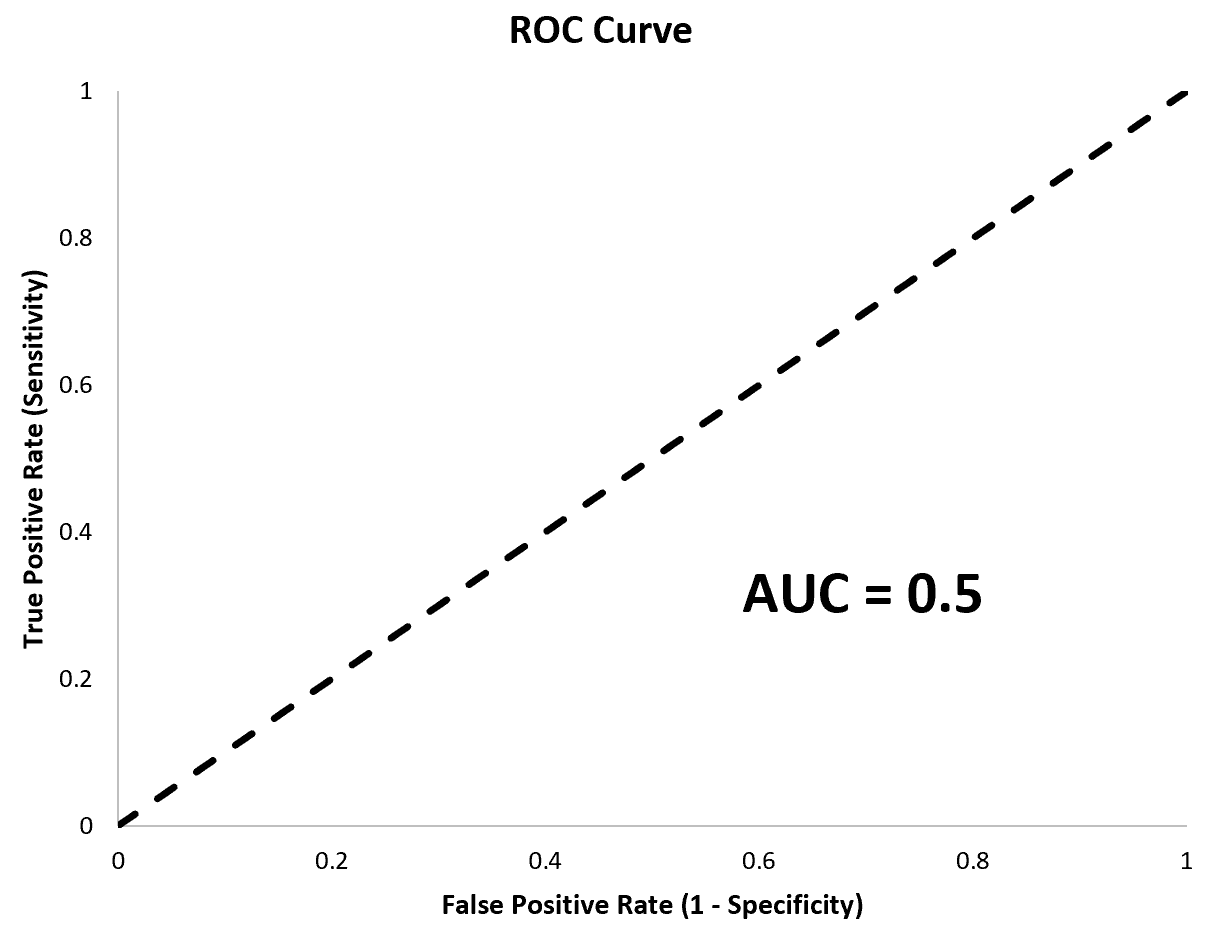
AUC が 0.5 に等しいモデルは完全な対角線となり、ランダムな分類を行うモデルと同等のモデルを表します。
複数のロジスティック回帰モデルの AUC を計算すると、どのモデルが予測に最も適しているかを確認できるため、特に便利です。
たとえば、3 つの異なるロジスティック回帰モデルを当てはめ、各モデルに対して次の ROC 曲線をプロットするとします。
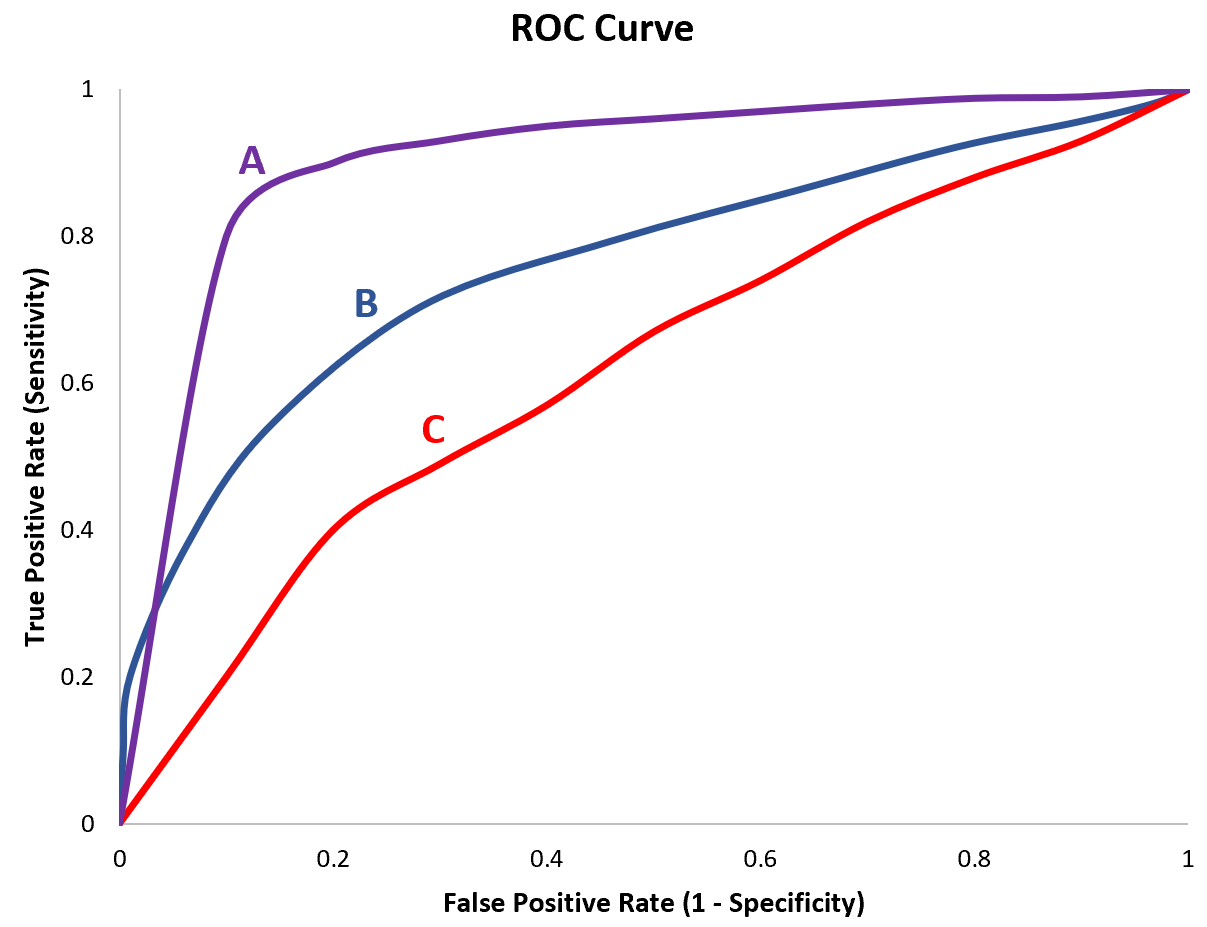
各モデルの AUC を次のように計算するとします。
- モデル A: AUC = 0.923
- モデル B: AUC = 0.794
- モデル C: AUC = 0.588
モデル A は最も高い AUC を持ち、これは曲線下面積が最も大きく、観測値をカテゴリーに正しく分類するのに最適なモデルであることを示しています。
追加リソース
次のチュートリアルでは、さまざまな統計ソフトウェアを使用して ROC 曲線を作成する方法を説明します。
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る