完全な多重共線性とは何ですか? (定義と例)
統計では、多重共線性は、2 つ以上の予測変数が相互に高度に相関しており、回帰モデル内で固有または独立した情報を提供しない場合に発生します。
変数間の相関度が十分に高い場合、回帰モデルのフィッティングと解釈の際に問題が発生する可能性があります。
多重共線性の最も極端なケースは、完全な多重共線性と呼ばれます。これは、2 つ以上の予測変数が互いに正確な線形関係を持つ場合に発生します。
たとえば、次のデータセットがあるとします。
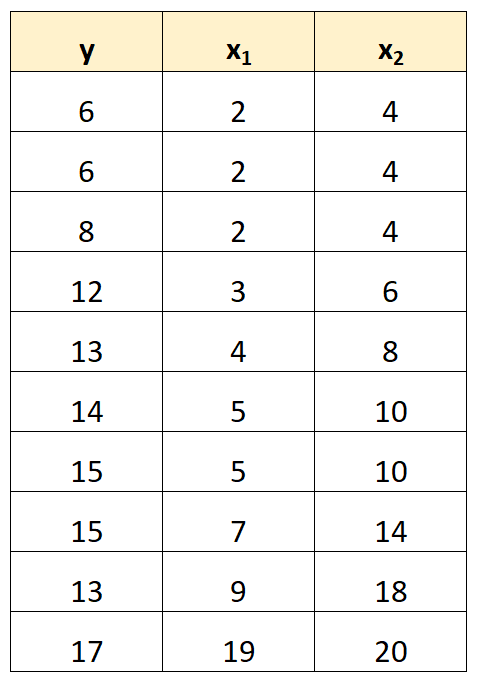
予測子変数 x 2の値は、単に x 1の値を 2 倍したものであることに注意してください。
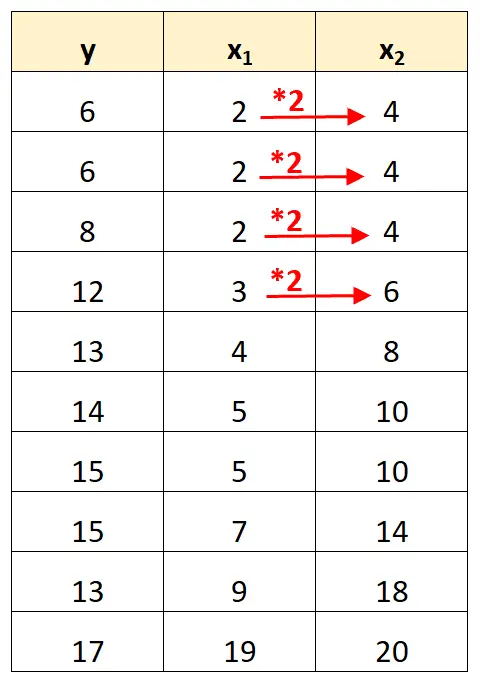
これは完全な多重共線性の例です。
完全多重共線性の問題
データセットに完全な多重共線性が存在する場合、通常の最小二乗法では回帰係数の推定値を生成できません。
実際、別の予測子変数 (x 2 ) を一定に保ちながら、応答変数 (y) に対する予測子変数 (x 1 ) の限界効果を推定することは不可能です。これは、x 1 が移動すると常に正確に x 2が移動するためです。
つまり、完全な多重共線性により、回帰モデルの各係数の値を推定することが不可能になります。
完全な多重共線性に対処する方法
完全な多重共線性を処理する最も簡単な方法は、別の変数と正確な線形関係がある変数の 1 つを削除することです。
たとえば、前のデータセットでは、単純に x 2 を予測子変数として削除できます。
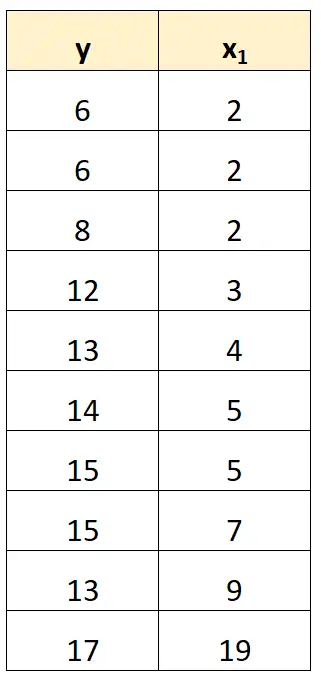
次に、x 1を予測変数として、y を応答変数として使用して回帰モデルを近似します。
完全な多重共線性の例
次の例は、実際に完全な多重共線性を示す 3 つの最も一般的なシナリオを示しています。
1. 予測変数は別の変数の倍数です
「身長(センチメートル)」と「身長(メートル)」を使用して、特定の種類のイルカの体重を予測したいとします。
データセットは次のようになります。
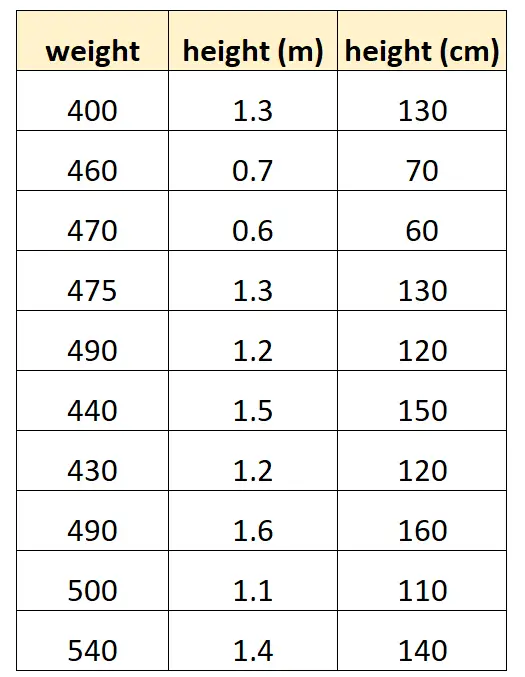
「センチメートル単位の高さ」の値は、単に「メートル単位の高さ」を 100 倍したものに等しいことに注意してください。これは、完全な多重共線性のケースです。
このデータセットを使用して R で重線形回帰モデルを近似しようとすると、予測変数「メートル」の係数推定値を生成できません。
#define data df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540), m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4), cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140)) #fit multiple linear regression model model <- lm(weight~m+cm, data=df) #view summary of model summary(model) Call: lm(formula = weight ~ m + cm, data = df) Residuals: Min 1Q Median 3Q Max -70,501 -25,501 5,183 19,499 68,590 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 458,676 53,403 8,589 2.61e-05 *** m 9.096 43.473 0.209 0.839 cm NA NA NA NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 41.9 on 8 degrees of freedom Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395
2. 予測変数は別の変数の変換バージョンです
「ポイント」と「スケール ポイント」を使用してバスケットボール選手の評価を予測したいとします。
変数「スケールされたポイント」が次のように計算されるとします。
スケールされたポイント = (ポイント – μポイント) / σポイント
データセットは次のようになります。
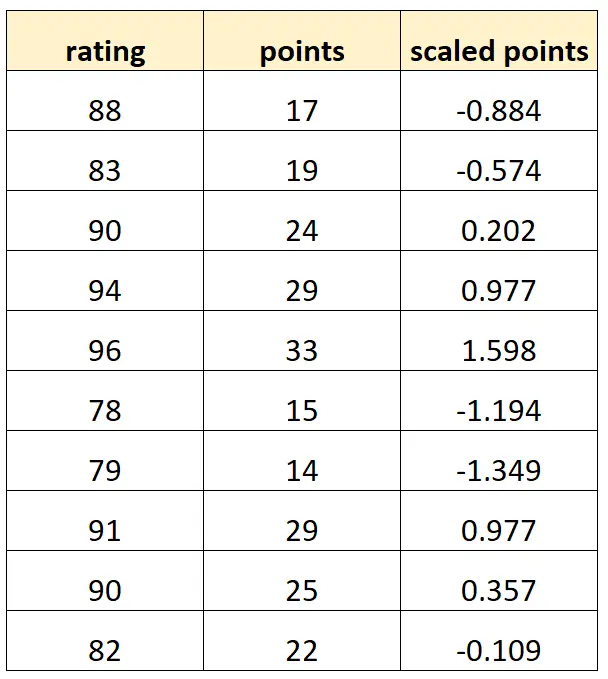
各「スケールされたポイント」の値は、単に「ポイント」の標準化されたバージョンであることに注意してください。これは完全な多重共線性のケースです。
このデータセットを使用して R で重線形回帰モデルを近似しようとすると、「スケーリングされたポイント」予測変数の係数推定値を生成できません。
#define data df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82), pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22)) df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts) #fit multiple linear regression model model <- lm(rating~pts+scaled_pts, data=df) #view summary of model summary(model) Call: lm(formula = rating ~ pts + scaled_pts, data = df) Residuals: Min 1Q Median 3Q Max -4.4932 -1.3941 -0.2935 1.3055 5.8412 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 67.4218 3.5896 18.783 6.67e-08 *** pts 0.8669 0.1527 5.678 0.000466 *** scaled_pts NA NA NA NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 2.953 on 8 degrees of freedom Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663
3. ダミー変数トラップ
完全な多重共線性が発生する可能性がある別のシナリオは、 ダミー変数トラップとして知られています。これは、回帰モデルでカテゴリ変数を取得し、それを 0、1、2 などの値を取る「ダミー変数」に変換したい場合です。
たとえば、予測変数「年齢」と「婚姻状況」を使用して収入を予測したいとします。

「婚姻状況」を予測変数として使用するには、まずそれをダミー変数に変換する必要があります。
これを行うには、これが最も頻繁に発生するため、「Single」を基本値として残し、次のように「Married」と「Divorce」に 0 または 1 の値を割り当てます。

間違いは、次のように 3 つの新しいダミー変数を作成することです。

この場合、「独身」変数は「既婚」変数と「離婚」変数の完全な線形結合です。これは完全な多重共線性の例です。
このデータセットを使用して R で重線形回帰モデルを近似しようとすると、各予測子変数の係数推定値を生成できなくなります。
#define data df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107), age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53), single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0), married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1), divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0)) #fit multiple linear regression model model <- lm(income~age+single+married+divorced, data=df) #view summary of model summary(model) Call: lm(formula = income ~ age + single + married + divorced, data = df) Residuals: Min 1Q Median 3Q Max -9.7075 -5.0338 0.0453 3.3904 12.2454 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 16.7559 17.7811 0.942 0.37739 age 1.4717 0.3544 4.152 0.00428 ** single -2.4797 9.4313 -0.263 0.80018 married NA NA NA NA divorced -8.3974 12.7714 -0.658 0.53187 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 8.391 on 7 degrees of freedom Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865
追加リソース
回帰における多重共線性と VIF のガイド
RでVIFを計算する方法
Python で VIF を計算する方法
ExcelでVIFを計算する方法