相対リスクの信頼区間を計算する方法

相対リスクは、次の形式の 2×2 テーブルを分析するときに計算されることがよくあります。

相対リスクは、対照グループで発生するイベントの可能性と比較した、治療グループでイベントが発生する可能性を示します。

次のように計算されます。

• 相対リスク= [A/(A+B)] / [C/(C+D)]

次に、次の式を使用して、相対リスク (RR) の信頼区間を計算できます。

• 95% 未満の CI = e ^{ln(RR) – 1.96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}
• 95% を超える CI = e ^{ln(RR) + 1.96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}

次の例は、実際に相対リスクと対応する信頼区間を計算する方法を示しています。

例: 相対リスクの信頼区間の計算

バスケットボールのコーチが新しいトレーニング プログラムを使用して、古いトレーニング プログラムと比較して、特定のスキル テストに合格できる選手の数が増加するかどうかを確認するとします。

コーチは各プログラムを使用する 50 人の選手を募集します。次の表は、使用したプログラムに基づいて、スキル テストに合格したプレーヤーと不合格になったプレーヤーの数を示しています。

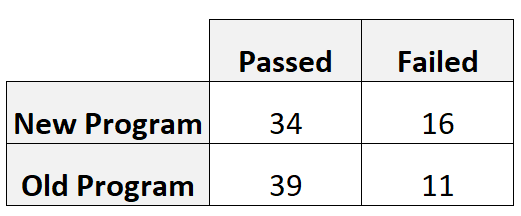
相対リスクは次のように計算できます。

• 相対リスク = [A/(A+B)] / [C/(C+D)]
• 相対リスク = [34/(34+16)] / [39/(39+11)]
• 相対リスク = 0.8718

これは、新しいプログラムを使用してプレーヤーがテストに合格する確率は、古いプログラムを使用してプレーヤーがテストに合格する確率の 0.8718 倍しかないことを意味すると解釈します。

言い換えれば、新しいプログラムの使用により、プレーヤーがテストに合格する可能性は実際には減少します。

次に、次の式を使用して、相対リスクの 95% 信頼区間を計算できます。

• 95% 未満の CI = e ^{ln(.8718) – 1.96√ (1/34 + 1/39 – 1/(34+16) – 1/(39+11)} = 0.686
• 95% を超える CI = e ^{ln(.8718) + 1.96√ (1/34 + 1/39 + 1/(34+16) – 1/(39+11)} = 1.109

したがって、相対リスクの 95% 信頼区間は[0.686, 1.109]です。

新しいトレーニング プログラムと古いトレーニング プログラムの間の真の相対リスクがこの間隔内に収まることを 95% 確信しています。

この信頼区間には値 1 が含まれているため、統計的に有意ではありません。

これは、次の点を考慮すると理解できるはずです。

• 相対リスクが 1 より大きい場合は、新しいプログラムを使用してプレーヤーがテストに合格する確率が、古いプログラムを使用してプレーヤーがテストに合格する確率よりも高いことを意味します。
• 1 未満の相対リスクは、新しいプログラムを使用してプレーヤーがテストに合格する確率が、古いプログラムを使用してプレーヤーがテストに合格する確率よりも低いことを意味します。

したがって、相対リスクの 95% 信頼区間には値 1 が含まれているため、これは、プレーヤーが新しいプログラムを使用してスキル テストに合格する確率は、同じプレーヤーが新しいプログラムを使用してテストに合格する確率よりも大きい場合もあれば、そうでないこともあるということを意味します。新しいプログラム。古いプログラム。

追加リソース

次のチュートリアルでは、オッズ比と相対リスクに関する追加情報を提供します。

オッズ比の解釈方法
相対リスクをどう解釈するか
Excel でオッズ比と相対リスクを計算する方法