回帰勾配の標準誤差を理解する
回帰勾配の標準誤差は、回帰勾配を推定する際の「不確実性」を測定する方法です。
次のように計算されます。
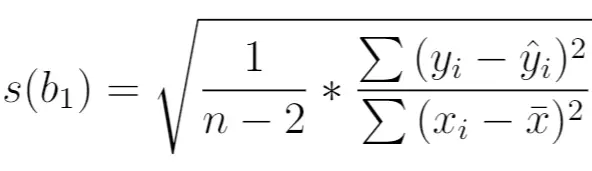
金:
- n : 合計サンプルサイズ
- y i : 応答変数の実数値
- ŷ i : 応答変数の予測値
- x i : 予測変数の実数値
- x̄ : 予測変数の平均値
標準誤差が小さいほど、回帰勾配の係数推定値のばらつきが小さくなります。
回帰勾配の標準誤差は、ほとんどの統計ソフトウェアの回帰出力の「標準誤差」列に表示されます。
次の例は、2 つの異なるシナリオで回帰勾配の標準誤差を解釈する方法を示しています。
例 1: 回帰勾配の小さな標準誤差の解釈
教授が、クラスの生徒の勉強時間数と最終試験の成績との関係を理解したいとします。
25 人の生徒のデータを収集し、次の散布図を作成します。
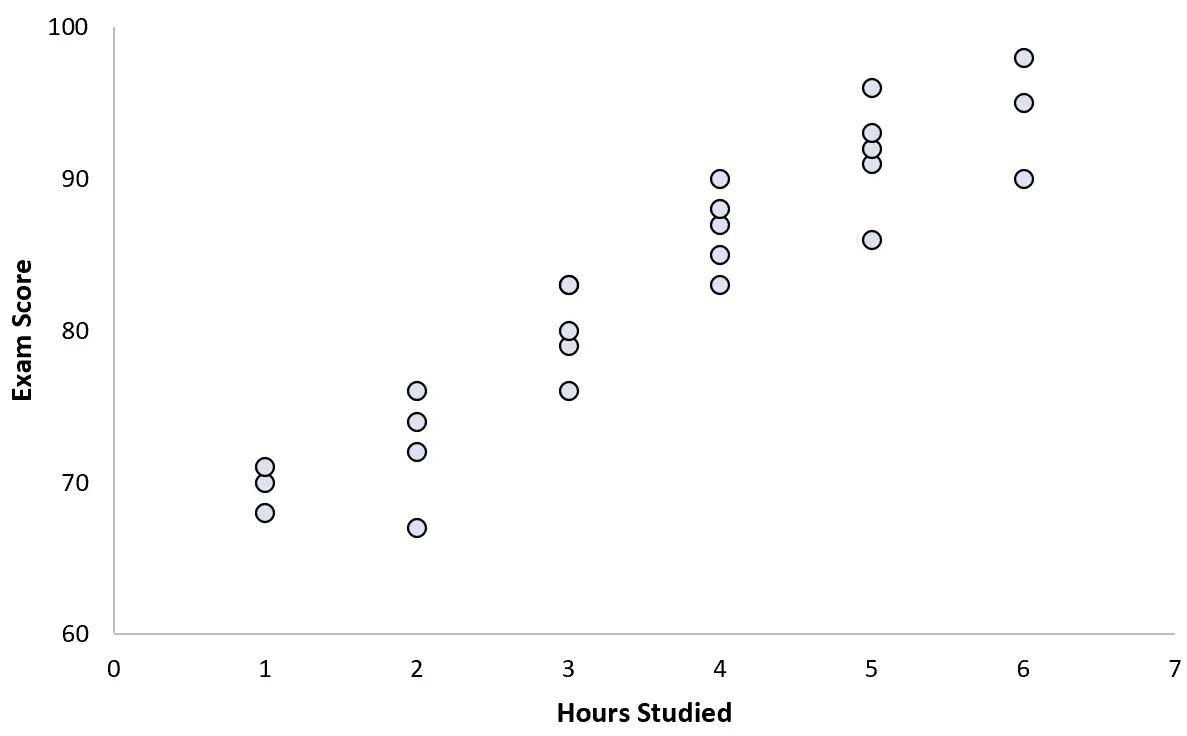
2 つの変数の間には明らかに正の相関関係があります。学習時間数が増加すると、試験のスコアはかなり予測可能な割合で増加します。
次に、学習時間を予測変数として、最終試験の成績を応答変数として使用して、単純な線形回帰モデルを当てはめました。
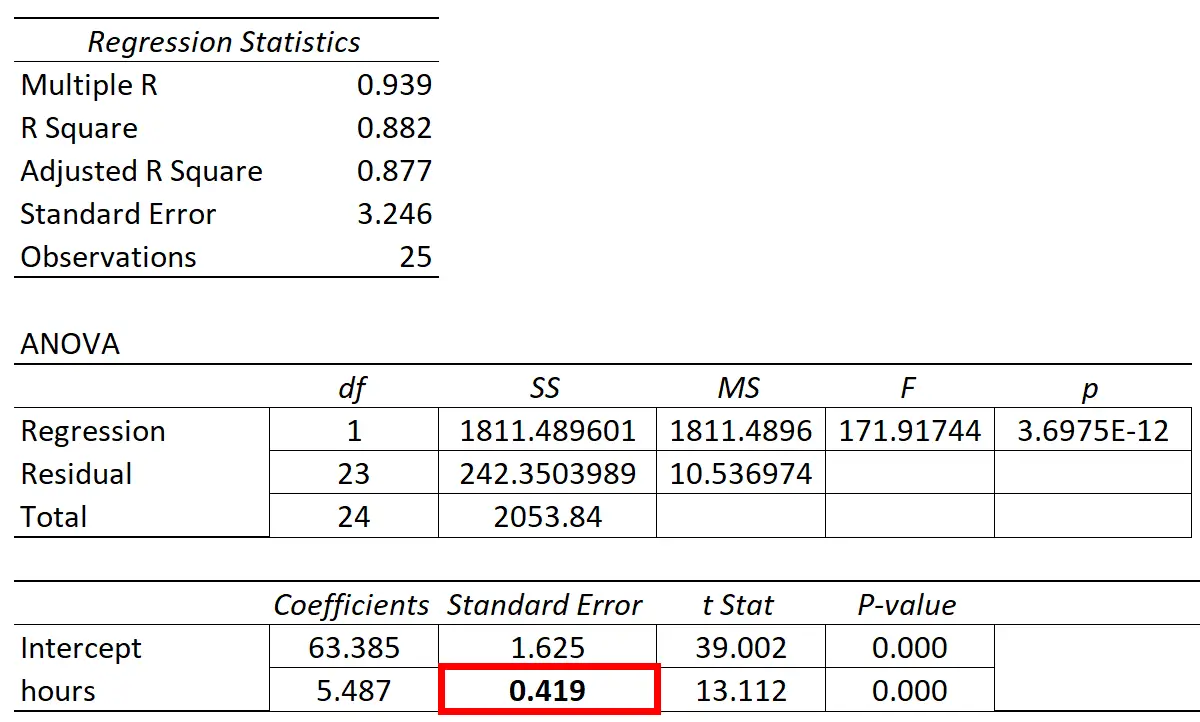
次の表に回帰結果を示します。
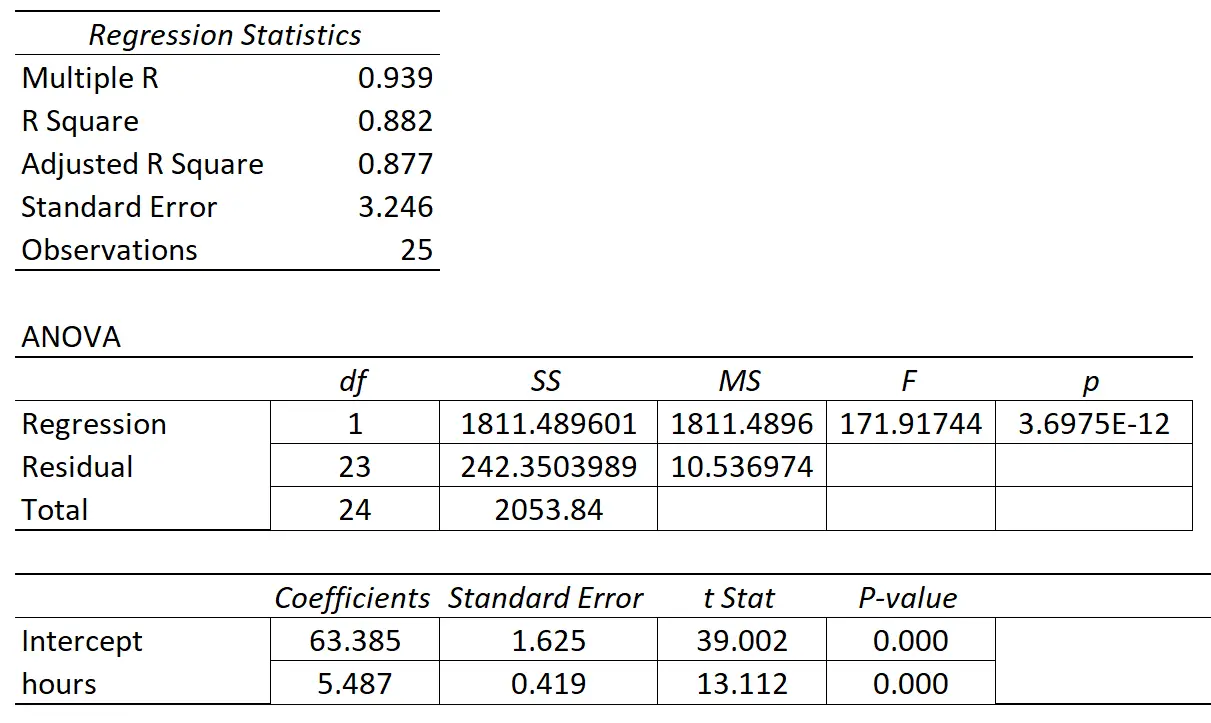
予測変数「学習時間」の係数は 5.487 です。これは、学習時間が 1 時間増えるごとに、試験のスコアが平均5,487上昇することを示しています。
標準誤差は0.419で、回帰勾配のこの推定値付近のばらつきの尺度を表します。
この値を使用して、予測変数「学習時間」の t 統計を計算できます。
- t 統計量 = 係数推定値 / 標準誤差
- t 統計量 = 5.487 / 0.419
- t 統計量 = 13.112
このテスト統計に対応する p 値は 0.000 で、これは「学習時間」が最終試験の成績と統計的に有意な関係があることを示しています。
回帰勾配の標準誤差は回帰勾配の係数推定値と比較して小さいため、予測変数は統計的に有意でした。
例 2: 回帰勾配の大きな標準誤差の解釈
別の教授が、クラスの学生の学習時間数と最終試験の成績との関係を理解したいとします。
彼女は 25 人の生徒のデータを収集し、次の散布図を作成しました。
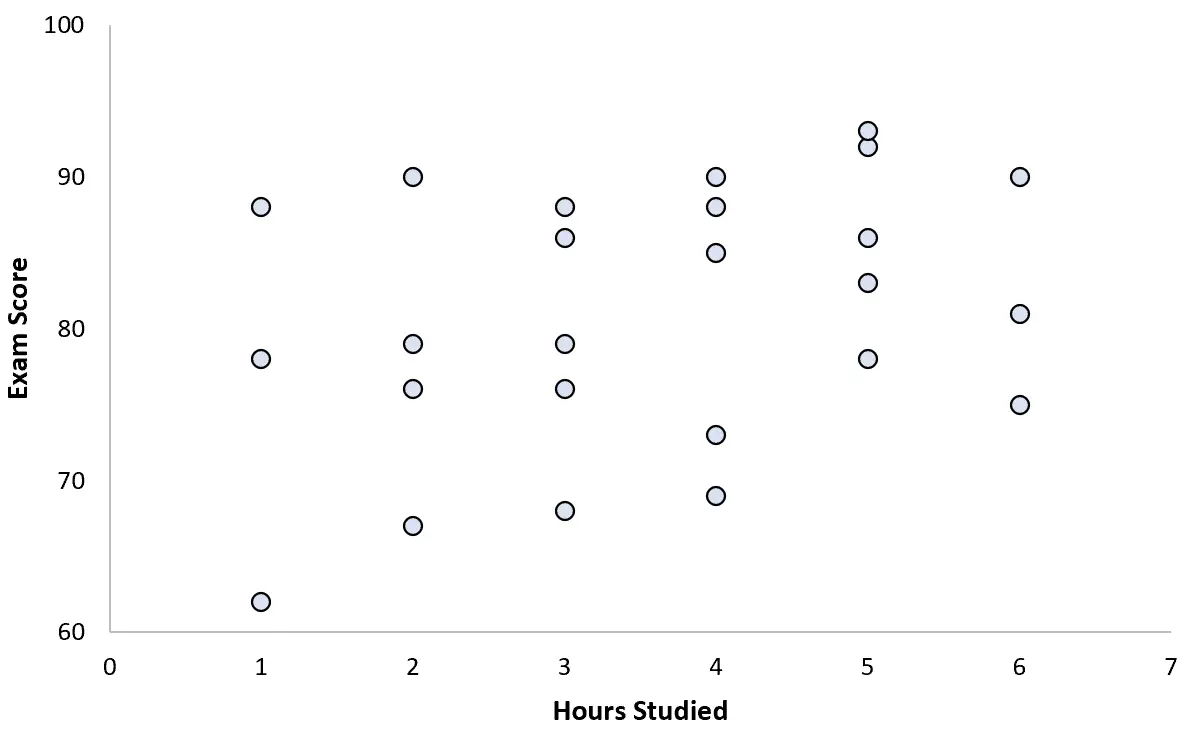
2 つの変数の間にはわずかな正の相関があるようです。学習時間の増加に伴い、試験のスコアは一般的に増加しますが、その割合は予測可能なものではありません。
次に、教授が学習時間を予測変数として、最終試験の成績を応答変数として使用して、単純な線形回帰モデルを当てはめたと仮定します。
次の表に回帰結果を示します。
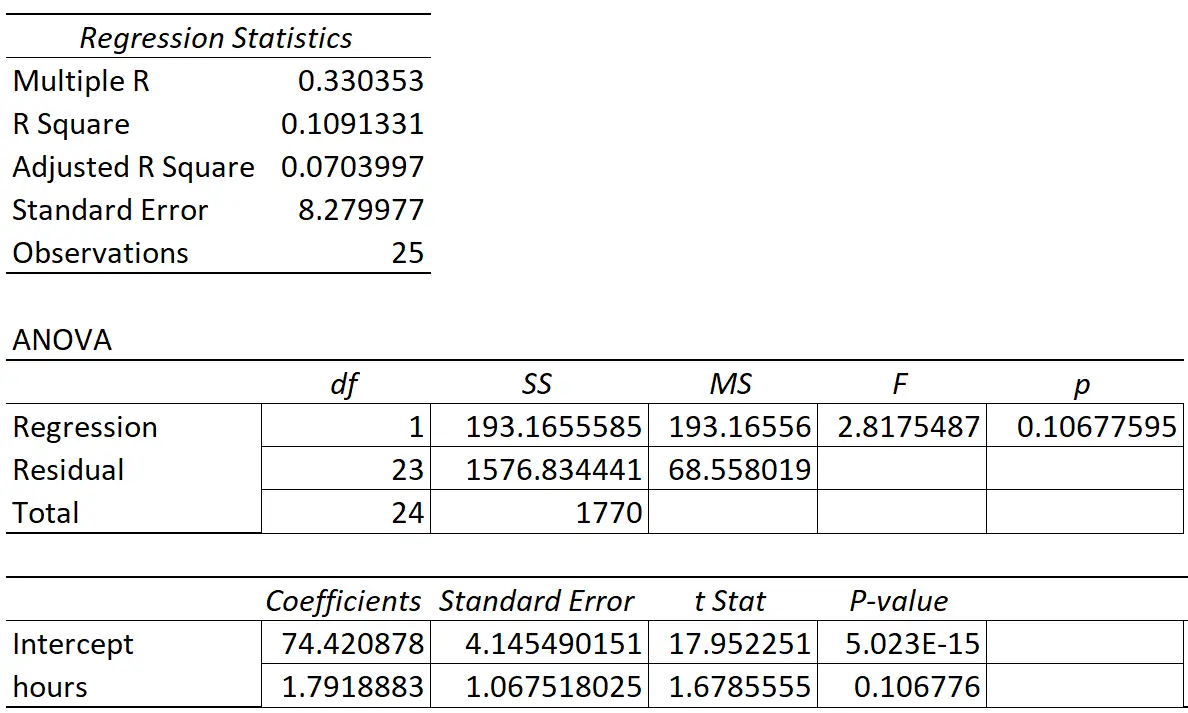
予測変数「学習時間」の係数は 1.7919 です。これは、学習時間が追加されるごとに、試験のスコアが平均1.7919増加することを示しています。
標準誤差は1.0675で、これは回帰勾配のこの推定値付近のばらつきの尺度です。
この値を使用して、予測変数「学習時間」の t 統計を計算できます。
- t 統計量 = 係数推定値 / 標準誤差
- t 統計量 = 1.7919 / 1.0675
- t 統計量 = 1.678
この検定統計量に対応する p 値は 0.107 です。この p 値は 0.05 未満ではないため、「学習時間」と最終試験の成績には統計的に有意な関係がないことがわかります。
回帰勾配の標準誤差が回帰勾配の係数推定値に比べて大きかったため、予測変数は統計的に有意ではありませんでした。