ベンフォードの法則
この記事ではベンフォードの法則とは何かについて説明します。さらに、ベンフォードの法則がどのように発見されたのか、そしてこの統計法則がどのように応用されるのかを知ることができます。
ベンフォードの法則とは何ですか?
ベンフォードの法則 は、 「最初の桁の法則」とも呼ばれ、データの最初の桁が 1 である確率は、別の数値である確率よりも大きいという統計法則です。
つまり、ベンフォードの法則は、現実に存在する一連の数値データにおいて、数字 1 がデータの最初の桁として最も多く繰り返される数字である、というものです。
さらに、数値が高くなるほど、1 位になる可能性は低くなります。したがって、最初の数字は 2 よりも 1 である可能性が高くなりますが、3 よりも 2 の可能性が高く、4 よりも 3 の可能性が高くなります。
ベンフォードの法則の名前は、アメリカ人のフランク・ベンフォードに由来します。ベンフォードが発明したわけではありませんが、この統計法則を広めたのがベンフォードです。以下ではベンフォードの法則の起源を見ていきます。
ベンフォードの法則の公式
ベンフォードの法則では、最初の桁が特定の数値である確率は、その数値に 1 を加えた対数に等しいと定められています。
したがって、ベンフォードの法則の公式は次のようになります。
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a77defb5b209293a074ac2bee02c2e07_l3.png)
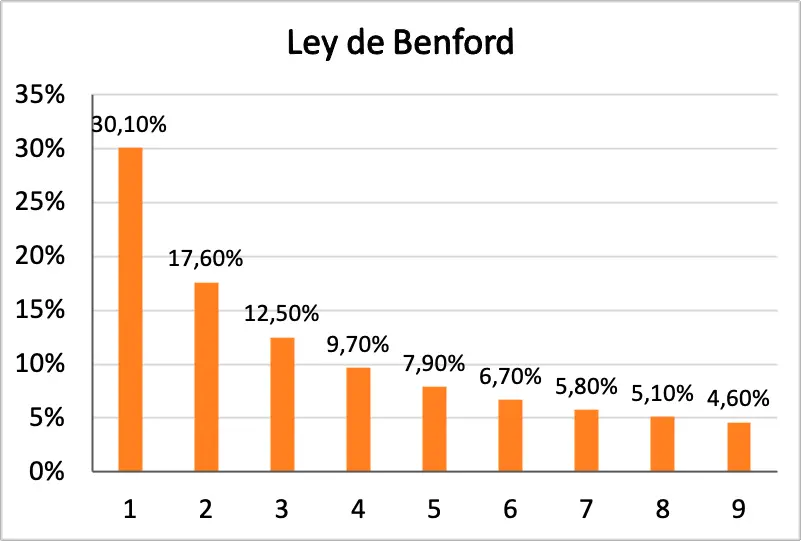
したがって、ベンフォードの法則の公式から、各数値がデータ項目の最初の桁である確率を導き出すことができます。次の表では、すべての確率のパーセンテージを確認できます。
| 形 | その確率 最初の番号になる |
|---|---|
| 1 | 30.1% |
| 2 | 17.6% |
| 3 | 12.5% |
| 4 | 9.7% |
| 5 | 7.9% |
| 6 | 6.7% |
| 7 | 5.8% |
| 8 | 5.1% |
| 9 | 4.6% |
さらに、ベンフォードの法則のすべての確率がグラフで表されたヒストグラムを以下に示します。
ベンフォードの法則の歴史
1881 年、数学者サイモン ニューカムは、対数表の最初のページが最後のページよりもかなり多く使用されていることを発見し、ベンフォードの法則を推定しました。つまり、数字の最初の桁の可能性は同じではありませんが、1 は 2 よりも頻繁に、2 は 3 よりも多く、同様に 9 まで続くことになります。
しかし、ニューカムはこの規則が守られたという統計的証拠を何も残さず、単に対数表の磨耗から推論しただけでした。
その後、具体的には 1938 年に、物理学者のフランク ベンフォードも同じ観察を行い、それを経験的に検証するための実験も行いました。彼は、20 の異なるサンプルからの 20,229 個の値の統計データ セットについて、各データの最初の桁について調査を実行しました。そこで、その結果に基づいて、彼はベンフォードの法則が成り立つことを実証し、最初の桁が特定の数値である確率を計算できる公式を導き出しました (この公式は上で見ました)。
つまり、ベンフォードの法則はサイモン・ニューカムによって最初に発見されましたが、彼がこの統計法則を検証した人であるため、フランク・ベンフォードにちなんで名付けられました。
ベンフォードの法則の応用
ベンフォードの法則は、さまざまな分野に応用できる統計法則です。たとえば、ベンフォードの法則は、経済学、生物学、さらには政治の分野でも広く使用されています。
経済学では、データセットがベンフォードの法則に適合しない場合、データが操作されたことを示すため、ベンフォードの法則はデータ操作の検出によく使用されます。この法律は、たとえば、税金詐欺の可能性のあるケースを検出するために使用されます。
ベンフォードの法則は、結果が確率的に等しいため、ランダム現象の真実性を証明するためには使用されないことに注意してください。したがって、ベンフォードの法則を宝くじ結果の検証に使用することはできません。
一方、遺伝学では、ベンフォードの法則を使用して、異なる種類の生物間のゲノム長の違いを分析できます。
最後に、ベンフォードの法則を適用して不正投票を検出する試みも行われていますが、この場合の有用性は疑問視されています。