重回帰の 5 つの仮定
重線形回帰は、複数の予測変数と応答変数の間の関係を理解するために使用できる統計手法です。
ただし、多重線形回帰を実行する前に、まず次の 5 つの前提が満たされていることを確認する必要があります。
1. 線形関係:各予測変数と応答変数の間には線形関係があります。
2. 多重共線性なし:どの予測変数も相互に高度に相関しません。
3. 独立性:観察は独立しています。
4. 等分散性:線形モデルの各点で残差は一定の分散を持ちます。
5. 多変量正規性:モデルの残差は正規分布します。
これらの仮定の 1 つ以上が満たされない場合、重回帰の結果は信頼できない可能性があります。
この記事では、各前提の説明、前提が満たされているかどうかを判断する方法、前提が満たされていない場合の対処方法について説明します。
仮説 1: 線形関係
重線形回帰では、各予測変数と応答変数の間に線形関係があると仮定します。
この仮定が満たされているかどうかを判断する方法
この仮定が満たされているかどうかを判断する最も簡単な方法は、各予測変数と応答変数の散布図を作成することです。
これにより、2 つの変数間に線形関係があるかどうかを視覚的に確認できます。
散布図内の点がほぼ直線の対角線に沿って配置されている場合、変数間に線形関係がある可能性があります。
たとえば、以下のグラフ内の点は直線上にあるように見えます。これは、この特定の予測変数 (x) と応答変数 (y) の間に線形関係があることを示しています。

この前提が尊重されない場合はどうすればよいか
1 つ以上の予測変数と応答変数の間に線形関係がない場合、いくつかのオプションがあります。
1.予測子変数に非線形変換を適用します (対数や平方根など)。これにより、関係がより直線的なものになることがよくあります。
2.別の予測子変数をモデルに追加します。たとえば、x と y のプロットが放物線状の場合、モデルに追加の予測子変数として X 2を追加することが合理的である可能性があります。
3.モデルから予測変数を削除します。最も極端なケースでは、特定の予測変数と応答変数の間に線形関係がない場合、その予測変数をモデルに含めることは役に立たない可能性があります。
仮説 2: 多重共線性はない
多重線形回帰では、どの予測変数も相互に高度な相関がないことを前提としています。
1 つ以上の予測子変数の相関性が高い場合、回帰モデルは多重共線性の影響を受け、モデルの係数推定の信頼性が低くなります。
この仮定が満たされているかどうかを判断する方法
この仮定が満たされているかどうかを判断する最も簡単な方法は、各予測子変数の VIF 値を計算することです。
VIF 値は 1 から始まり、上限はありません。一般に、5* を超える VIF 値は、潜在的な多重共線性を示します。
次のチュートリアルでは、さまざまな統計ソフトウェアで VIF を計算する方法を示します。
*研究分野によっては、研究者が代わりに VIF 値 10 を使用する場合があります。
この前提が尊重されない場合はどうすればよいか
1 つ以上の予測子変数の VIF 値が 5 より大きい場合、この問題を解決する最も簡単な方法は、高い VIF 値を持つ予測子変数を単純に削除することです。
あるいは、各予測子変数をモデル内に保持したい場合は、相関性の高い予測子変数を処理するように設計された、リッジ回帰、ラッソ回帰、部分最小二乗回帰などの別の統計手法を使用できます。
仮説 3: 独立性
重回帰では、データセット内の各観測値が独立していると仮定します。
この仮定が満たされているかどうかを判断する方法
この仮定が満たされているかどうかを判断する最も簡単な方法は、 ダービン・ワトソン検定を実行することです。これは、残差 (したがって観測値) が自己相関を示すかどうかを示す正式な統計検定です。
この前提が尊重されない場合はどうすればよいか
この前提にどのように違反するかに応じて、いくつかの選択肢があります。
- 正の系列相関を得るには、従属変数および/または独立変数のラグをモデルに追加することを検討してください。
- 負のシリアル相関の場合は、どの変数も遅延しすぎていないことを確認してください。
- 季節相関については、モデルに季節ダミーを追加することを検討してください。
仮説 4: 等分散性
多重線形回帰では、線形モデルの各点で残差の分散が一定であると仮定します。そうでない場合、残差は不均一分散性の影響を受けます。
回帰分析に不均一分散性が存在する場合、回帰モデルの結果は信頼性が低くなります。
具体的には、不均一分散性により回帰係数推定値の分散が増加しますが、回帰モデルではそれが考慮されていません。これにより、実際にはそうではないにもかかわらず、回帰モデルがモデル内の項が統計的に有意であると主張する可能性が非常に高くなります。
この仮定が満たされているかどうかを判断する方法
この仮定が満たされているかどうかを判断する最も簡単な方法は、予測値に対する標準化残差のプロットを作成することです。
回帰モデルをデータセットに適合させたら、応答変数の予測値を X 軸に、モデルの標準化された残差を X 軸に表示する散布図を作成できます。やあ。
散布図内の点が傾向を示している場合、不均一分散が存在します。
次のグラフは、不均一分散性が問題にならない回帰モデルの例を示しています。
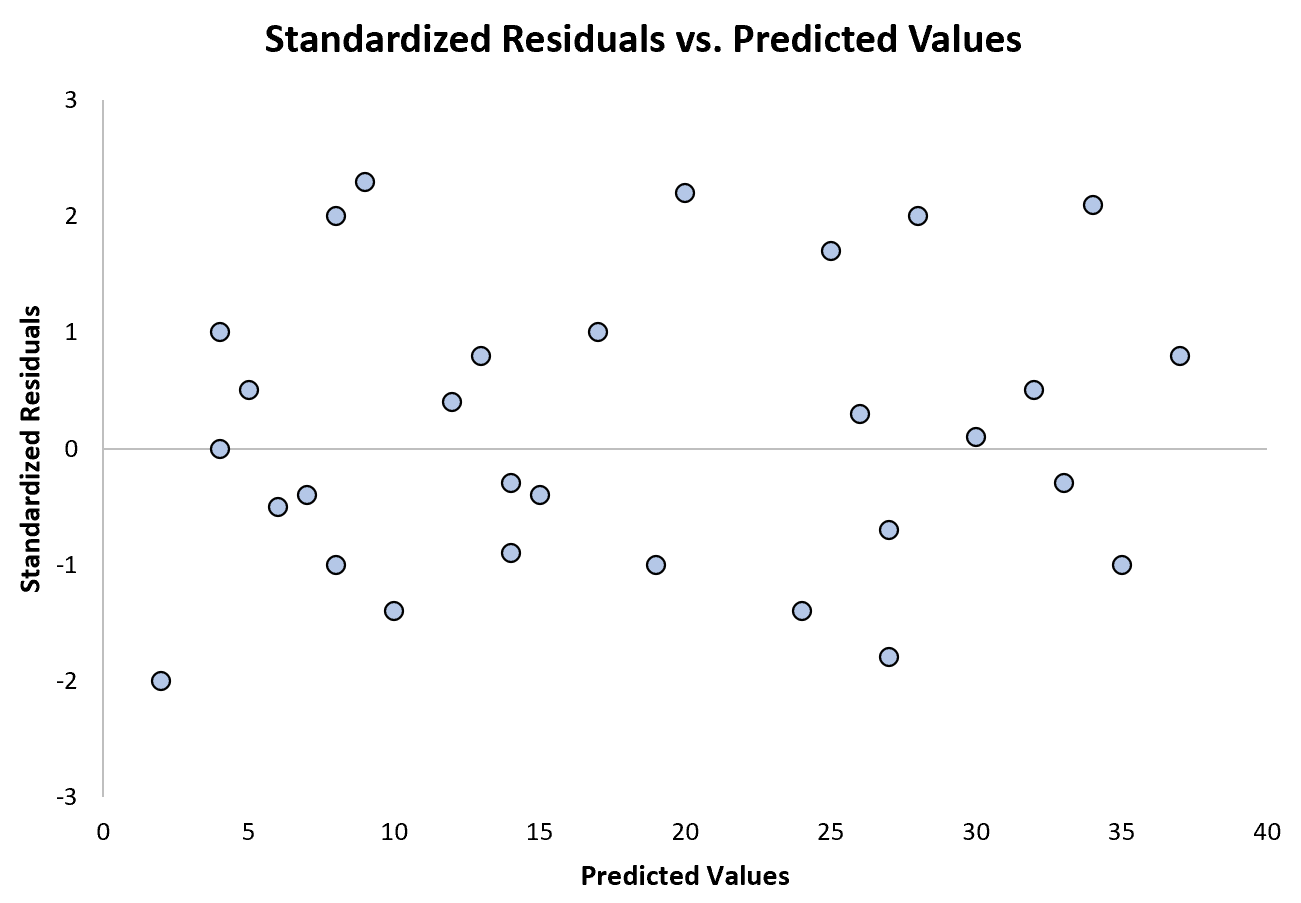
標準化された残差は明確なパターンがなくゼロの周囲に散在していることに注意してください。
次のグラフは、不均一分散性が問題となる回帰モデルの例を示しています。
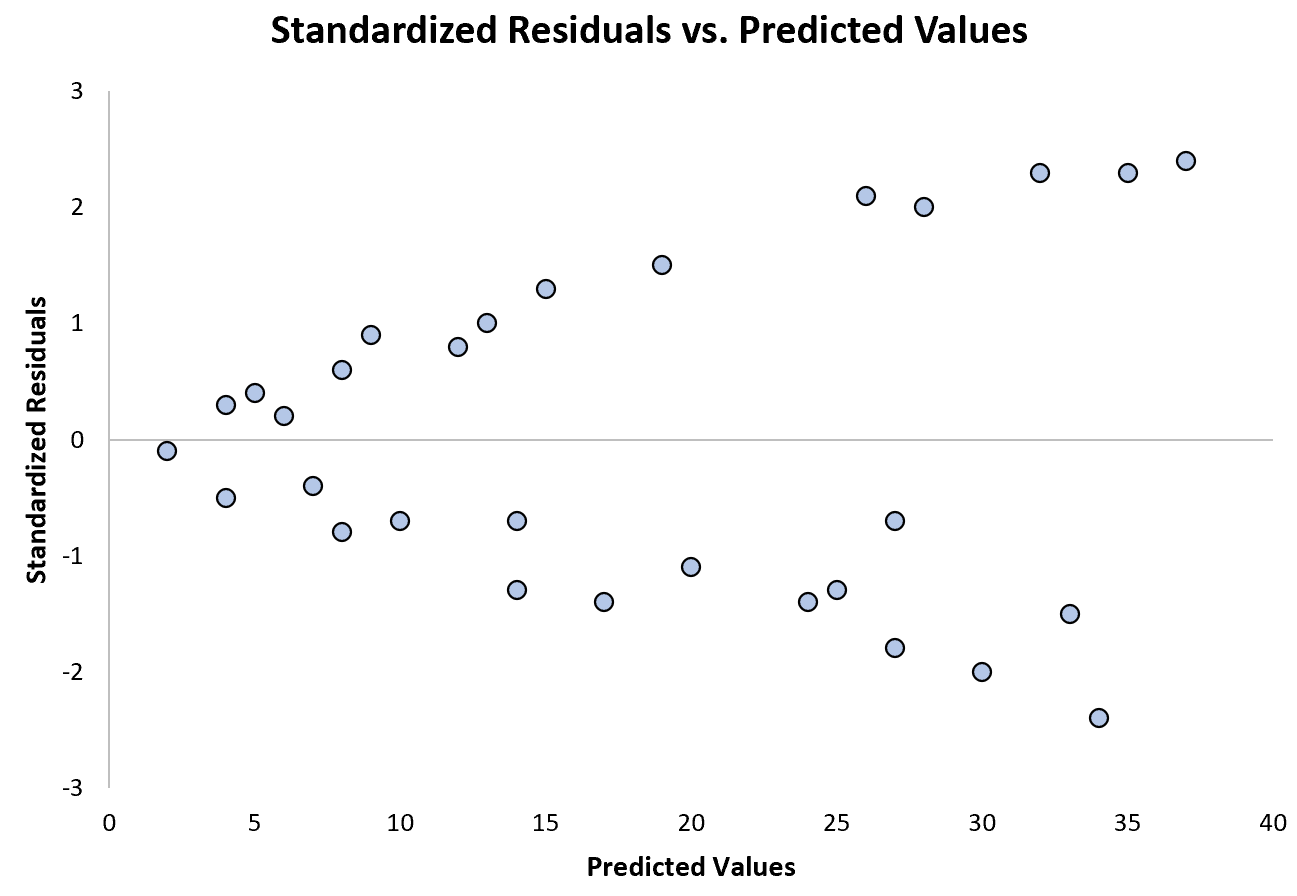
予測値が増加するにつれて、標準化された残差がどのように広がるかに注目してください。この「円錐」の形状は、不均一分散性の典型的な兆候です。
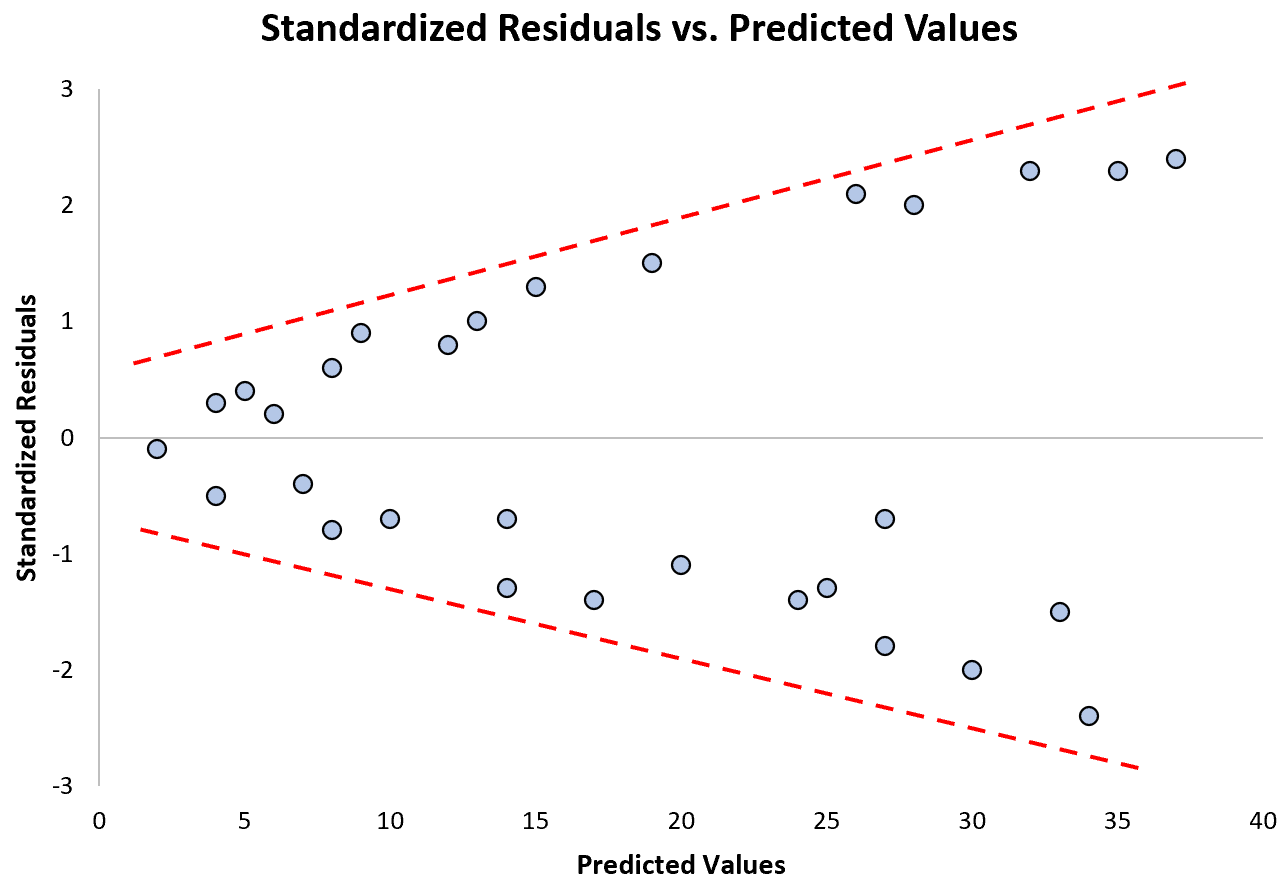
この前提が尊重されない場合はどうすればよいか
不均一分散性を補正するには、次の 3 つの一般的な方法があります。
1. 応答変数を変換します。不均一分散性に対処する最も一般的な方法は、応答変数のすべての値の対数、平方根、または立方根を取得して応答変数を変換することです。これにより、不均一分散性が消失することがよくあります。
2. 応答変数を再定義します。応答変数を再定義する 1 つの方法は、生の値ではなく率を使用することです。たとえば、人口規模を使用して都市の花屋の数を予測する代わりに、人口規模を使用して 1 人あたりの花屋の数を予測できます。
ほとんどの場合、花屋の数自体ではなく、一人あたりの花屋の数を測定しているため、これにより、より大きな集団内で自然に発生する変動が軽減されます。
3. 重み付け回帰を使用します。不均一分散性を補正するもう 1 つの方法は、重み付き回帰を使用することです。これは、近似値の分散に基づいて各データ ポイントに重みを割り当てます。
基本的に、これにより、分散が大きいデータ ポイントに低い重みが与えられ、残差二乗が減少します。適切な重みを使用すると、不均一分散性の問題を解決できます。
関連: R で加重回帰を実行する方法
仮定 4: 多変量正規性
重線形回帰では、モデルの残差が正規分布していると仮定します。
この仮定が満たされているかどうかを判断する方法
この仮定が満たされているかどうかを確認するには、次の 2 つの一般的な方法があります。
1. QQ プロットを使用して仮説を視覚的に検証します。
QQ プロット (分位数-分位数プロットの略) は、モデルの残差が正規分布に従うかどうかを判断するために使用できるプロットの一種です。プロット上の点がほぼ直線の対角線を形成している場合は、正規性の仮定が満たされています。
次の QQ プロットは、正規分布にほぼ従う残差の例を示しています。
ただし、以下の QQ プロットは、残差が直線の対角線から明らかに逸脱しており、正規分布に従っていないことを示している場合の例を示しています。
2. Shapiro-Wilk、Kolmogorov-Smironov、Jarque-Barre、D’Agostino-Pearson などの正式な統計検定を使用して仮説を検証します。
これらのテストはサンプル サイズが大きい場合に敏感であることに注意してください。つまり、サンプル サイズが非常に大きい場合、残差は正規ではないと結論付けることがよくあります。この仮説を検証するには、QQ プロットなどのグラフィカルな手法を使用する方が簡単な場合が多いのはこのためです。
この前提が尊重されない場合はどうすればよいか
正規性の仮定が満たされない場合、いくつかの選択肢があります。
1.まず、正規性の仮定に違反するような極端な外れ値がデータ内に存在しないことを確認します。
2.次に、応答変数のすべての値の平方根、対数、または立方根を取得するなどして、応答変数に非線形変換を適用できます。これにより、多くの場合、モデル残差がより正規分布になります。
追加リソース
次のチュートリアルでは、重線形回帰とその仮定に関する追加情報を提供します。
重線形回帰の概要
回帰分析における不均一分散性のガイド
回帰における多重共線性と VIF のガイド
次のチュートリアルでは、さまざまな統計ソフトウェアを使用して重線形回帰を実行する方法について、段階的な例を示します。
Excelで重回帰を実行する方法
R で重回帰を実行する方法
SPSS で重回帰を実行する方法
Stata で重回帰を実行する方法