経済学における統計の重要性 (例付き)

統計の分野は、データの収集、分析、解釈、表示に関係します。

経済学の分野では、次の理由から統計が重要です。

理由 1 : 統計は、経済学者が記述統計を使用して経済の状態を理解することを可能にします。

理由 2 : 統計により、経済学者はデータの視覚化を使用して経済の傾向を見つけることができます。

理由 3 : 統計により、経済学者は回帰モデルを使用して変数間の関係を定量化できます。

理由 4 : 統計により、経済学者は経済の傾向を予測できます。

この記事の残りの部分では、これらのそれぞれの理由を説明します。

理由 1: 記述統計を使用して経済学を理解する

記述統計はデータを説明するために使用されます。

経済学者は、特定の地域について次の記述統計を計算することがよくあります。

• 平均世帯収入。
• 世帯収入の標準偏差。
• 国内総生産の合計。
• 新規雇用の合計における割合の変化。

これらの測定を通じて、経済学者は特定の地域の経済の状態をより深く理解できるようになります。

次に、これらの測定値を使用して、経済の健全性と成長を維持するために使用する最適な方法を政治家や議員に知らせることができます。

注: これらのタイプの記述統計は、経済のあらゆるレベルで使用されます。たとえば、国レベル、州レベル、都市レベル、郡レベルなどの経済学者です。全員が、地域の経済状態をより深く理解するために記述統計を使用しています。

理由 2: データの視覚化を使用して傾向を特定する

経済学で統計を使用するもう 1 つの一般的な方法は、折れ線グラフ、ヒストグラム、箱ひげ図、円グラフ、その他のグラフなどのデータを視覚化することです。

これらのタイプのグラフは、経済学者が経済が改善しているか悪化しているかを判断するのに役立つ傾向を特定するのによく使用されます。

たとえば、経済学者が、特定の都市の全体的な失業率を年ごとに示す次の折れ線グラフを作成したとします。

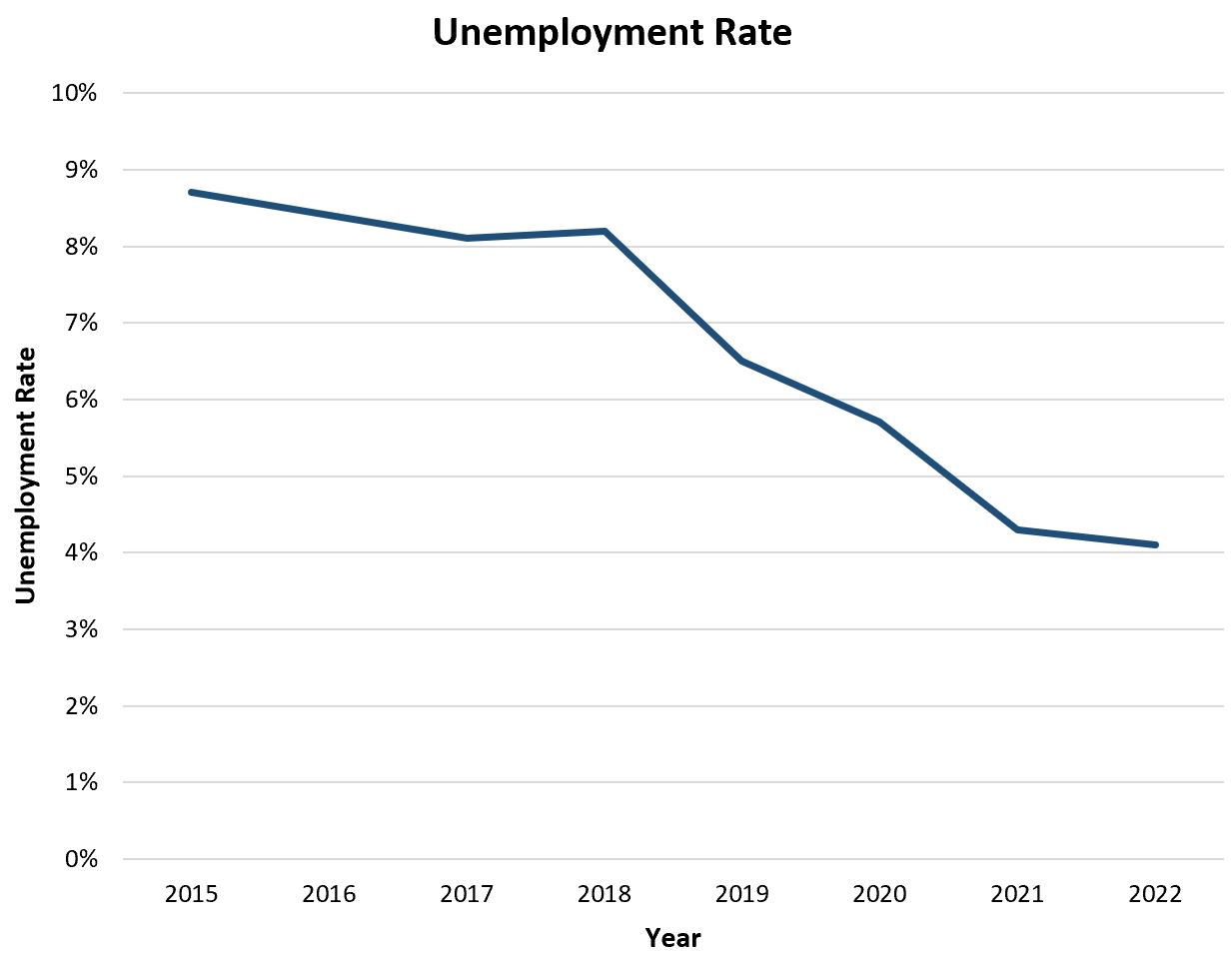
経済学者はこの棒グラフを見るだけで、失業率が時間の経過とともに減少していることがわかります。これは、経済が好調で、仕事を見つける国民が増えていることを示しています。

理由 3: 回帰モデルを使用して変数間の関係を定量化する

統計は経済学でも回帰モデルの形で使用されます。

これらは、経済学者が 1 つ以上の予測変数と応答変数の間の関係を定量化できるようにするモデルです。

たとえば、経済学者は、特定の都市の総教育年数、週の労働時間、世帯収入に関するデータにアクセスできるとします。

次に、次の重線形回帰モデルを構築できます。

収入 = 35,870.22 + 1,500.24 (教育年数) + 400.34 (週あたりの労働時間)

このモデルの回帰係数を解釈する方法は次のとおりです。

• 教育を受ける期間が 1 年増えるごとに、世帯の総収入は平均1,500.24 ドル増加します (労働時間が一定であると仮定)。
• 週あたりの労働時間が追加されるごとに、世帯の総収入は平均400.34 ドル増加します (教育年数が一定であると仮定)。

このモデルを使用すると、経済学者は教育レベルと総労働時間の増加が世帯収入の増加に関連していることをすぐに理解できます。

また、追加の教育や追加の労働時間が世帯収入にどのような影響を与えるかを正確に定量化することもできます。

理由4：経済動向の予測

統計は経済学でも傾向予測の形で使用されます。

たとえば、経済学者は、特定の国の商品の総売上高 (数百万単位) に関するデータを収集し、将来の売上予測を作成できます。

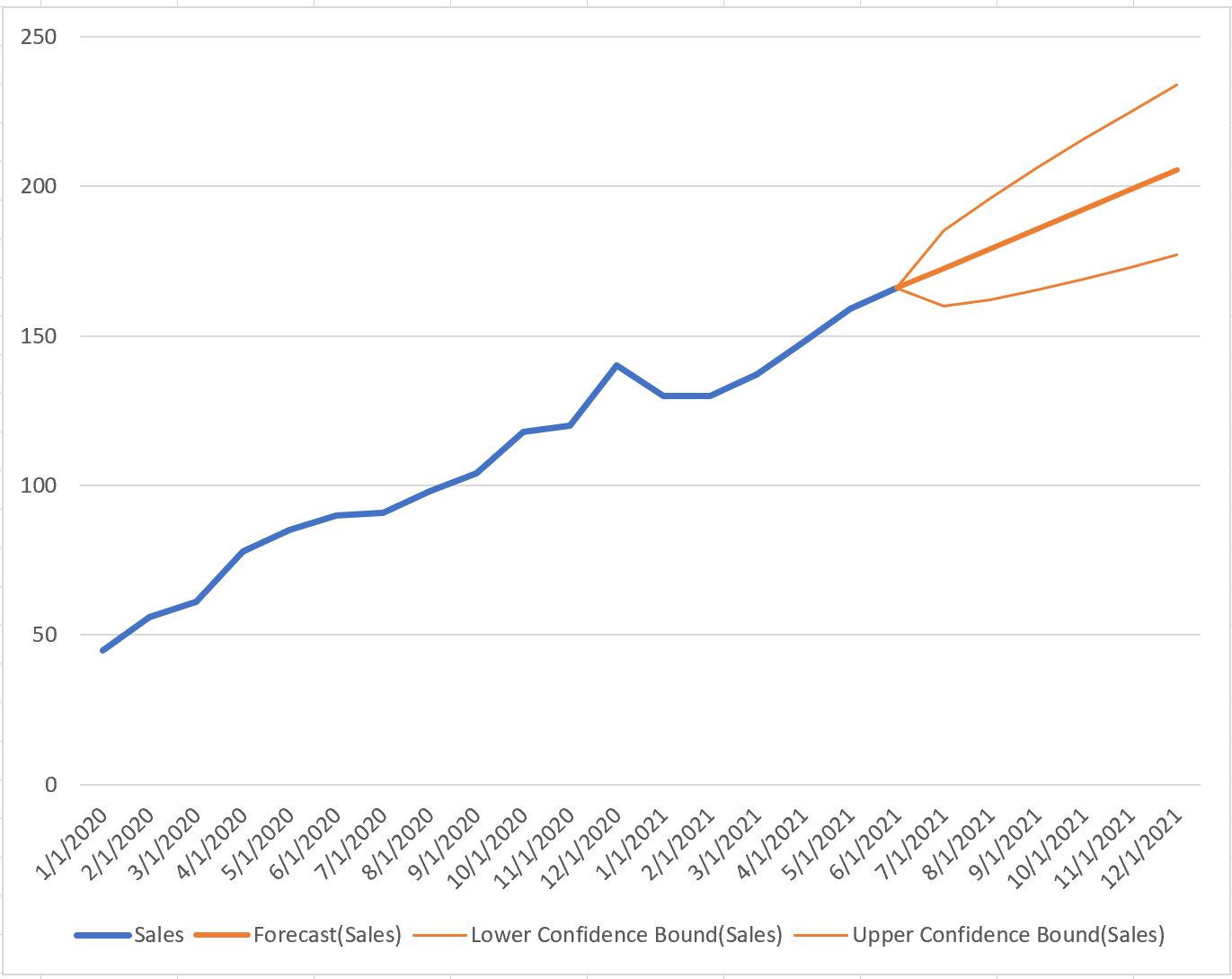
これらの予測により、経済学者は経済が今後数か月、数年でどのように推移するかを (ある程度の自信を持って) 予測できます。

追加リソース

次の記事では、他の分野における統計の重要性について説明しています。

なぜ統計が重要なのでしょうか? (統計が重要である 10 の理由!)
ビジネスにおける統計の重要性
会計における統計の重要性
教育における統計の重要性
医療における統計の重要性