グループ化されたデータの範囲を見つける方法: 例付き

何らかの方法でグループ化されたデータの範囲を計算したいことがよくあります。

範囲はデータセット内の最大値と最小値の差を表すことに注意してください。

たとえば、次のようなグループ化されたデータがあるとします。

生データの値がわからないため、正確な範囲を計算することはできませんが、次の式のいずれかを使用して範囲を推定することは可能です。

式 1: 上限と下限を使用する

グループ化されたデータ範囲 = U _max – L _min

金：

• U : 最大間隔の上限値
• L : 最小間隔の下限値

式 2: 中間点を使用する

グループ化されたデータ範囲 =_最大中間点 –_最小中間点

金：

• _Max Mid : 最大間隔の中間点
• Middle _min : 最小間隔の中点

次の例は、実際に各式を使用する方法を示しています。

例 1: グループ化されたデータ範囲を計算する

特定のクラスの 40 人の生徒によって採点された試験を示す次の度数分布があるとします。

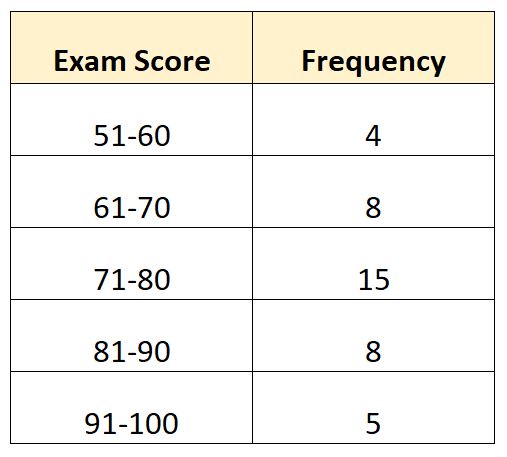
各式を使用して、このグループ化されたデータの範囲を計算する方法は次のとおりです。

式 1: 上限と下限を使用する

• グループ化されたデータ範囲 = U _max – L _min
• グループ化されたデータ範囲 = 100 – 51
• グループ化されたデータ範囲 = 49

この式を使用すると、範囲は49と推定されます。

式 2: 中間点を使用する

• グループ化されたデータ範囲 =_最大中間点 –_最小中間点
• グループ化されたデータ範囲 = (100+91)/2 – (60+51)/2
• グループ化されたデータ範囲 = 95.5 – 55.5
• グループ化されたデータ範囲 = 40

この式を使用すると、範囲は40と推定されます。

例 2: グループ化されたデータ範囲を計算する

60 人のバスケットボール選手が 1 試合ごとに獲得した得点数を示す次の度数分布があるとします。

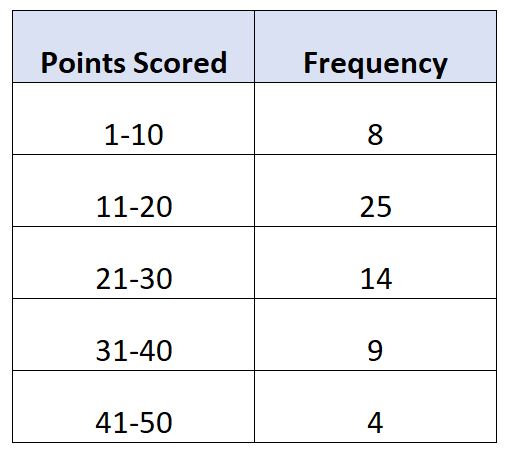
各式を使用して、このグループ化されたデータの範囲を計算する方法は次のとおりです。

式 1: 上限と下限を使用する

• グループ化されたデータ範囲 = U _max – L _min
• グループ化されたデータ範囲 = 50 – 1
• グループ化されたデータ範囲 = 49

この式を使用すると、範囲は49と推定されます。

式 2: 中間点を使用する

• グループ化されたデータ範囲 =_最大中間点 –_最小中間点
• グループ化されたデータ範囲 = (50+41)/2 – (1+10)/2
• グループ化されたデータ範囲 = 45.5 – 5.5
• グループ化されたデータ範囲 = 40

この式を使用すると、範囲は40と推定されます。

追加リソース

次のチュートリアルでは、グループ化されたデータを使用して他の一般的な操作を実行する方法について説明します。

グループ化されたデータの平均と標準偏差を見つける方法
グループ化されたデータの中央値を見つける方法
グループ化されたデータの分散を見つける方法
グループ化されたデータのパーセンタイル ランキングを計算する方法