管理限界
この記事では、管理限界とは何か、また管理図のさまざまな管理限界とは何かについて説明します。また、管理限界の計算方法や、プロセスの管理限界を決定する実際の例もご覧いただけます。
管理限界とは何ですか?
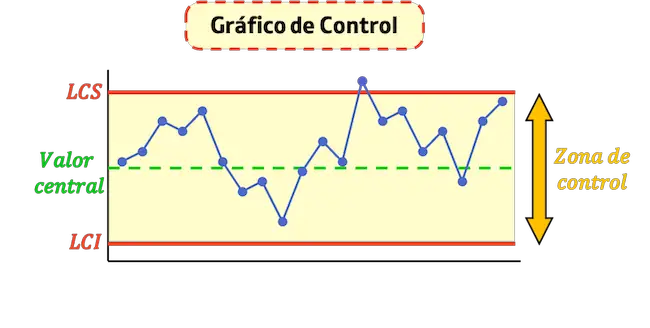
管理限界は、プロセスが管理されているかどうかを判断するために使用される管理図上の水平線です。
管理図には 2 つの管理限界があります。上限管理限界と下限管理限界は、それぞれ上と下の管理領域の境界を定めます。
したがって、管理限界は、プロセスの管理範囲を示すために使用される値です。プロセスから得られた測定値が管理限界内にある場合、それはプロセスが管理されていることを意味します。そうでない場合は、逸脱している可能性があるため、マシンまたはプロセスをチェックする必要があります。
管理限界の種類
管理限界は次のとおりです。
- 上限管理限界 (LCS) : これは、プロセスで受け入れられる最大値を示す線です。
- 下限管理限界 (LCI) : これは、プロセスで許容される最小値を示す線です。
- 中央管理線:グラフの平均値を表す線です。点がこの線に近づくほど、プロセスはより安定します。
管理限界の計算方法
現在、プロセスの制御限界は一般に、プロセスの制御を可能にするコンピュータ ソフトウェアによって計算されます。ただし、手動で見つける必要がある場合があるため、計算方法を理解しておくことも重要です。
管理図の管理限界の計算は、平均管理図か範囲管理図かによって値が変わるため、作成する管理図の種類によって異なります。
平均管理図は、プロセスの平均の推移を評価するグラフです。したがって、一連の値の平均は次の式を使用して計算されます。

金:
-

は小節番号 i です。
-

は取得された測定の数です。
平均に対する管理図の中心値を次のように指定します。
![]()
、これはサンプルの平均であり、次の式で計算されます。

金:
-
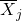
はサンプル j の平均です。
-

は採取されたサンプルの数です。
対照的に、範囲管理図の中心値は、取得されたすべてのサンプルの範囲の平均です。

金:
-
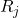
はサンプル j の範囲です。
-

は採取されたサンプルの数です。
したがって、管理図の管理限界を計算する式は次のとおりです。
コントロールカード
![Rendered by QuickLaTeX.com \begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-fea27f2cb07784e5d8f7e128a010a02c_l3.png)
Rコントロールカード
![Rendered by QuickLaTeX.com \begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5d3cf71032f18cd8710d9a2165d8daac_l3.png)
パラメータ A 2 、D 3および D 4の値は次の表に示されています。
| サイズ(号) | 2時 | 3日目 | J4 |
|---|---|---|---|
| 2 | 1,880 | 0.000 | 3,267 |
| 3 | 1,023 | 0.000 | 2,575 |
| 4 | 0.729 | 0.000 | 2,282 |
| 5 | 0.577 | 0.000 | 2,115 |
| 6 | 0.483 | 0.000 | 2004年 |
| 7 | 0.419 | 0.076 | 1,924 |
| 8 | 0.373 | 0.136 | 1,864 |
| 9 | 0.337 | 0.184 | 1,816 |
| 十 | 0.308 | 0.223 | 1,777 |
管理限界の計算例
ある産業会社は、製造プロセスが管理されているかどうかを確認するために、シリンダーの直径の測定を管理したいと考えています。これを行うには、15 分ごとに 5 つのシリンダーのサンプルを採取し、その直径を測定します。次の表に測定記録を示します。

管理限界を見つけるには、まず各測定セットの算術平均と範囲を取得する必要があります。

次に、平均と範囲の平均を計算しましょう。これは、それぞれ平均と範囲の管理図の中心値になります。


この場合、各サンプルは 5 つの測定値で構成されているため、管理限界式の係数は次のようになります。
![]()
![]()
![]()
平均管理図と拡張管理図の上限管理限界と下限管理限界を計算します。
管理図の管理限界
![Rendered by QuickLaTeX.com \begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c36f6b368a9a737de0ad139fd3a3953c_l3.png)
の管理限界 Rコントロールカード
![Rendered by QuickLaTeX.com \begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4f60f6739025a68d8e145d789bf3edea_l3.png)
したがって、運動制御カードは次のとおりです。


最初の管理図では、2 つの値が管理下限値を下回っていることがわかります。また、第2管理図では、管理上限値を超える値も存在する。したがって、プロセスは制御されません。