グループ化されたデータの四分位を計算する方法

四分位数は、データセットを 4 つの等しい部分に分割する値です。

次の式を使用して、グループ化されたデータの四分位を計算できます。

Q _i = L + (C/F) * (iN/4 – M)

金：

• L : i 番目の^四分位を含む区間の下限
• C : クラスの幅
• F : i 番目の^四分位を含む区間の頻度
• N : 合計周波数
• M : i 番目の^四分位を含む区間に至る累積度数

次の例は、この公式を実際に使用する方法を示しています。

例: グループ化されたデータの四分位数を計算する

次の頻度分布があるとします。

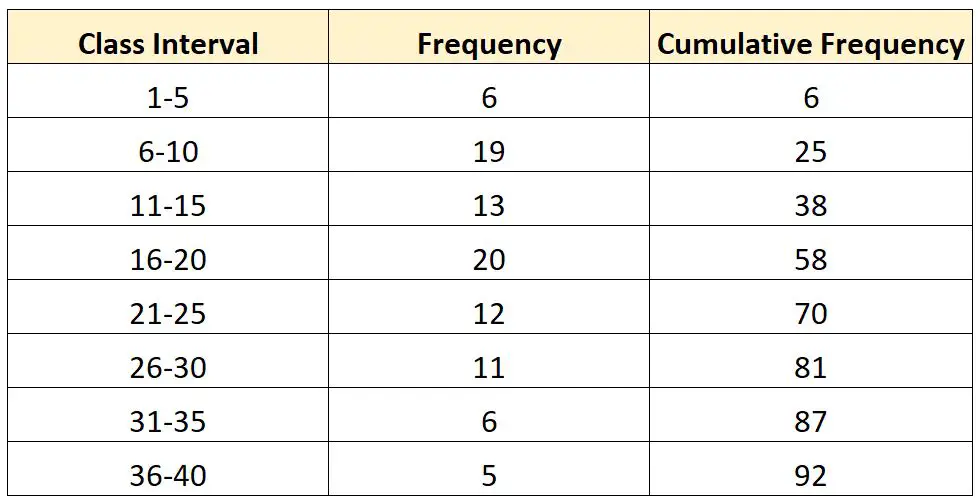
ここで、この分布の第 3 四分位 (Q ₃ ) の値を計算するとします。

第 3 四分位の値は、分布内の位置 (iN/4) に位置します。

したがって、(iN/4) = (3*92/4) = 69 となります。

69 は累積頻度 58 と 70 の間にあるため、第 3 四分位を含む間隔は間隔21 ～ 25になります。

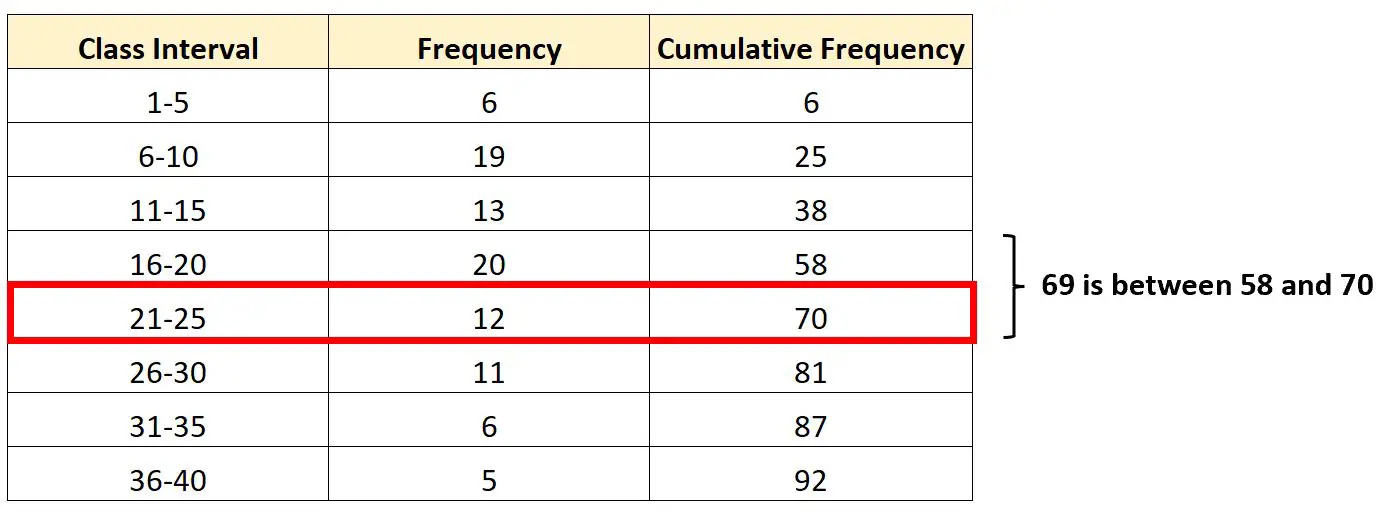
これを知ることで、式に組み込む必要な値をそれぞれ見つけることができます。

L : i 番目の^四分位を含む区間の下限

• 間隔の下限は21です。

C : クラスの幅

• クラスの幅は次のように計算されます: 25 – 21 = 4 。

F : i 番目の^四分位を含む区間の頻度

• クラス 21 ～ 25 の度数は12

N : 合計周波数

• 表内の累積頻度の合計は92です。

M : i 番目の^四分位を含む区間に至る累積度数

• クラス 21 ～ 25 までの累積度数は58です。

次に、これらすべての値を前の式に代入して、第 3 四分位の値を見つけることができます。

• Q _i = L + (C/F) * (iN/4 – M)
• Q ₃ = 21 + (4/12) * ((3)(92)/4 – 58)
• _{第 3 四半期}= 24.67

第 3 四分位の値は24.67です。

同様のアプローチを使用して、第 1 四分位値と第 2 四分位値を計算できます。

追加リソース

次のチュートリアルでは、グループ化されたデータの操作に関する追加情報を提供します。

グループ化されたデータの平均と標準偏差を見つける方法
グループ化されたデータモードを見つける方法
グループ化されたデータの中央値を見つける方法
グループ化またはグループ化されていない度数分布