連続変数とカテゴリ変数間の相関を計算する方法

2 つの連続変数間の相関を計算する場合、通常は ピアソン相関係数を使用します。

ただし、連続変数とカテゴリ変数の間の相関を計算したい場合は、いわゆる点双系列相関を使用できます。

点双直列相関は、バイナリ カテゴリ変数 (2 つの値のみを取る変数) と連続変数の間の相関を計算するために使用され、次のプロパティがあります。

• 点と双系列の相関は、-1 から 1 の間で変化します。
• バイナリ変数によって作成された各グループについて、連続変数は等しい分散で正規分布すると仮定されます。
• バイナリ変数によって作成された各グループには、極端な外れ値はないと想定されます。

次の例は、実際に点双直列相関を計算する方法を示しています。

例: 点-双系列相関の計算

大学教授が、性別と特定の資格試験のスコアとの間に相関関係があるかどうかを判断したいとします。

彼は、クラス内の 12 人の男子と 12 人の女子に関する次のデータを収集します。

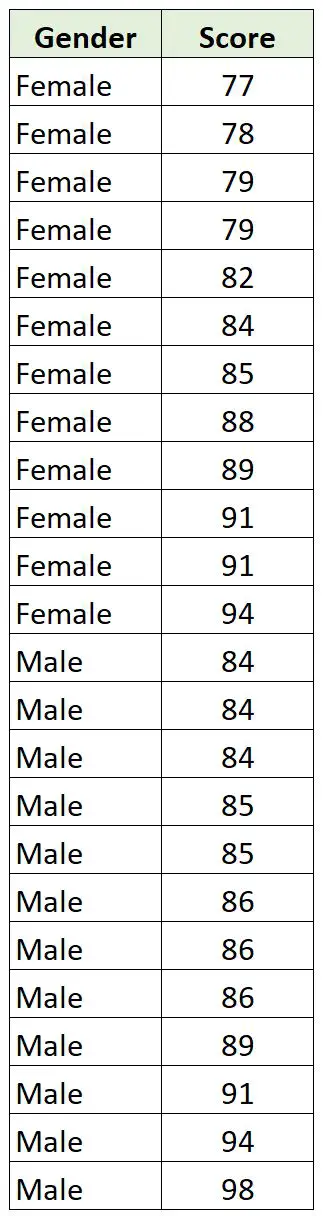
性別はカテゴリ変数であり、スコアは連続変数であるため、2 つの変数間の点双系列相関を計算することは理にかなっています。

教授は、任意の統計ソフトウェア (Excel、R、Python、SPSS、Stata など) を使用して、2 つの変数間の点双系列相関を計算できます。

次のコードは、性別変数の女性を表す値 0 と男性を表す値 1 を使用して、R で点双系列相関を計算する方法を示しています。

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

結果から、点双直列相関係数は0.281で、対応する p 値は0.1833であることがわかります。

相関係数は正であるため、性別とスコアの間に正の相関があることがわかります。

男性を 1、女性を 0 としてコード化したので、これは、スコアが男性の方が高くなる傾向があることを示しています (つまり、性別が「増加」するにつれてスコアが増加する傾向にあります)。 » 0 から 1)。

ただし、p 値は 0.05 以上であるため、この相関係数は統計的に有意ではありません。

追加リソース

次のチュートリアルでは、さまざまな統計ソフトウェアを使用して点の双系列相関を計算する方法を説明します。

Excelで点双系列相関を計算する方法
R で点双系列相関を計算する方法
Python で点と双系列の相関を計算する方法