コイントスで少なくとも 1 つの表が出る確率を見つける方法

特定のコイントスで表が出る確率は 1/2 または 0.5 です。

特定の回数のコイントスで少なくとも 1 つの表が出る確率を求めるには、次の式を使用できます。

P(少なくとも 1 つのヘッド) = 1 – 0.5 ⁿ

金：

• n : 総反転回数

たとえば、コインを2回投げたとします。

これら 3 回のスロー中に少なくとも 1 つの表が得られる確率は次のとおりです。

• P(少なくとも 1 つのヘッド) = 1 – 0.5 ⁿ
• P(少なくとも 1 つのヘッド) = 1 – 0.5 ³
• P (少なくとも 1 つのヘッド) = 1 – 0.125
• P(少なくとも 1 つのヘッド) = 0.875

この答えは、コインを 2 回投げた場合に考えられるすべての結果をリストし、「T」が表、「H」が裏を表す場合に意味が生じます。

• TT
• TTH
• THH
• THT
• ふふふ
• VRD
• HTH
• HTT

8 つの可能な結果のうち 7 つに少なくとも 1 つの表 (H) が表示されることに注意してください。これは 7/8 = 0.875に相当します。

または、コインを 5 回投げるとします。

これら 5 回のスロー中に少なくとも 1 つの表が得られる確率は次のとおりです。

• P(少なくとも 1 つのヘッド) = 1 – 0.5 ⁿ
• P(少なくとも 1 つのヘッド) = 1 – 0.5 ⁵
• P(少なくとも 1 つのヘッド) = 1 – 0.25
• P(少なくとも 1 つのヘッド) = 0.96875

次の表は、さまざまな回数のコイントスで少なくとも 1 つの表が出る確率を示しています。

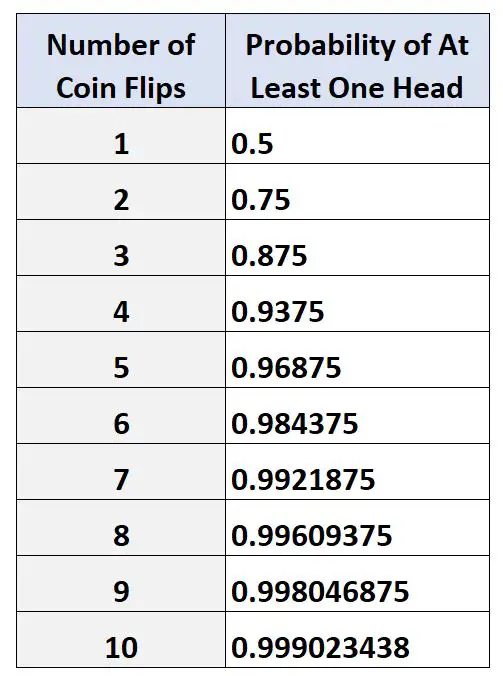
コイントスの回数が多いほど、少なくとも 1 つの表が得られる確率が高くなることに注意してください。

コインを複数回投げ続けると、最終的に表が現れる確率が高くなるはずであることを考えると、これは理にかなっています。

追加リソース

次のチュートリアルでは、その他の一般的な確率関連の計算を実行する方法について説明します。

「少なくとも 1 回」成功する確率を見つける方法
「少なくとも 2 回」成功する確率を見つける方法
AとBの確率を求める方法
A または B の確率を求める方法