複製ありまたはなしの anova: 違いは何ですか?
二元配置分散分析は、 2 つの予測変数 (または「因子」) が応答変数に統計的に有意な影響を与えるかどうかを判断するために使用されます。
二元配置分散分析モデルには 2 つの異なるタイプがあります。
1. 複製を行わない二元配置分散分析
- 予測子変数のレベルの組み合わせごとに、観測値は 1 つだけ存在します。
2. レプリケーションを使用した二元配置分散分析
- 予測子変数のレベルの組み合わせごとに、複数の観測値が存在します。
たとえば、植物学者は、日光への曝露 (なし、低、中、高) と水やりの頻度 (毎日、毎週) が植物の成長に統計的に有意な影響を与えるかどうかを知りたい場合があります。
彼女は、次の二元配置分散分析モデルのいずれかを実行できます。
1. 複製を行わない二元配置分散分析
このアプローチを使用すると、植物学者は日光レベルと水やりの頻度の組み合わせごとに植物の成長を測定するだけになります。
たとえば、日光にさらされず、毎日水を与えられなかった植物の成長を測定しました。
次に、彼女は日光にさらさず、毎週水を与えずに単一の植物の成長を測定しました。
等々。
次の表は、レプリケーションを使用しない二元配置分散分析がどのようになるかを示しています。
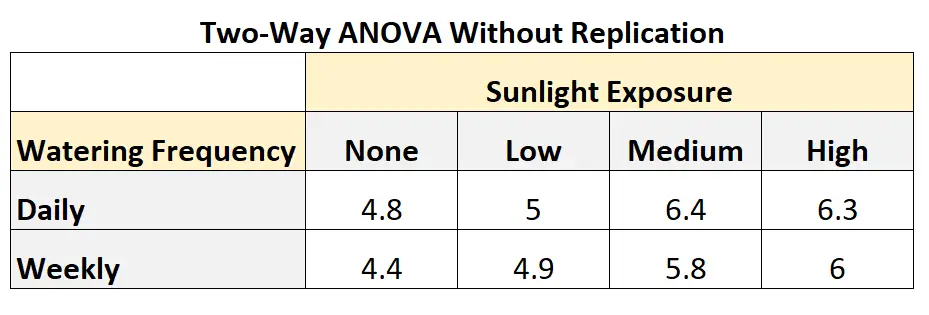
表から次のことがわかります。
- 日光にさらさず、毎日水を与えたこの植物は、 4.8インチに成長しました。
- 日光にさらさず、毎週水やりをしなかった植物は、 4.4インチ成長しました。
- 日光への曝露を少なくし、毎日水やりをした植物は5インチ成長しました。
- 日光への露出を低くし、毎週水を与えたこの植物は、 4.9インチ成長しました。
等々。
2. レプリケーションを使用した二元配置分散分析
このアプローチを使用して、植物学者は、日光レベルと水やりの頻度の組み合わせごとに複数の植物の成長を測定します。
たとえば、日光にさらされず、毎日水を与えられない 5 つの異なる植物の成長を測定できます。
次に、彼女は日光にさらさず、毎週水やりをせずに、他の 5 つの植物の成長を測定しました。
等々。
次の表は、レプリケーションを使用した二元配置分散分析がどのようになるかを示しています。
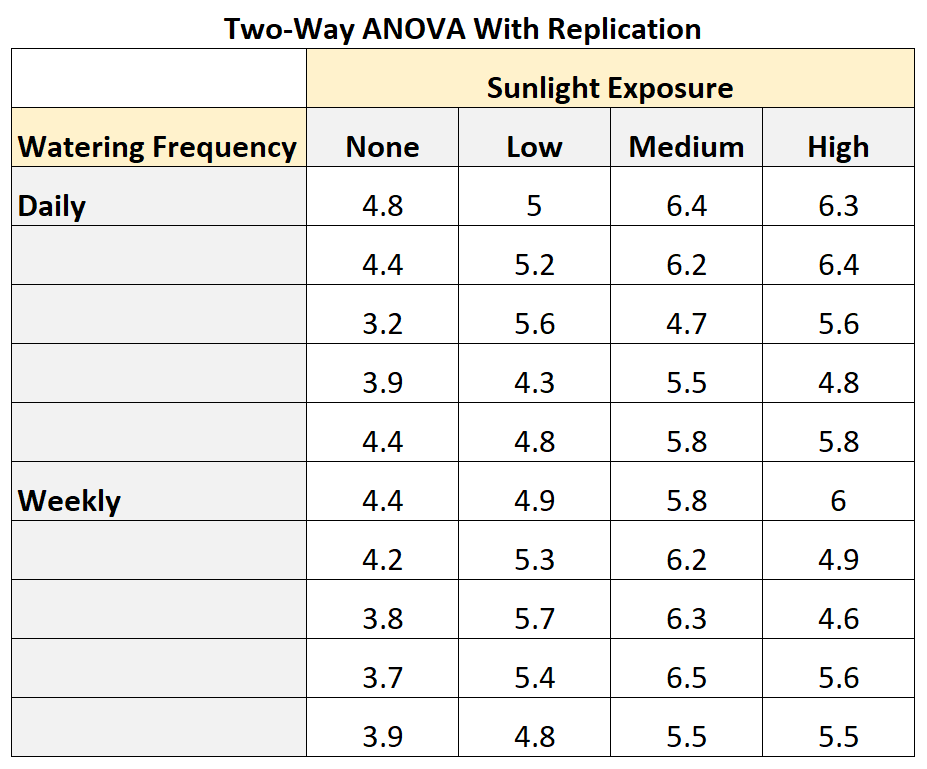
表から次のことがわかります。
- 日光にさらさず、毎日水やりをしなかった植物は、 4.8インチ成長しました。
- 日光にさらさず、毎日水を与えなかった別の植物は、 4.4インチまで成長しました。
- 日光にさらさず、毎日水を与えなかった別の植物は、 3.2インチ成長しました。
等々。
複製ありとなしの ANOVA の違い
複製を使用した ANOVA モデルと複製を使用しない ANOVA モデルの最大の違いは、複製を使用した ANOVA では 2 つの予測子変数間の交互作用効果のみを測定できることです。
交互作用効果とは、2 つの予測変数間にある種の相互作用が存在することを意味し、これは、予測変数と応答変数の間の関係の解釈方法に影響を与える可能性があります。
たとえば、植物学者は、日光への曝露と水やりの頻度が植物の成長に影響を与えるかどうかを知りたいと思うかもしれません。
これら 2 つの予測変数が植物の成長に影響を与える可能性はありますが、相互作用する可能性もあります。
たとえば、日光への曝露により、植物に毎日水を与えるか毎週水を与えるかに応じて、植物の成長速度が異なる可能性があります。
この場合、日光への曝露と水やりの頻度の間には相互作用効果があります。
ただし、交互作用効果を測定する唯一の方法は、予測変数のレベルの組み合わせごとに複数の測定値を用意することです。
Excel でレプリケーションを使用した場合と使用しない場合の ANOVA
Excel でレプリケーションを行わずに二元配置分散分析を実行すると、結果は次のようになります。
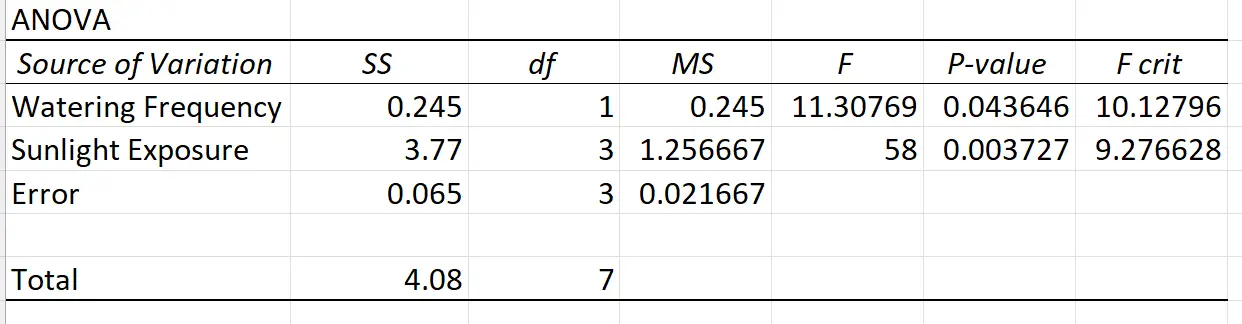
太陽光への曝露と水やりの頻度に関する ANOVA 表の p 値は 0.05 未満であるため、両方の変数が植物の成長に統計的に有意な影響を与えていると結論付けることができます。
ただし、ANOVA 表には交互作用項が含まれていないため、2 つの予測子変数間に交互作用効果があるかどうかはわかりません。
一方、 Excel でレプリケーションを使用して二元配置分散分析を実行すると、結果は次のようになります。
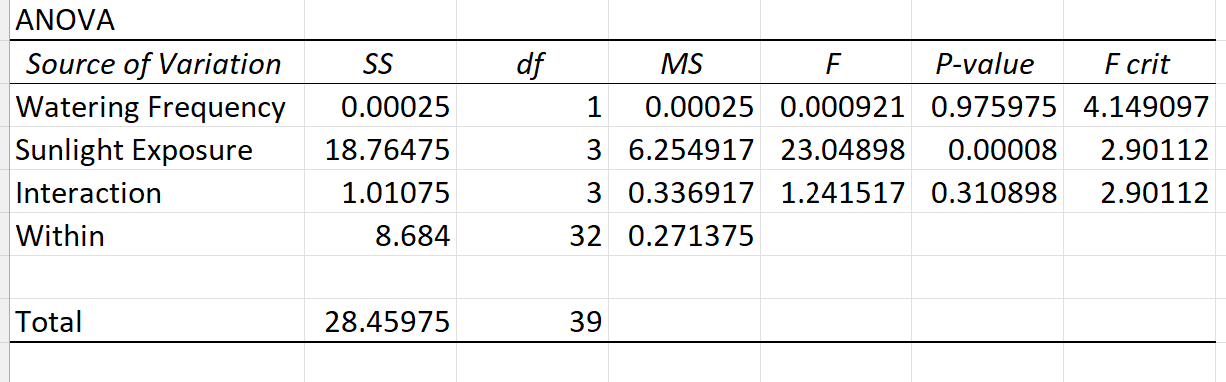
この ANOVA テーブルには、日光への曝露、水やりの頻度、およびこれら 2 つの予測変数間の相互作用効果の p 値が含まれていることに注意してください。
表から、水やりの頻度は統計的に有意ではなく、日光への曝露は統計的に有意であり、統計的に有意ではない 2 つの予測変数間に相互作用効果はないことがわかります。
これは、水やりの頻度に関係なく、植物の成長に対する日光曝露の影響について結論を導くことができることを意味します。
追加リソース
次のチュートリアルでは、二元配置 ANOVA モデルに関する追加情報を提供します。