実験確率

ここでは、実験確率の意味と実験確率の計算方法を説明します。さらに、実験確率を計算する段階的な解決例を確認できます。

実験確率とは何ですか?

実験確率とは、実験の結果や経験的事実に基づいた統計的な尺度であり、事象が発生する確率を示します。

さらに、実験を繰り返すほど、得られる実験確率はより正確になります。このため、実験の確率を決定するために、数千の実験を迅速にシミュレートできるコンピューター プログラムが一般的に使用され、より高い精度が得られます。

実験確率は、経験確率または頻度確率とも呼ばれます。

実験確率は 0 から 1 までの数値です。論理的には、イベントの実験確率の値が大きいほど、そのイベントが発生する可能性が高く、その逆の値が小さいほど、イベントが発生する可能性は低くなります。が発生する可能性があります。またはイベントが発生します。ただし、実験確率の値は常に 0 から 1 の間になります。

実験的な確率公式

実験確率の公式は、実験中にイベントが発生した回数を、実験が実行された合計回数で割ったものです。

たとえば、ある人がターゲットに向かって 10 本のダーツを投げ、なんとか中央に 6 本のダーツを当てることができた場合、その人がダーツの中央に当たる確率は次のように計算されます。

実験確率の例

実験確率の数学的定義を理解したら、このタイプの確率に関する段階的な演習を解いていきます。目的は、イベントの実験確率がどのように計算されるかを学ぶことです。質問がある場合は、コメントに書き込んでください。

• サイコロを振るランダム実験を構成する要素事象の実験確率を計算します。

実験確率を求める前に、得られた実験結果と理論結果を比較するために理論確率を計算します。ご存知のとおり、サイコロを振るときは 6 つの出目 (1、2、3、4、5、6) が考えられるため、各基本事象の理論上の確率は次のようになります。

この演習を解決するには、サイコロを振ることを数回シミュレートし、結果を分割表に記録する必要があります。今回は Excel プログラムを使用してシミュレーションを行いますが、もちろんお好みのプログラムを使用することもできます。

最初に 10 回のスロー、次に 100 回のスロー、最後に 1,000 回のスローをシミュレーションします。こうすることで、結果を分析し、実験のサンプルサイズに応じて結果がどのように変化するかを確認できます。 10 個のサイコロを投げるランダムなシミュレーション後に得られた結果は次のとおりです。

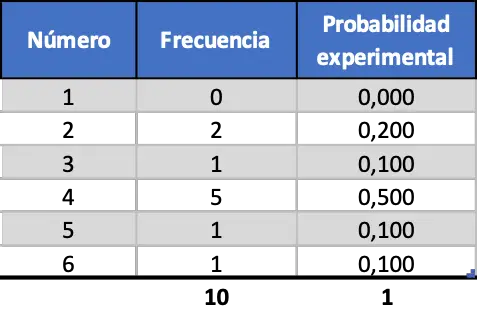
ご覧のとおり、得られた実験確率は、以前に計算された理論確率 (0.167) とは現時点では大きく異なります。

しかし、テストの数が増えるにつれて、これら 2 つの指標はより似てきます。100 回の打ち上げのシミュレーションを見てください。

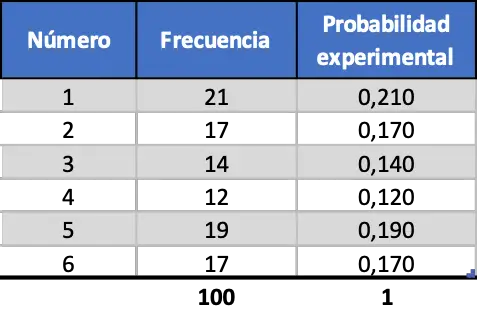
ここで、実験確率は理論確率値により似ていますが、依然として大幅に乖離した値が得られます。

最後に、同じ手順を実行しますが、1000 回の起動をシミュレートします。

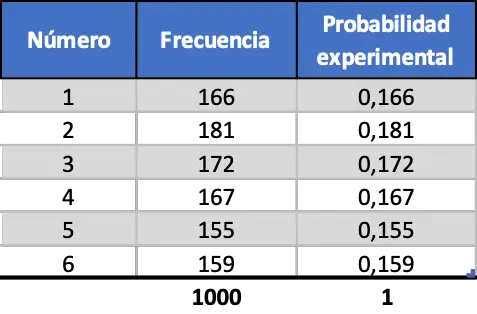
最後の分割表からわかるように、実験的確率の値は理論的確率と非常に似ています。

要約すると、実行される実験の数が増えるほど、イベントの実験確率の値は理論上の確率に近づきます。この法則は大数の法則として定義されており、データが多ければ多いほど、実験値が理論値に近づくことになります。

同様に、3 つの頻度表を比較すると、実験確率は決定的なものではなく、実行された実験の数に応じて変化することがわかります。つまり、取得した値を解釈する方法を知る必要があります。

実験確率と理論確率

実験確率と理論確率 (または古典確率) の違いは、実験確率は実際の実験から収集されたデータから計算されるのに対し、理論確率は実験を実行する必要なしに計算されることです。

これまで見てきたように、イベントの実験的確率を推定するには、多数の実験をシミュレートする必要があります。ただし、理論上の確率の計算には理論と論理が関係します。それがどのように行われるかはここで見ることができます: