Excelで重回帰を実行する方法

重線形回帰は、 2 つ以上の説明変数と応答変数の間の関係を理解するために使用できる方法です。

このチュートリアルでは、Excel で重回帰を実行する方法について説明します。

注:説明変数が 1 つだけの場合は、代わりに単純な線形回帰を実行する必要があります。

例: Excel での重線形回帰

勉強に費やした時間数と予備試験の受験数が、学生が特定の大学入学試験で取得する成績に影響するかどうかを知りたいとします。

この関係を調べるために、学習時間と受けた予備試験を説明変数として、試験結果を応答変数として使用して重線形回帰を実行できます。

重線形回帰を実行するには、Excel で次の手順を実行します。

ステップ 1: データを入力します。

20 人の学生の学習時間数、受験した予備試験、および受け取った試験結果に関する次のデータを入力します。

ステップ 2: 重回帰を実行します。

Excel の上部のリボンで[データ]タブに移動し、 [データ分析]をクリックします。このオプションが表示されない場合は、まず無料の Analysis ToolPak ソフトウェアをインストールする必要があります。

「データ分析」をクリックすると、新しいウィンドウが表示されます。 「回帰」を選択し、「OK」をクリックします。

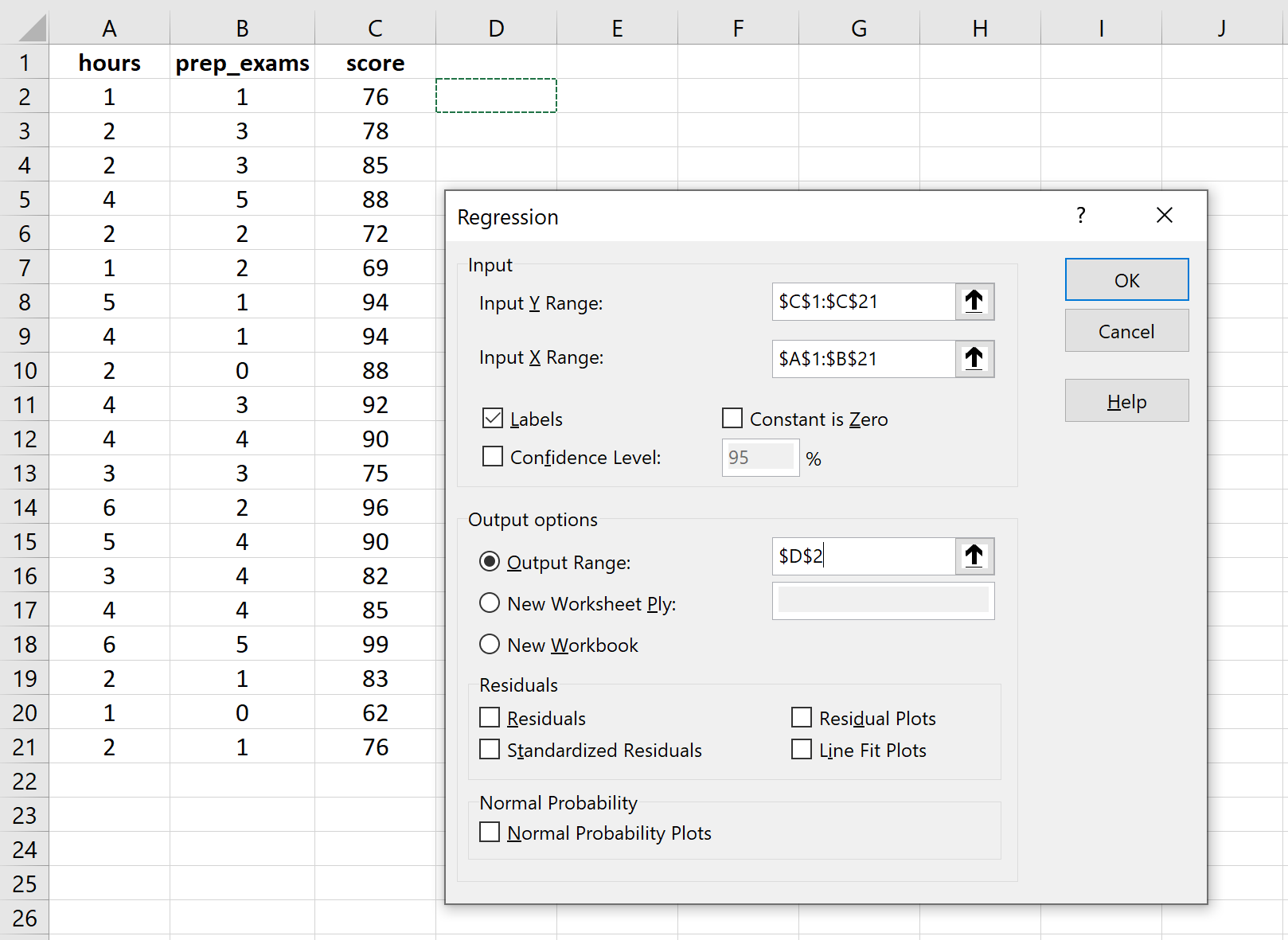
[入力 Y 範囲]に、応答変数の値の配列を入力します。 [入力 X 範囲]に、2 つの説明変数の値の配列を入力します。 [ラベル]の横にあるボックスをオンにして、入力範囲に変数名が含まれていることを Excel に知らせます。 [出力範囲]で、回帰出力を表示するセルを選択します。次に、 「OK」をクリックします。

次の出力が自動的に表示されます。

ステップ 3: 結果を解釈します。

結果内の最も関連性の高い数値を解釈する方法は次のとおりです。

R スクエア: 0.734 。これを決定係数といいます。説明変数によって説明できる応答変数の分散の割合です。この例では、試験得点の変動の 73.4% は、勉強時間数と受験した予備試験の数によって説明されます。

標準誤差: 5.366 。これは、観測値と回帰直線の間の平均距離です。この例では、観測値は回帰直線から平均して 5,366 単位外れています。

F: 午後 11:46これは回帰モデルの全体的な F 統計量であり、回帰 MS/残差 MS として計算されます。

意味 F: 0.0000 。これは、全体的な F 統計量に関連付けられた p 値です。これにより、回帰モデル全体が統計的に有意であるかどうかがわかります。言い換えれば、組み合わせた 2 つの説明変数が応答変数と統計的に有意な関連性を持っているかどうかがわかります。この場合、p 値は 0.05 未満であり、説明変数である学習時間と受けた予備試験の合計が試験結果と統計的に有意な関連性があることを示しています。

P 値。個々の p 値は、各説明変数が統計的に有意であるかどうかを示します。学習時間は統計的に有意 (p = 0.00) ですが、予備試験の受験時間(p = 0.52) は α = 0.05 で統計的に有意ではないことがわかります。過去の予備試験は統計的に有意ではないため、最終的にはモデルから削除することを決定する可能性があります。

係数:各説明変数の係数は、他の説明変数が一定のままであると仮定した場合、応答変数の予想される平均変化を示します。たとえば、受験した模擬試験が一定であると仮定すると、勉強に費やす時間がさらに 1 時間増えるごとに、試験の平均得点は5.56 点増加すると予想されます。

別の見方をすると、生徒 A と生徒 B が同じ回数の予備試験を受け、生徒 A が 1 時間長く勉強した場合、生徒 A の得点は生徒 B より5.56点高くなるはずです。

切片係数は、何時間も勉強せず、予備試験も受けなかった生徒の予想される試験スコアが67.67であることを意味すると解釈します。

推定回帰式:モデル出力の係数を使用して、次の推定回帰式を作成できます。

試験スコア = 67.67 + 5.56*(時間) – 0.60*(準備試験)

この推定回帰式を使用して、学習時間数と受験した模擬試験の数に基づいて、生徒の予想される試験スコアを計算できます。たとえば、3 時間勉強して予備試験を受ける学生は、 83.75の成績を取得する必要があります。

試験のスコア = 67.67 + 5.56*(3) – 0.60*(1) = 83.75

過去の予備試験は統計的に有意ではなかったので (p=0.52)、モデル全体に何の改善ももたらさないため、試験を削除することを決定する場合があることに注意してください。この場合、説明変数として調査時間のみを使用して単純な線形回帰を実行できます。

この単純な線形回帰分析の結果は、 ここにあります。

追加リソース

多重線形回帰を実行したら、次のようないくつかの仮定を確認することができます。

1. VIF を使用した多重共線性のテスト。

2. Breusch-Pagan 検定を使用して不均一分散性を検定します。

3. QQ プロットを使用して正規性をテストします。