反復測定 anova を手動で実行する方法
反復測定 ANOVA は、各グループに同じ被験者が含まれる 3 つ以上のグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
このチュートリアルでは、一元配置反復測定分散分析を手動で実行する方法について説明します。
例: 手動による一元配置反復測定分散分析
研究者は、3 つの異なる薬剤が異なる反応時間を引き起こすかどうかを知りたいと考えています。これをテストするために、各薬剤に対する 5 人の患者の反応時間 (秒単位) を測定しました。結果を以下に示します。
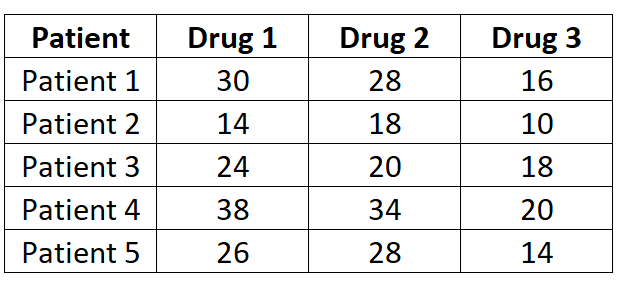
各患者は 3 つの薬剤のそれぞれについて測定されるため、一元配置反復測定分散分析を使用して、平均反応時間が薬剤間で異なるかどうかを判断します。
反復測定 ANOVA を手動で実行するには、次の手順に従います。
ステップ 1: SST を計算します。
まず、総平方和 (SST) を計算します。これは、次の式を使用して求められます。
SST = s 2合計(n合計-1)
金:
- s 2 total : データセットの分散
- n total : データセット内の観測値の合計数
この例では、SST を次のように計算します: (64.2667)(15-1) = 899.7
ステップ 2: SSB を計算する
次に、二乗和 (SSB) を計算します。これは、次の式を使用して求められます。
SSB = Σn j ( x j – x合計) 2
金:
- Σ : 「和」を意味するギリシャ語の記号
- n j : j番目のグループの観測値の総数
- x j : j 番目のグループの平均
- x total : すべてのデータの平均
この例では、SSB を次のように計算します: (5)(26.4-22.533) 2 +(5)(25.6-22.533) 2 + (5)(15.6-22.533) 2 = 362.1
ステップ 3: SSS を計算します。
次に、被験者の二乗和 (SSS) を計算します。これは、次の式を使用して求められます。
SSS =(Σr 2 k /c) – (N 2 /rc)
金:
- Σ : 「和」を意味するギリシャ語の記号
- r 2 k : k 番目の患者の二乗和
- N:すべてのデータの総計
- r:患者の総数
- c:グループの総数
この例では、SSS を次のように計算します: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441.1
ステップ 4: SES を計算します。
次に、二乗誤差和 (SSE) を計算します。これは、次の式を使用して求められます。
SSE = SST – SSB – SSS
この例では、SES を次のように計算します: 899.7 – 362.1 – 441.1 = 96.5
ステップ 5: 反復測定 ANOVA 表を完成させます。
SSB、SSS、SSE が得られたので、反復測定 ANOVA テーブルに値を入力できます。
| ソース | 二乗和 (SS) | DF | 平均二乗 (MS) | F |
|---|---|---|---|---|
| 間 | 362.1 | 2 | 181.1 | 15.006 |
| 主題 | 441.1 | 4 | 110.3 | |
| エラー | 96.5 | 8 | 12.1 |
表内のさまざまな数値を計算する方法は次のとおりです。
- df between: #groups – 1 = 3 – 1 = 2
- DF 件名: #参加者 – 1 = 5 – 1 = 4
- エラー df: df between * df subject = 2*4 = 8
- MS が入る: SSB / df が入る = 362.1 / 2 = 181.1
- MS サブジェクト: SSS サブジェクト / df = 441.1 / 4 = 110.3
- MS エラー: SSE エラー / df = 96.5 / 8 = 12.1
- F: MS 入力 / MS エラー = 181.1 / 12.1 = 15.006
ステップ 6: 結果を解釈します。
この一元配置反復測定 ANOVA の F 検定統計量は15.006です。これが統計的に有意な結果であるかどうかを判断するには、次の値を持つF 分布表にある臨界 F 値と比較する必要があります。
- α (有意水準) = 0.05
- DF1 (分子の自由度) = df between = 2
- DF2 (分母の自由度) = 誤差 df = 8
F の臨界値は4.459であることがわかります。
ANOVA 表の F 検定統計量は F 分布表の臨界値 F より大きいため、帰無仮説を棄却します。これは、薬剤の平均応答時間の間に統計的に有意な差があると言える十分な証拠があることを意味します。