Excel での曲線近似 (例付き)
Excel で一連のデータの曲線に最もよく適合する方程式を見つけたい場合があります。
幸いなことに、これは Excel のトレンドライン関数を使用して非常に簡単に実行できます。
このチュートリアルでは、Excel で方程式を曲線に当てはめる方法を段階的に説明します。
ステップ 1: データを作成する
まず、操作する偽のデータセットを作成しましょう。
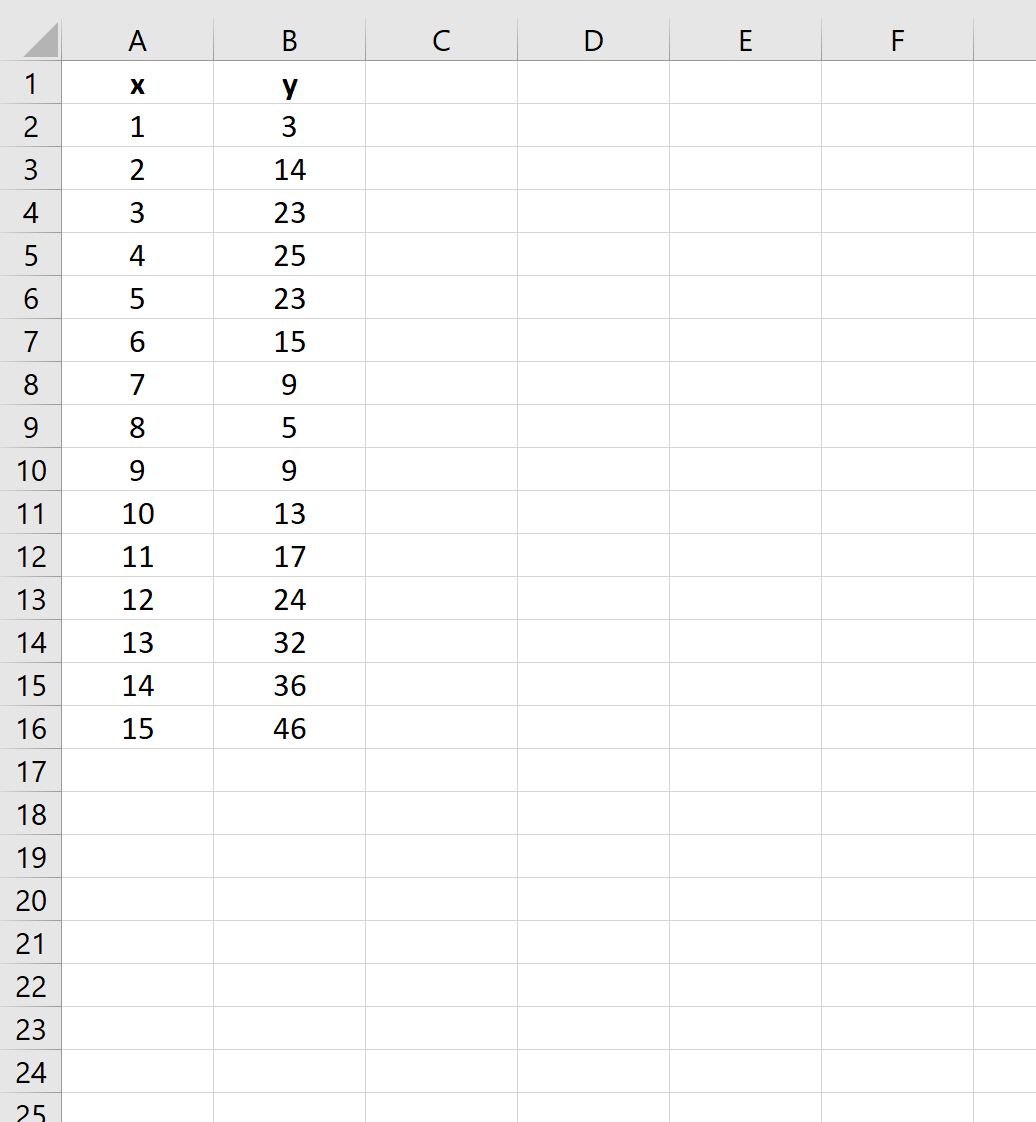
ステップ 2: 散布図を作成する
次に、散布図を作成してデータセットを視覚化しましょう。
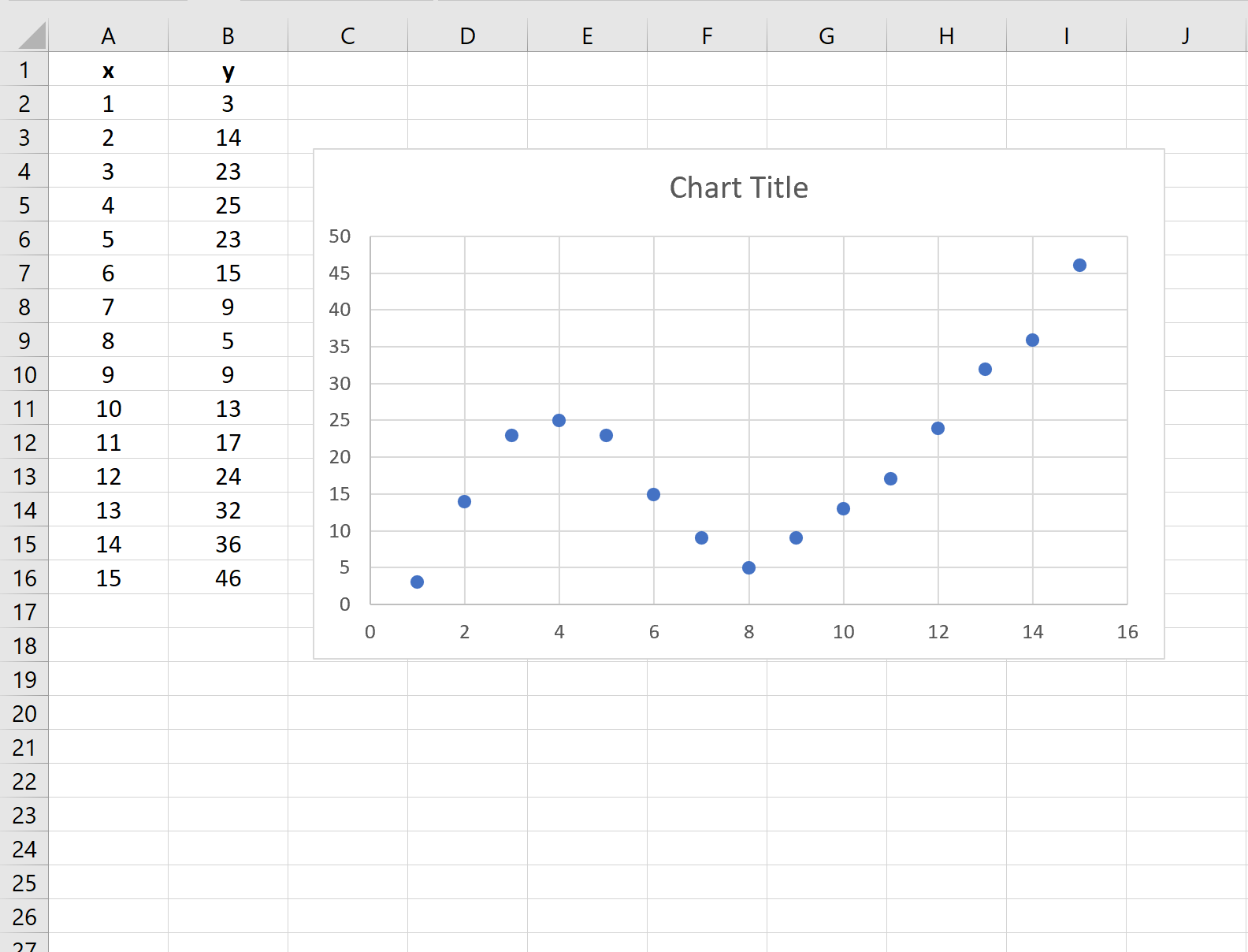
まず、次のようにセルA2:B16を強調表示します。
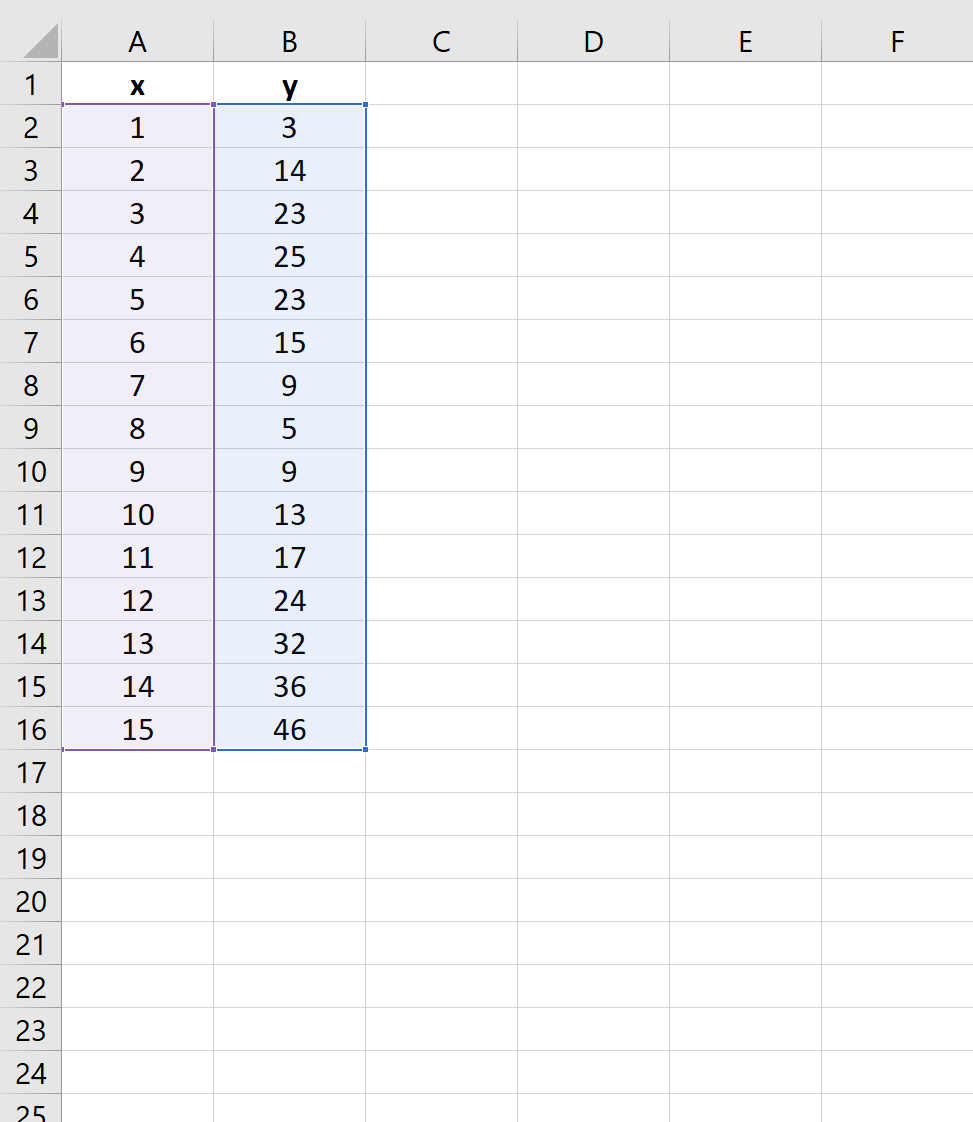
次に、上部のリボンに沿って[挿入]タブをクリックし、 [散布]の下にある最初のプロット オプションをクリックします。
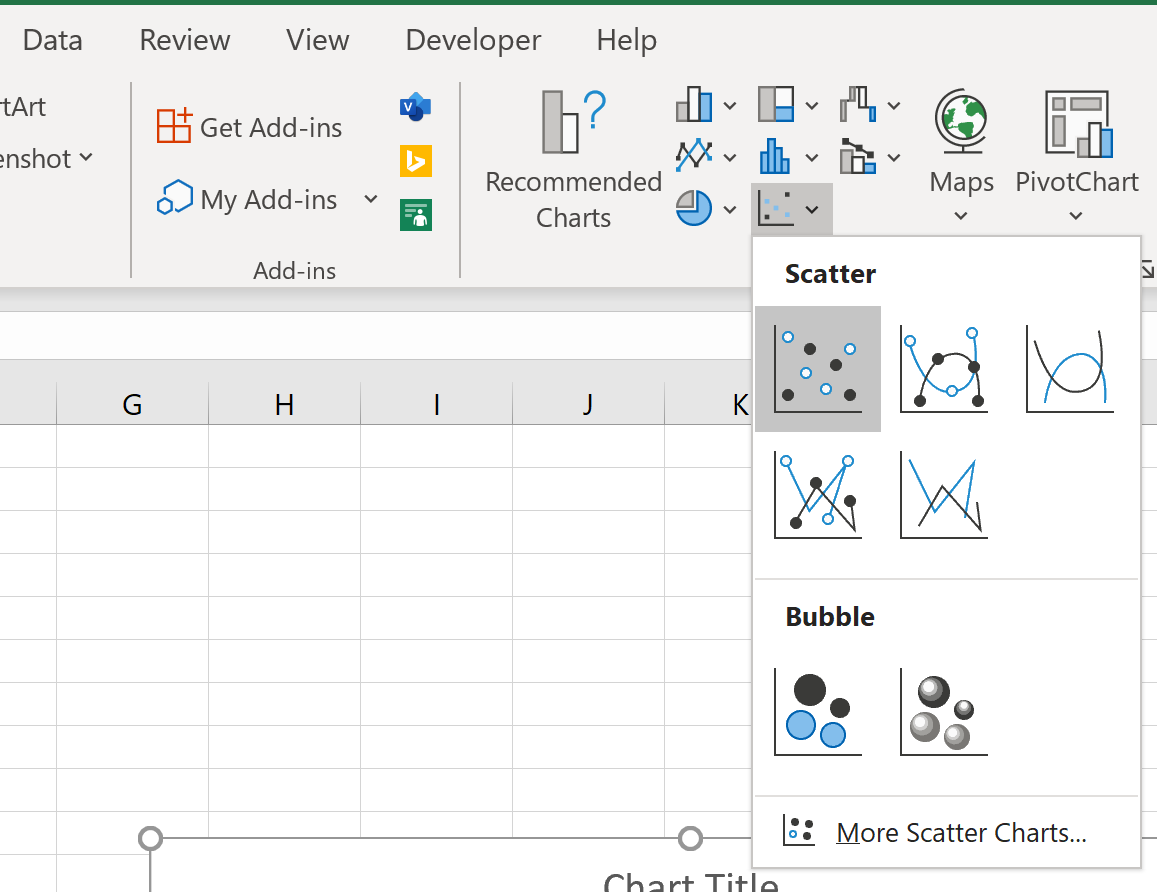
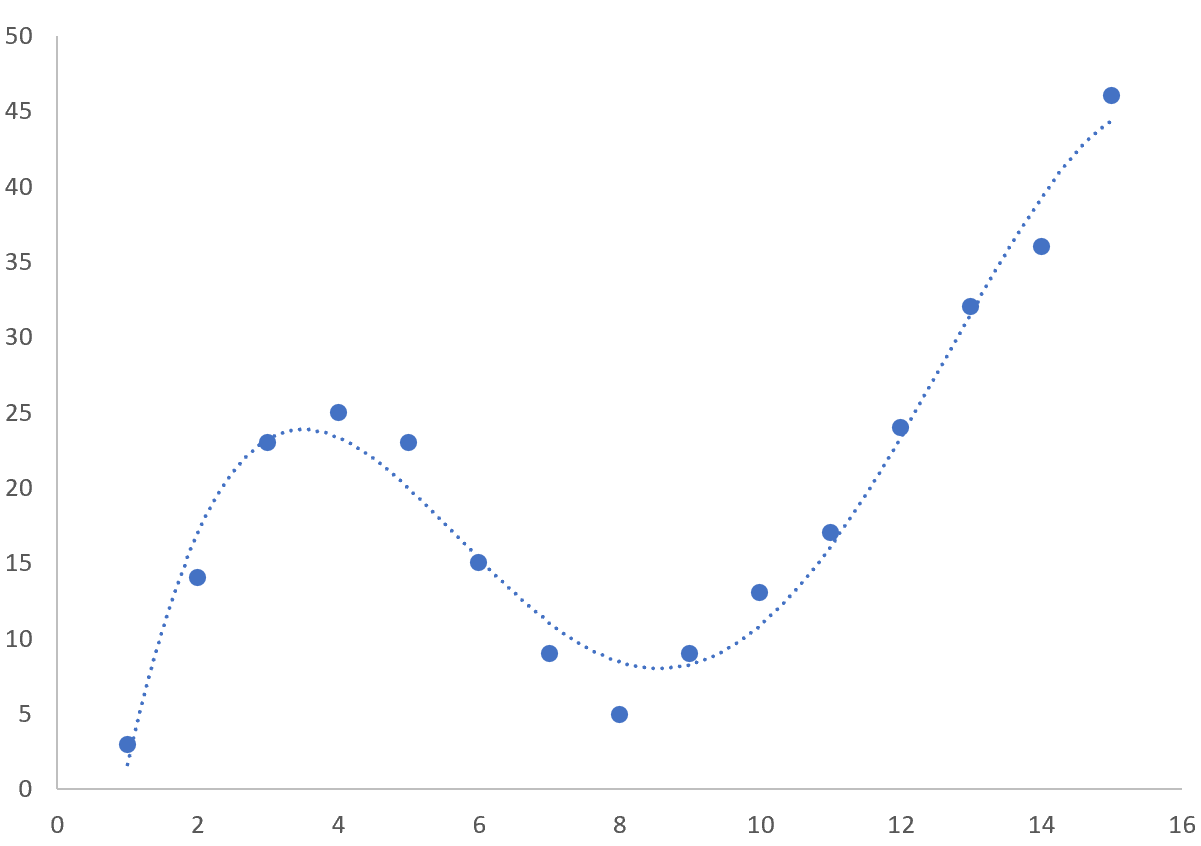
これにより、次の散布図が生成されます。
ステップ 3: 近似曲線を追加する
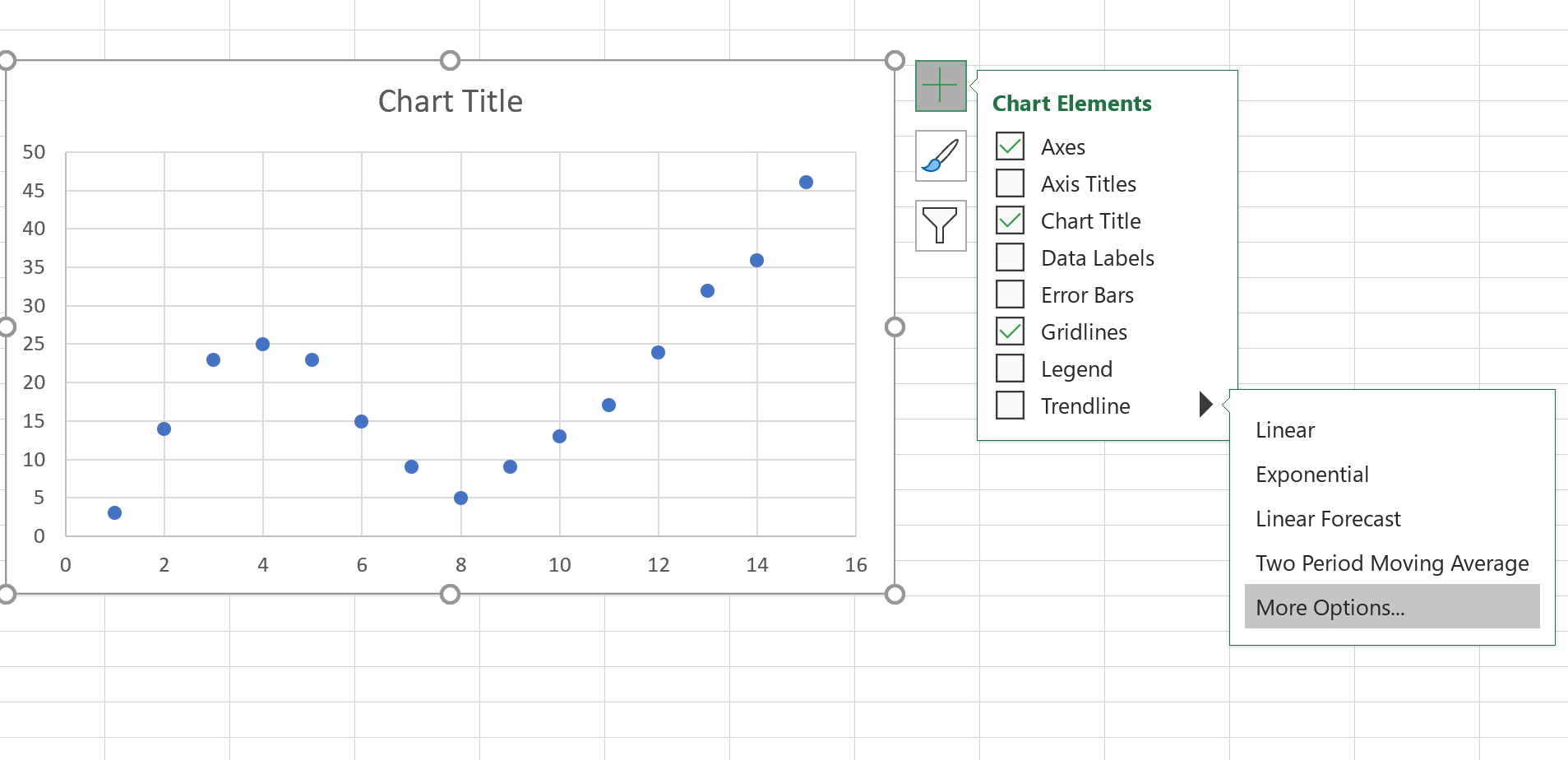
次に、散布図上の任意の場所をクリックします。次に、右上隅にある+記号をクリックします。ドロップダウン メニューで、 [トレンドライン]の横にある矢印をクリックし、 [その他のオプション]をクリックします。
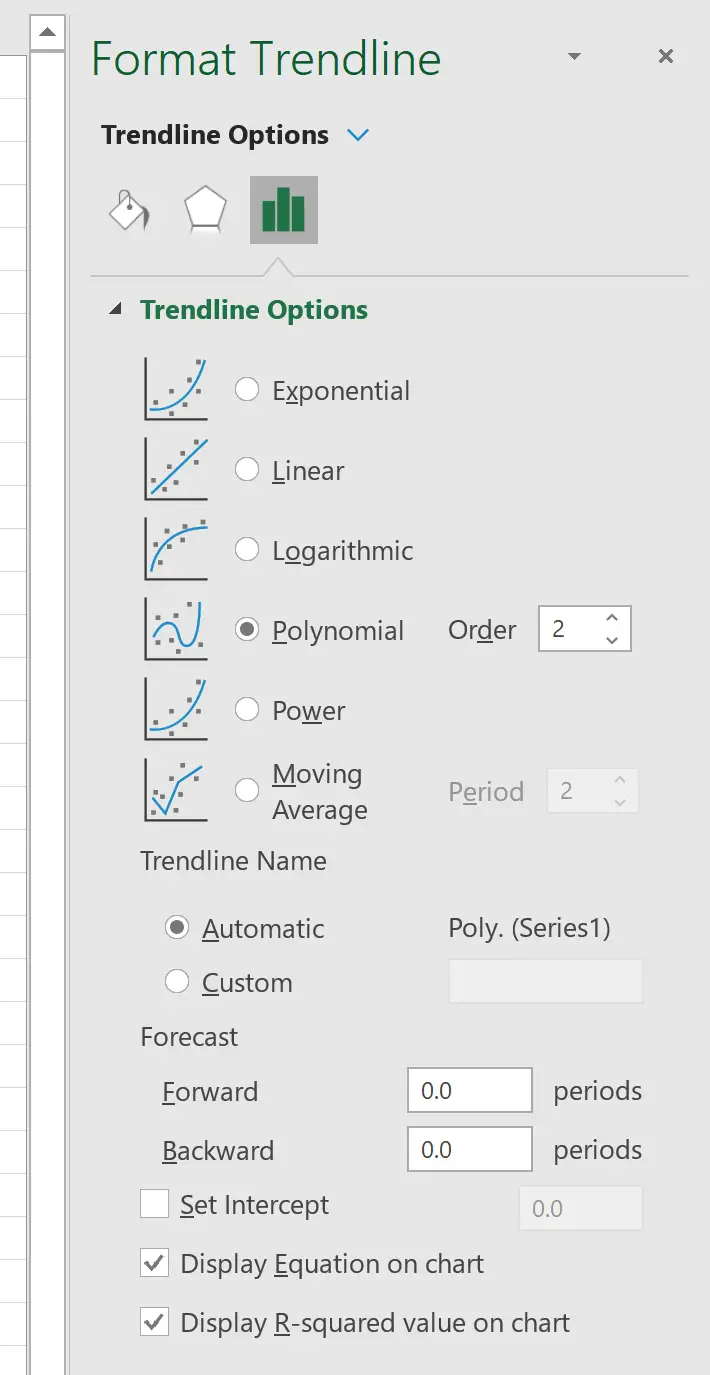
右側に表示されるウィンドウで、 [多項式]の横にあるボタンをクリックします。次に、 [チャートに式を表示]と[チャートに R 二乗値を表示] の横のボックスをオンにします。
これにより、点群上に次の曲線が生成されます。
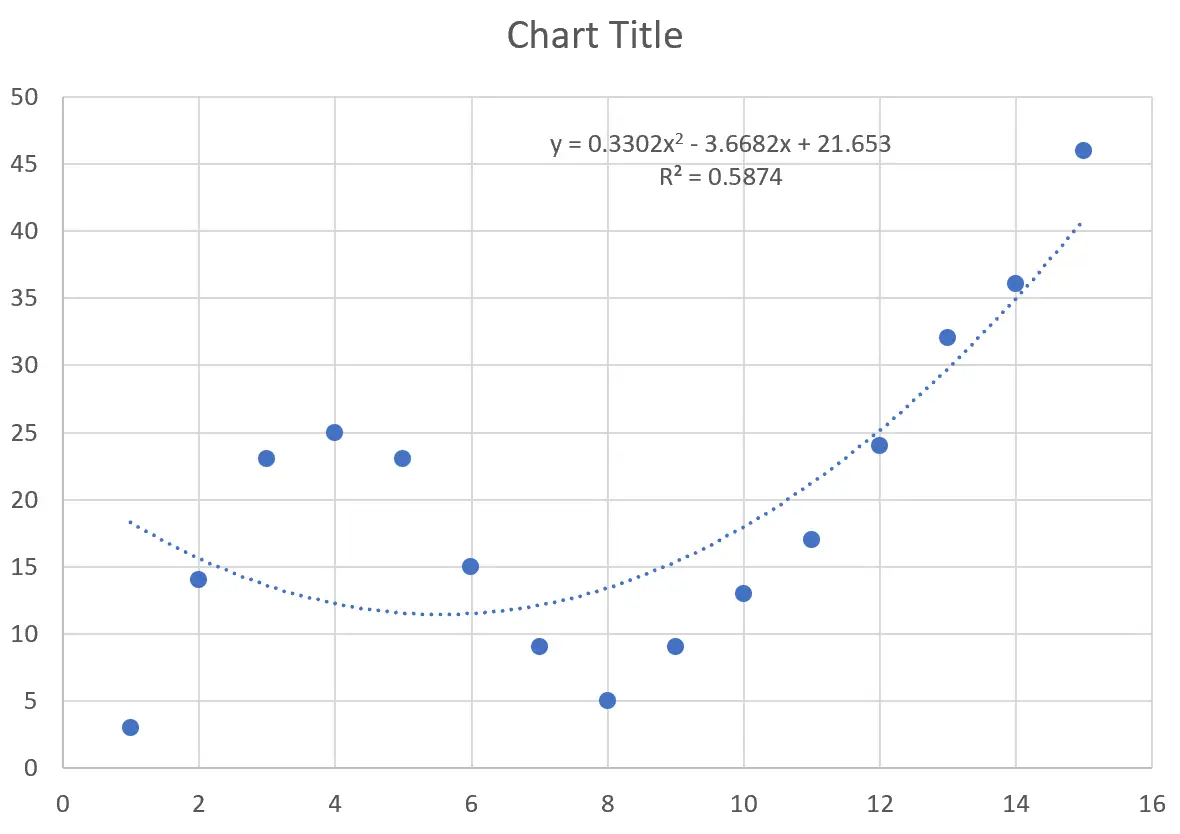
曲線の方程式は次のとおりです。
y = 0.3302x 2 – 3.6682x + 21.653
R 二乗は、予測変数によって説明できる応答変数の変動のパーセンテージを示します。この特定の曲線の R 二乗は0.5874です。
ステップ 4: 最適なトレンドラインを選択する
また、使用している多項式の次数を増やして、より柔軟な曲線がデータセットによりよく適合するかどうかを確認することもできます。
たとえば、多項式の次数を 4 に設定することを選択できます。
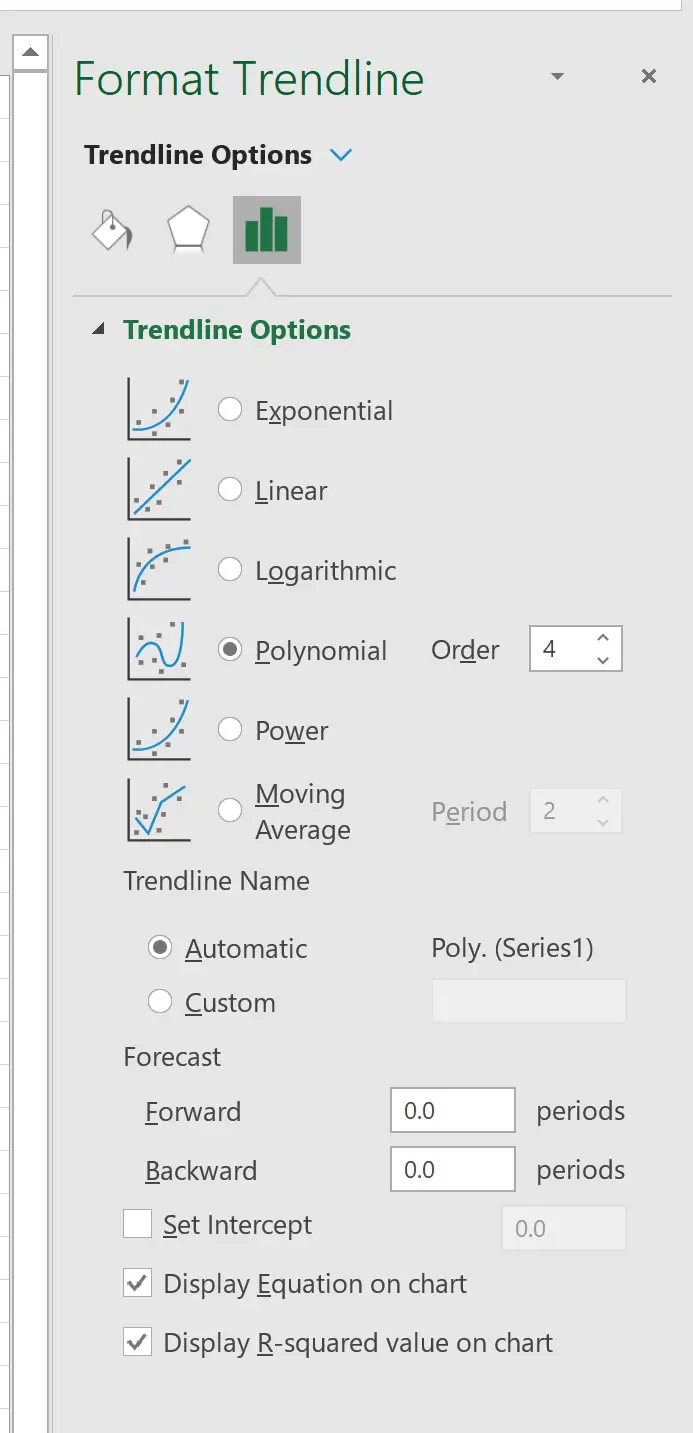
これにより、次の曲線が得られます。
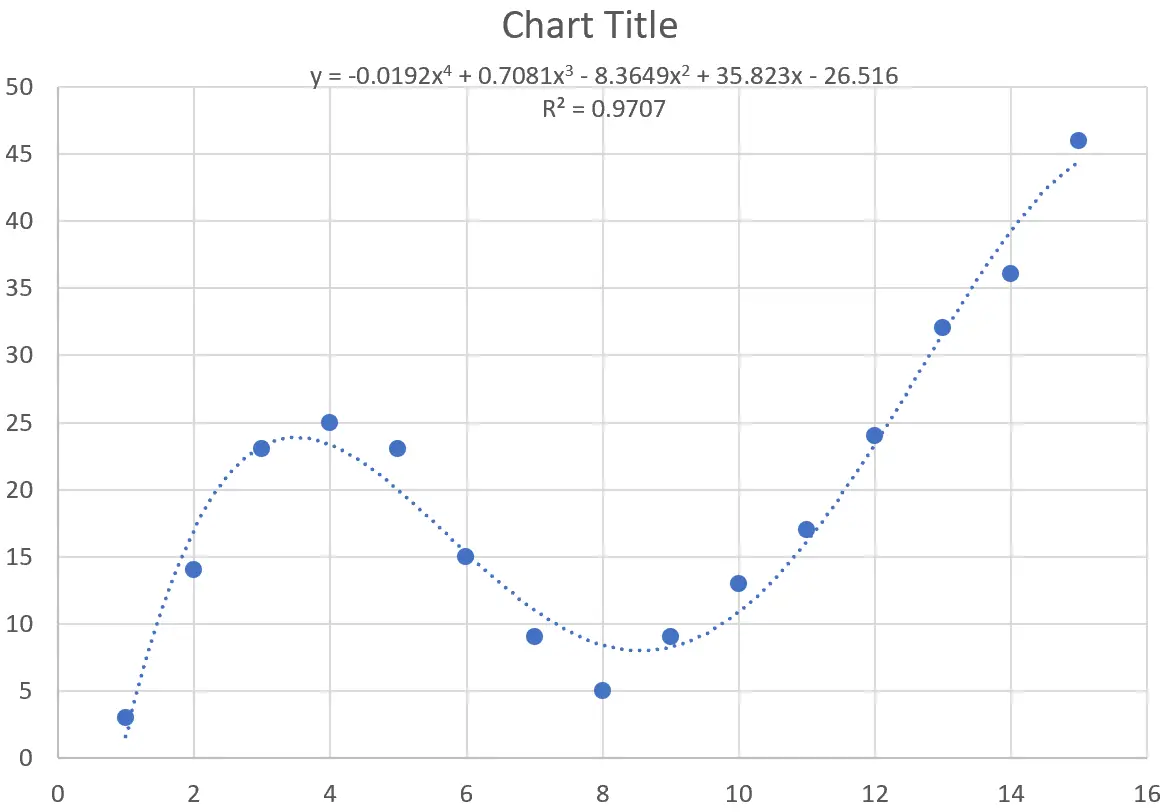
曲線の方程式は次のとおりです。
y = -0.0192x 4 + 0.7081x 3 – 8.3649x 2 + 35.823x – 26.516
この特定の曲線の R 二乗は0.9707です。
この R 二乗値は前の曲線の R 二乗値よりもかなり高く、データ セットとより厳密に一致していることを示しています。
この曲線方程式を使用して、予測変数に基づいて応答変数の値を予測することもできます。たとえば、 x = 4 の場合、 y = 23.34と予測します。
y = -0.0192(4) 4 + 0.7081(4) 3 – 8.3649(4) 2 + 35.823(4) – 26.516 = 23.34
このページでは、その他の Excel チュートリアルを見つけることができます。