Excelで回帰の標準誤差を計算する方法

線形回帰モデルを当てはめます。モデルは次の形式になります。

Y = β ₀ + β ₁ X + … + β _i

ここで、ϵ は X から独立した誤差項です。

X をどのように使用して Y の値を予測できるかに関係なく、モデルには常にランダムな誤差が存在します。

このランダム誤差の分散を測定する 1 つの方法は、回帰モデルの標準誤差を使用することです。これは、残差 ϵ の標準偏差を測定する方法です。

このチュートリアルでは、Excel で回帰モデルの標準誤差を計算する方法を段階的に説明します。

ステップ 1: データを作成する

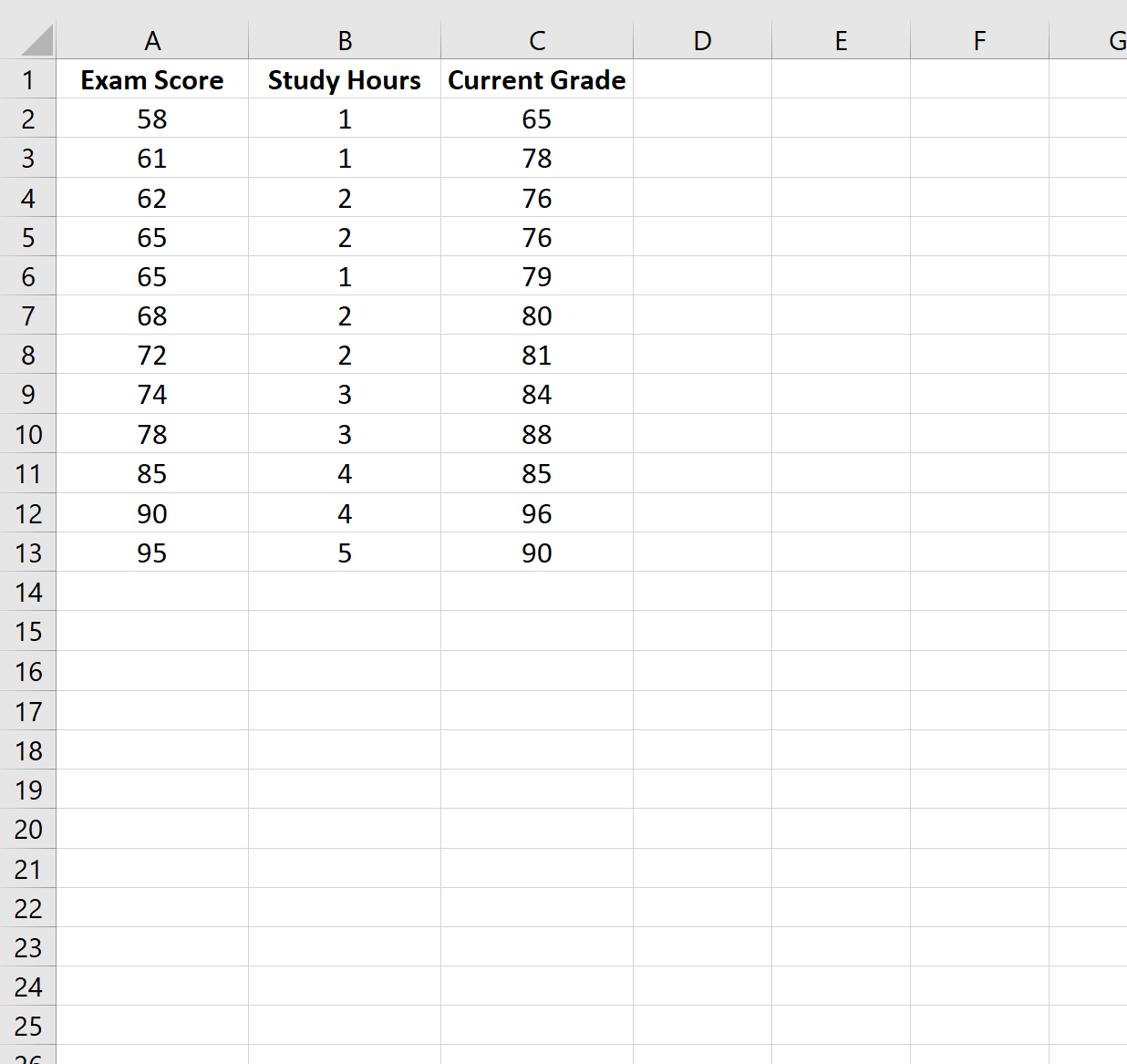
この例では、12 人の異なる生徒に対して次の変数を含むデータセットを作成します。

• 試験の結果
• 勉強に費やした時間
• 現在のクラス

ステップ 2: 回帰モデルを当てはめる

次に、試験のスコアを応答変数として、学習時間と現在の成績を予測変数として使用して、重線形回帰モデルを近似します。

これを行うには、上部のリボンに沿って[データ]タブをクリックし、 [データ分析] をクリックします。

このオプションが使用できない場合は、まずData Analysis ToolPak をロードする必要があります。

表示されるウィンドウで、 「回帰」を選択します。表示される新しいウィンドウで、次の情報を入力します。

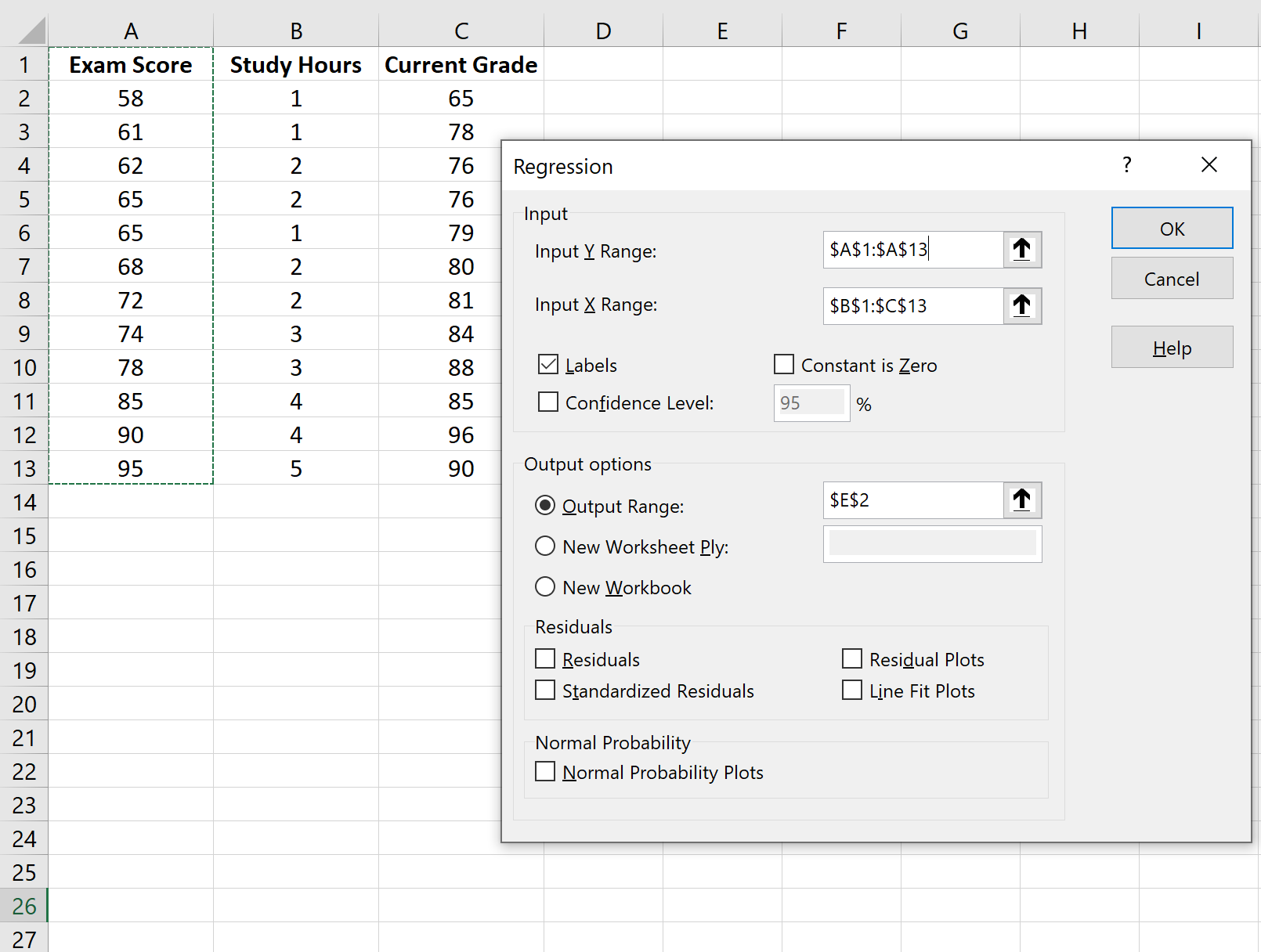
[OK]をクリックすると、回帰モデルの出力が表示されます。

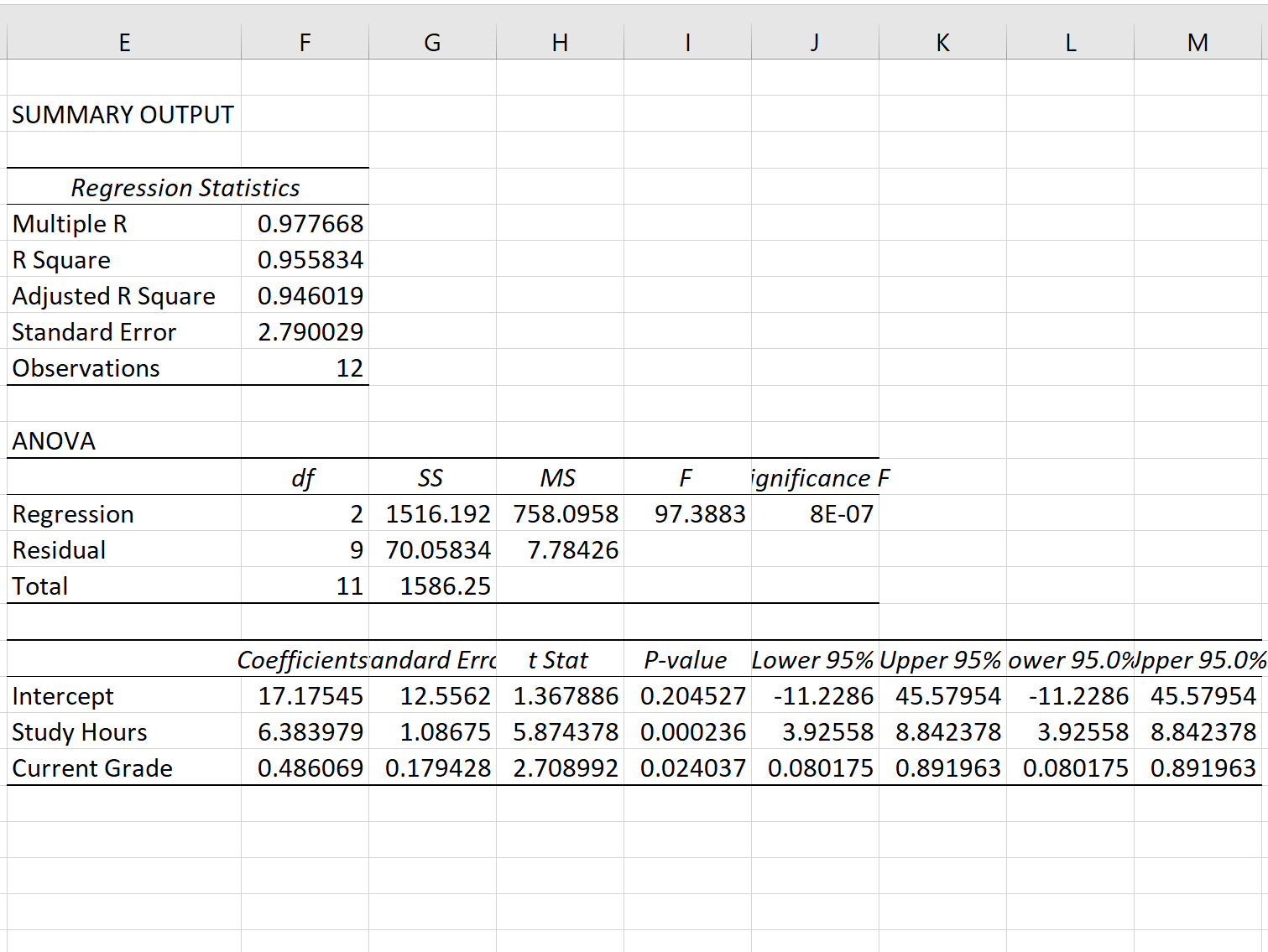
ステップ 3: 回帰標準誤差を解釈する

回帰モデルの標準誤差は、標準誤差の隣の数字です。

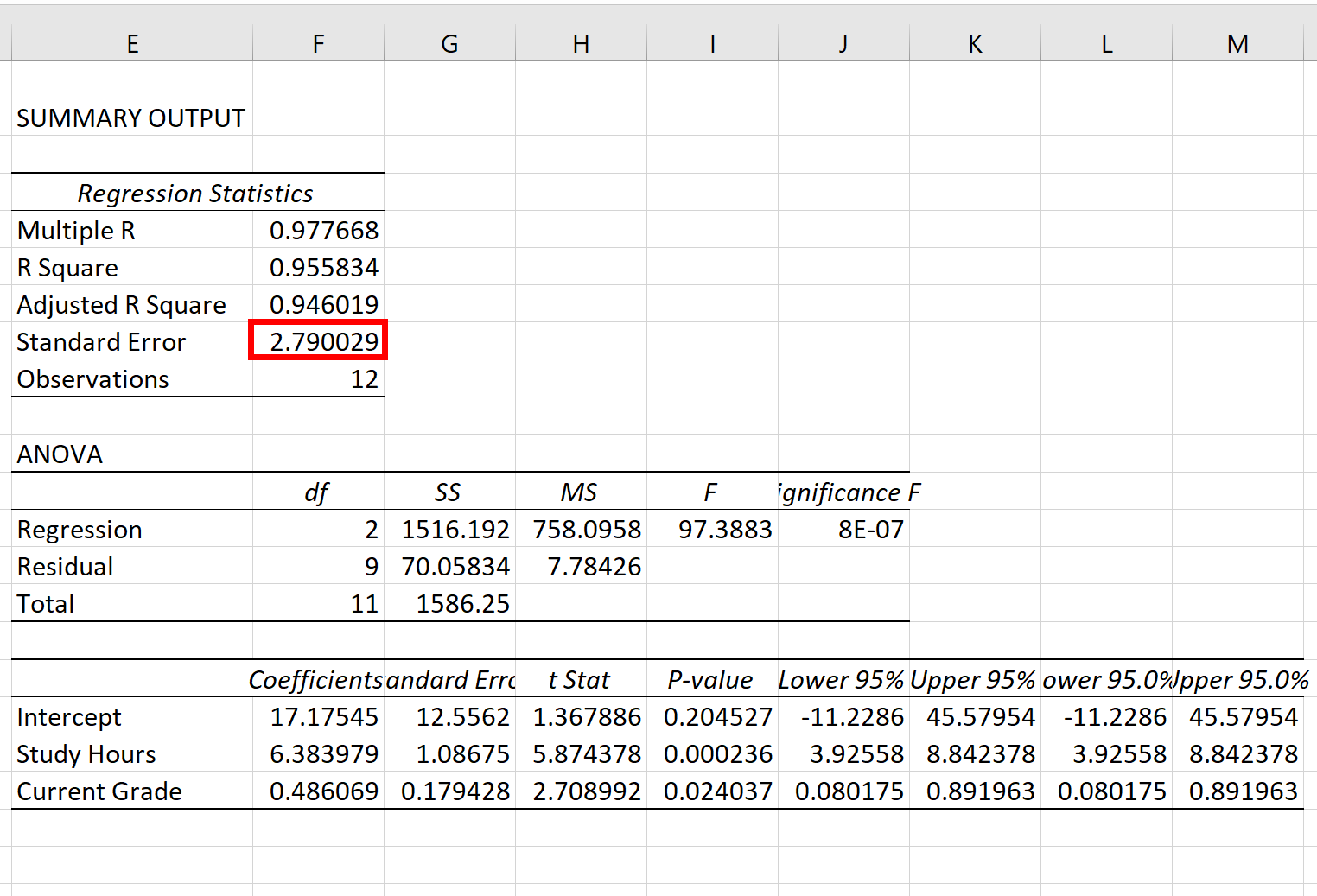
この特定の回帰モデルの標準誤差は2.790029であることがわかります。

この数値は、実際の検査結果とモデルによって予測された検査結果の間の平均距離を表します。

一部の試験結果は予測スコアから 2.79 単位以上離れていますが、他の結果は予測スコアに近いものもあります。ただし、実際の試験結果と予測結果の間の距離は平均して2.790029です。

また、回帰の標準誤差が小さいほど、回帰モデルがデータセットによりよく適合していることを示していることにも注意してください。

したがって、新しい回帰モデルをデータセットに当てはめて、たとえば4.53の標準誤差が得られた場合、この新しいモデルは試験の得点を予測する効果が以前のモデルよりも低くなります。

追加リソース

回帰モデルの精度を測定するもう 1 つの一般的な方法は、R 二乗を使用することです。回帰の標準誤差を使用して精度と R2 乗を測定する利点については、この記事をご覧ください。