Excel で多項式近似曲線を追加する方法 (例付き)
多項式傾向線は、 2 つの変数間の非線形関係を捉えることができる傾向線の一種です。
次の段階的な例は、Excel でデータ セットの多項式傾向線を計算して解釈する方法を示しています。
ステップ 1: データを作成する
まず、Excel で次のデータセットを作成しましょう。
ステップ 2: 散布図を挿入する
次に、散布図を挿入して、データセット内の 2 つの変数間の関係を視覚化します。
これを行うには、セル範囲A2:B15を強調表示し、上部のリボンに沿って[挿入]タブをクリックし、 [グラフ]グループの[散布図]アイコンをクリックします。
次の点群が自動的に表示されます。
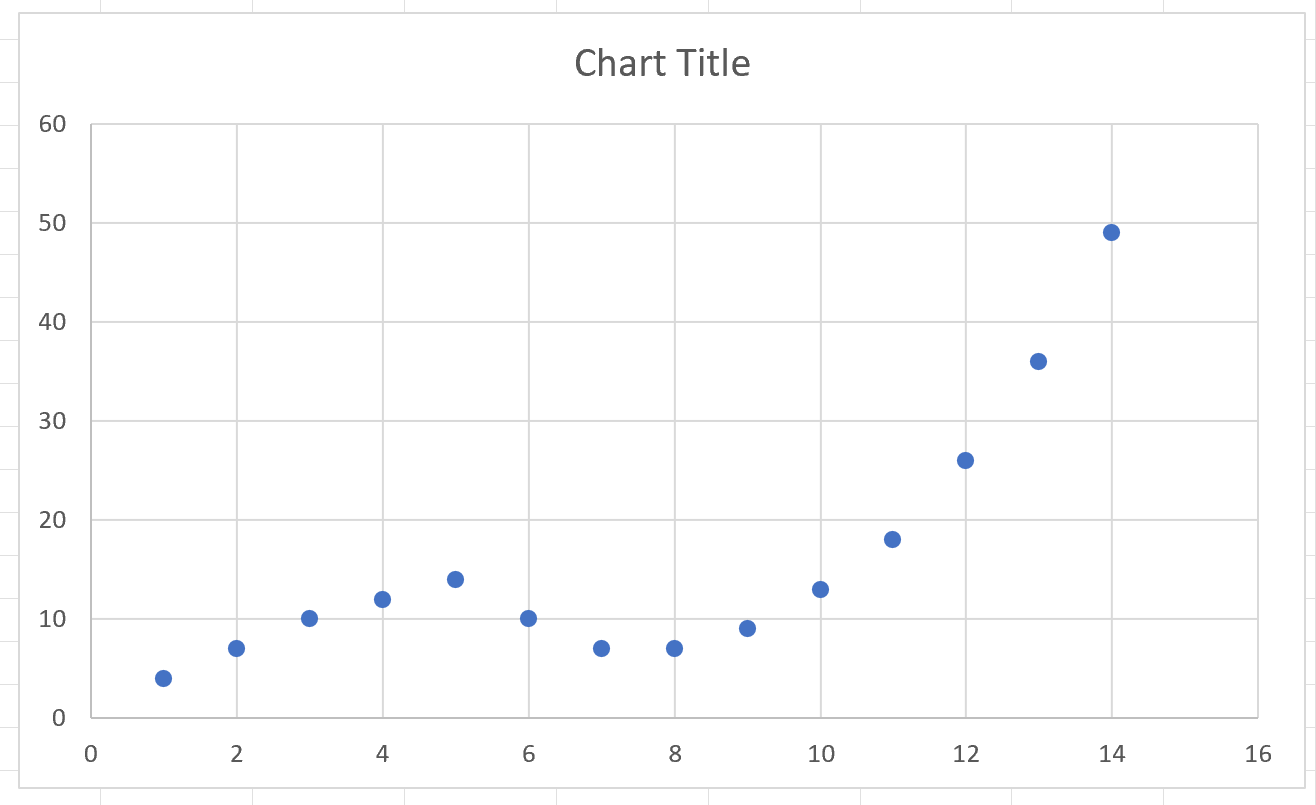
グラフを見るだけで、データセット内の 2 つの変数に線形関係がないことがわかります。
したがって、多項式傾向線は、2 つの変数間の関係をより適切に捉える可能性があります。
ステップ 3: 多項式近似曲線を挿入する
多項式傾向線をプロットに挿入するには、チャート上の任意の場所をクリックしてアクティブにします。
次に、右上隅にある小さな緑色のプラス記号をクリックし、 [トレンドライン]の横にあるドロップダウン矢印をクリックして、 [その他のオプション]をクリックします。

表示される[トレンドラインの書式設定]パネルで、 [トレンドライン オプション]の下の[多項式]をクリックし、 [次数] に3 を入力します。
最後に、 「グラフに方程式を表示」の横にあるボックスをチェックします。
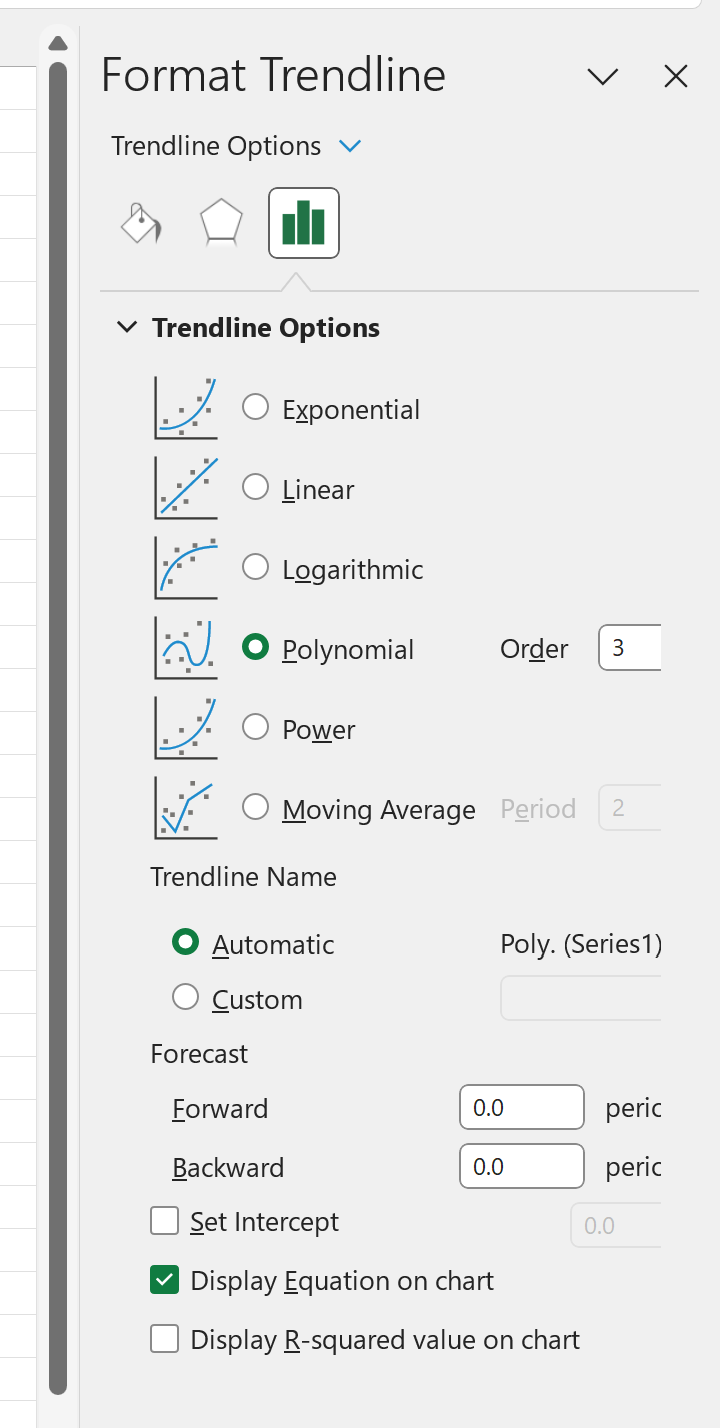
次数3の多項式傾向線が散布図に表示されます。
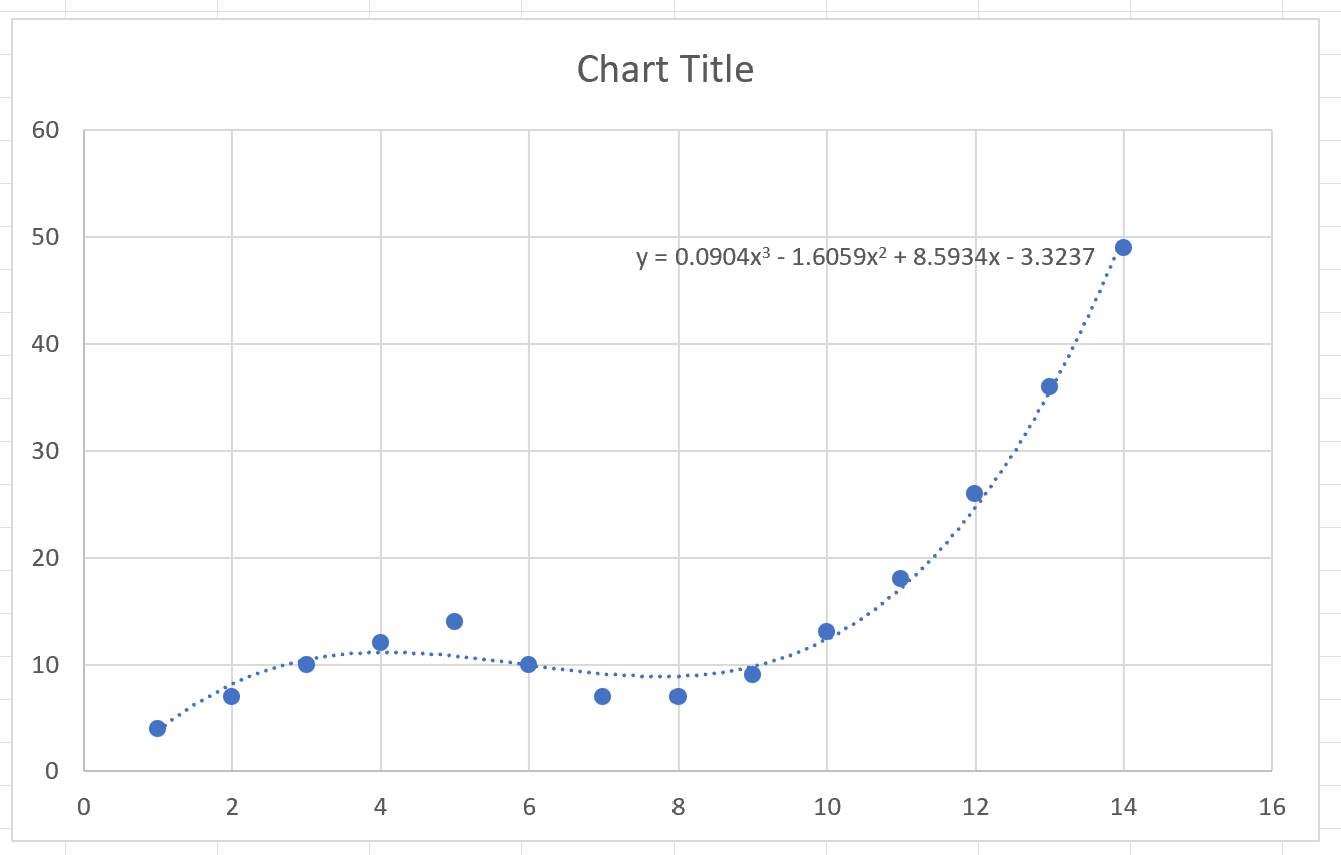
近似曲線は、データセット内の 2 つの変数間の関係を非常によく捉えていることがわかります。
チャート上には多項式傾向線の方程式も表示されます。
y = 0.0904x 3 – 1.6059x 2 + 8.5934x – 3.3237
近似曲線方程式を使用して、x の値を考慮して y の期待値を計算できます。
たとえば、x = 4 と仮定します。y の期待値は次のようになります。
y = 0.0904(4) 3 – 1.6059(4) 2 + 8.5934(4) – 3.3237 = 11.1411
x が 4 の場合、y の期待値は11.1411です。
追加リソース
次のチュートリアルでは、Excel で他の一般的なタスクを実行する方法について説明します。