Excelでvifを計算する方法
回帰分析における多重共線性は、2 つ以上の説明変数が相互に高度に相関しており、回帰モデル内で固有または独立した情報を提供しない場合に発生します。変数間の相関度が十分に高い場合、回帰モデルのフィッティングと解釈の際に問題が発生する可能性があります。
幸いなことに、分散膨張係数 (VIF)と呼ばれる指標を使用して多重共線性を検出することができます。この指標は、回帰モデル内の説明変数間の相関と相関の強さを測定します。
このチュートリアルでは、Excel で VIF を計算する方法を説明します。
例: Excel で VIF を計算する
この例では、10 人のバスケットボール選手の属性を記述する次のデータセットを使用して重回帰を実行します。評価を応答変数として、ポイント、アシスト、リバウンドを説明変数として使用して回帰モデルを当てはめます。次に、各説明変数の VIF 値を特定します。
ステップ 1: 重回帰を実行します。
上部のリボンで、[データ] タブに移動し、[データ分析] をクリックします。このオプションが表示されない場合は、まず無料の Analysis ToolPak ソフトウェアをインストールする必要があります。

「データ分析」をクリックすると、新しいウィンドウが表示されます。 「回帰」を選択し、「OK」をクリックします。

応答変数と説明変数に必要なテーブルを入力し、「OK」をクリックします。
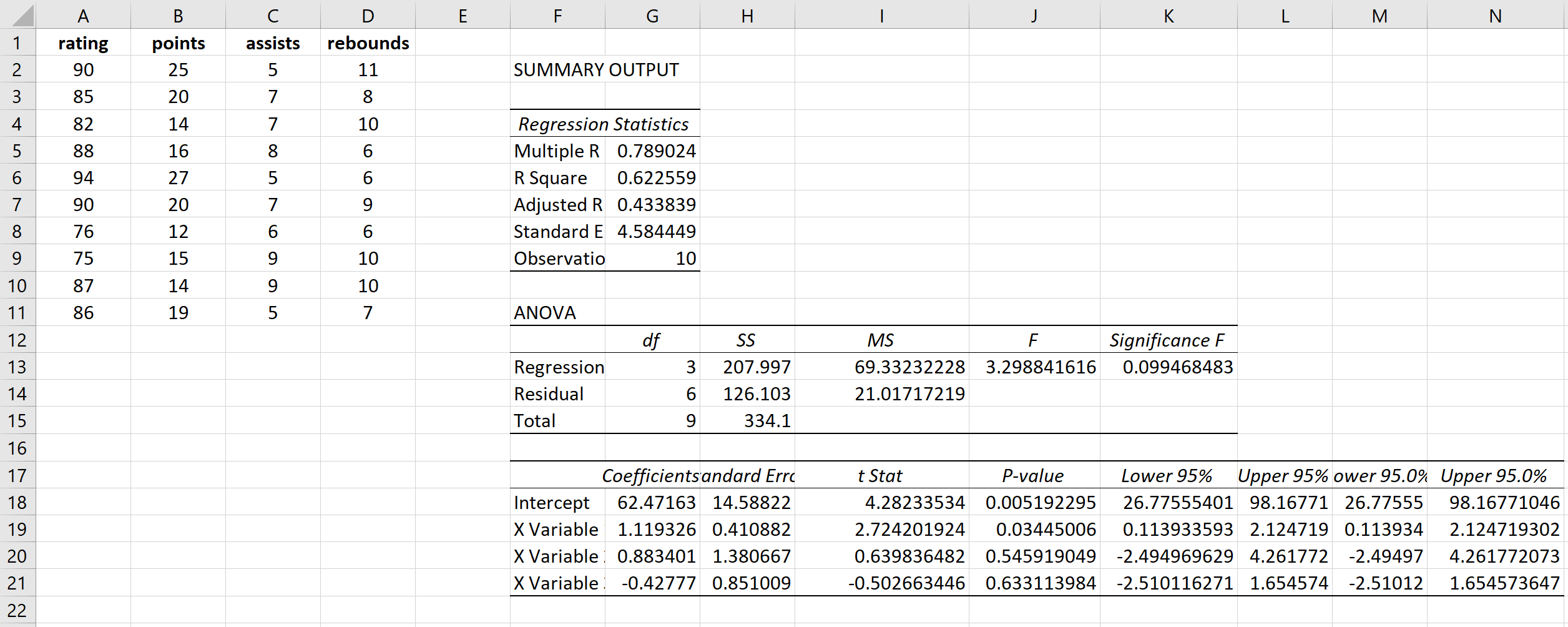
これにより、次の結果が生成されます。
ステップ 2: 各説明変数の VIF を計算します。
次に、1 つの説明変数を応答変数として使用し、他の 2 つを説明変数として使用して個別の回帰を実行することにより、3 つの説明変数それぞれの VIF を計算できます。
たとえば、ポイントを応答変数として、アシストとリバウンドを説明変数として使用して重線形回帰を実行することにより、ポイント変数の VIF を計算できます。
これにより、次の結果が生成されます。

ポイントの VIF は、1 / (1 – R Square) = 1 / (1 – .433099) = 1.76として計算されます。
次に、他の 2 つの変数、アシストとリバウンドに対してこのプロセスを繰り返すことができます。
3 つの説明変数の VIF は次のとおりであることがわかります。
ポイント: 1.76
アシスト: 1.96
リバウンド: 1.18
VIF 値の解釈方法
VIF 値は 1 から始まり、上限はありません。 VIF を解釈するための一般的なルールは次のとおりです。
- 値 1 は、モデル内の特定の説明変数と他の説明変数の間に相関関係がないことを示します。
- 1 ~ 5 の値は、特定の説明変数とモデル内の他の説明変数の間に中程度の相関関係があることを示しますが、多くの場合、特別な注意を必要とするほど深刻ではありません。
- 5 より大きい値は、モデル内の特定の説明変数と他の説明変数の間に重大な相関関係がある可能性があることを示します。この場合、回帰結果の係数推定値と p 値は信頼できない可能性があります。
回帰モデルの説明変数の VIF 値はそれぞれ 1 に近いため、この例では多重共線性は問題になりません。