Excel で不等分散を使用した t 検定を実行する方法
2 標本 t 検定は、 2 つの母集団の平均が等しいかどうかを判断するために使用されます。
使用できる 2 つの t 検定の例には 2 つのバージョンがあります。
- 等分散による t 検定
- 不等分散による t 検定
2 つのサンプルの分散が等しくない場合は、不等分散による t 検定を使用します。
2 つのサンプル間の分散が等しいかどうかを判断する最も簡単な方法は、分散の経験則を使用することです。
一般に、最大分散と最小分散の比が 4 未満の場合、分散はほぼ等しいと想定できます。
それ以外の場合、比率が 4 以上の場合、分散は等しくないものとみなされます。
次のステップバイステップの例は、Excel で不等分散を使用した 2 標本 t 検定を実行する方法を示しています。
ステップ 1: データを入力する
2 つの異なる学習方法が、特定の大学の学生間で異なる試験平均点につながるかどうかを判断したいとします。
20 人の学生からなるサンプルをランダムに選択し、各学習方法を使用して試験結果を記録します。
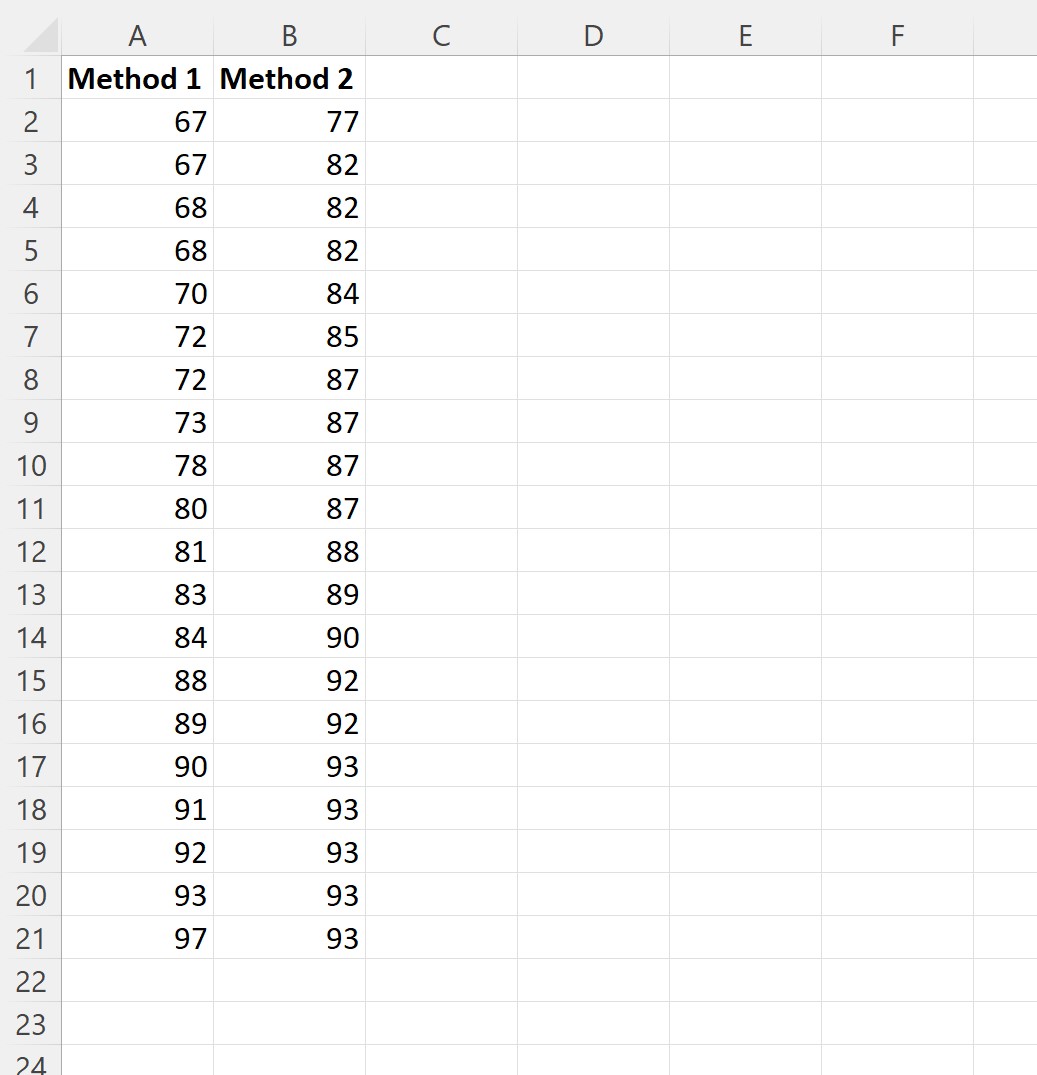
ステップ 2: 等しい分散または不等な分散を決定する
次に、標本分散の比率を計算できます。
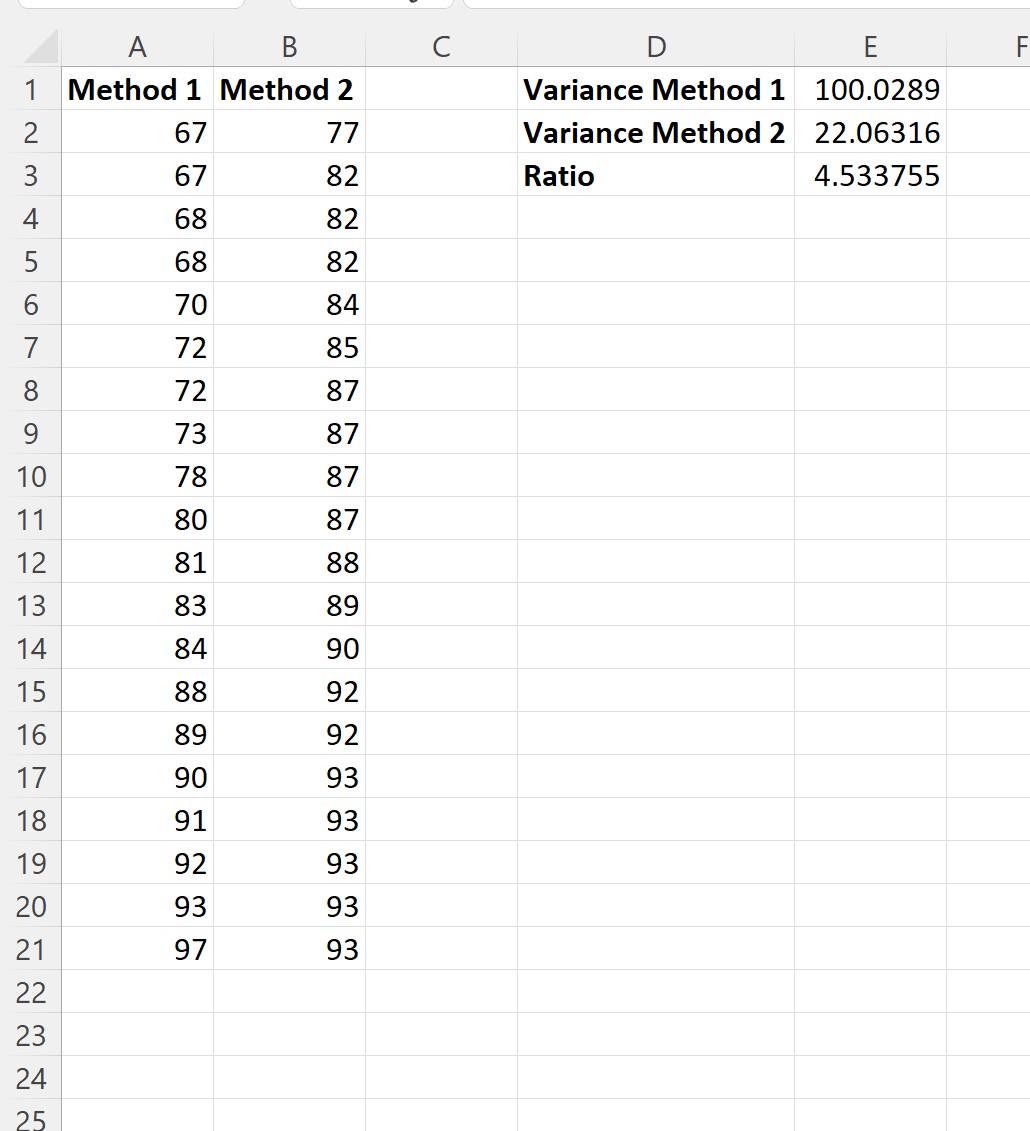
各セルに入力した数式は次のとおりです。
- セル E1: =VAR.S(A2:A21)
- セル E2: =VAR.S(B2:B21)
- セル E3: =E1/E2
最大の標本分散と最小の標本分散の比は4.533755であることがわかります。
この値が 4 以上である場合、2 つのサンプル間の分散は等しくないと仮定します。
ステップ 3: 不等分散を使用して 2 標本 t 検定を実行する
次に、不等分散を使用した 2 サンプルの t 検定を実行して、2 つのサンプル間の試験の平均スコアが等しいかどうかを判断できます。
これを行うには、上部のリボンの[データ]タブをクリックし、 [分析]グループの[データ分析]ボタンをクリックします。

このボタンが表示されない場合は、まずExcel に無料のデータ分析ツールパックをインストールする必要があります。
表示される新しいウィンドウで、 [T 検定: 不等分散を仮定した 2 標本]をクリックし、 [OK ] をクリックします。
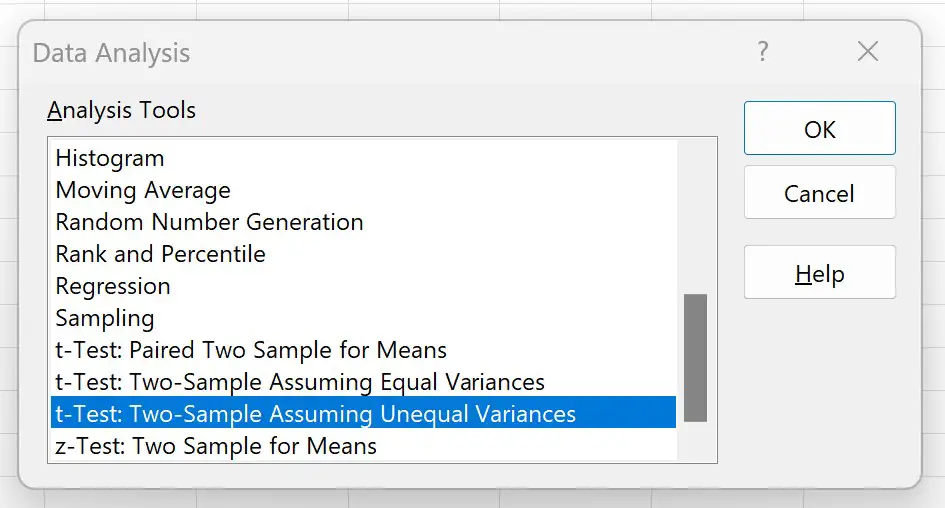
表示される新しいウィンドウに次の情報を入力し、 [OK]をクリックします。
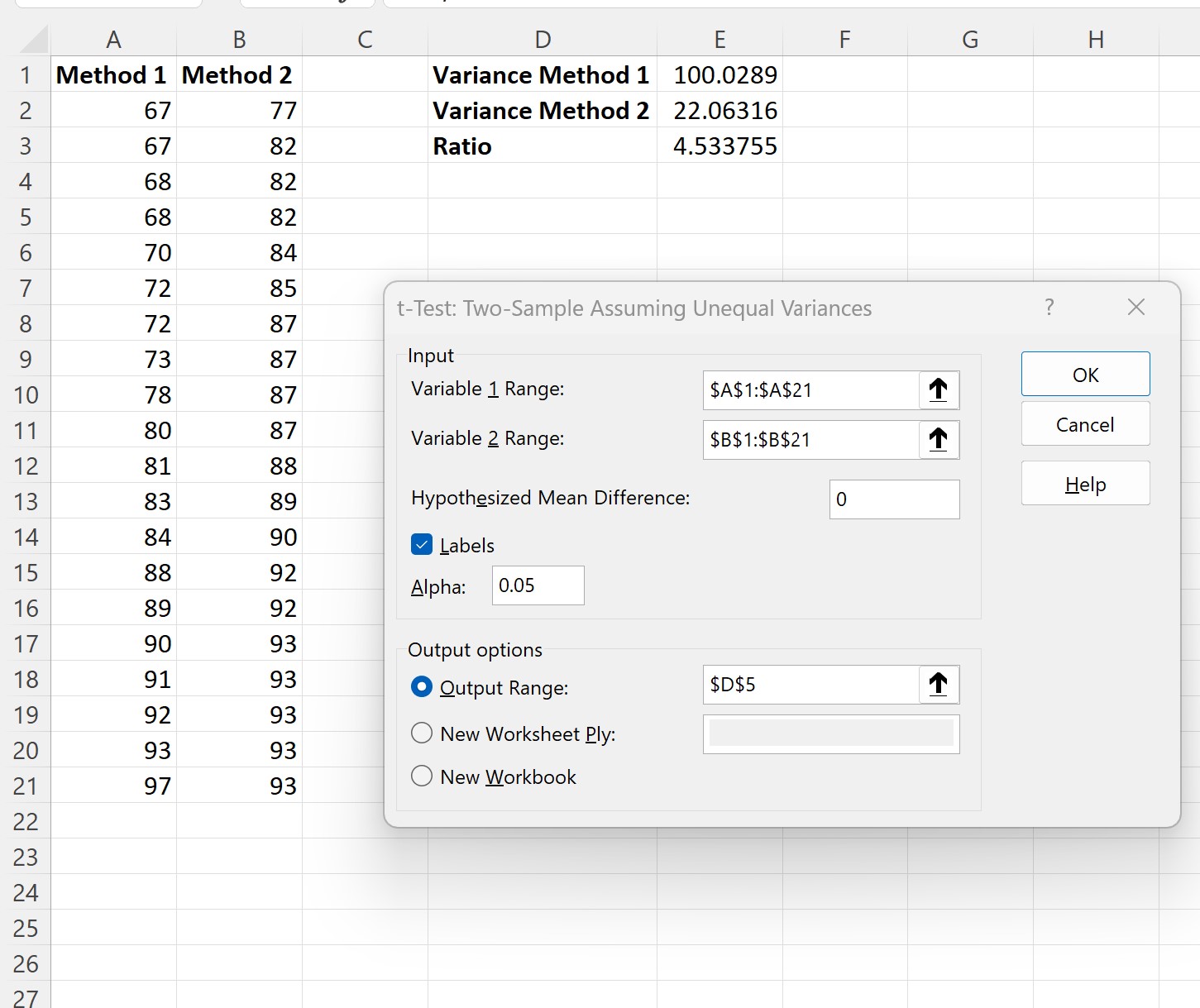
[OK]をクリックすると、2 つの t 検定の例の結果が表示されます。
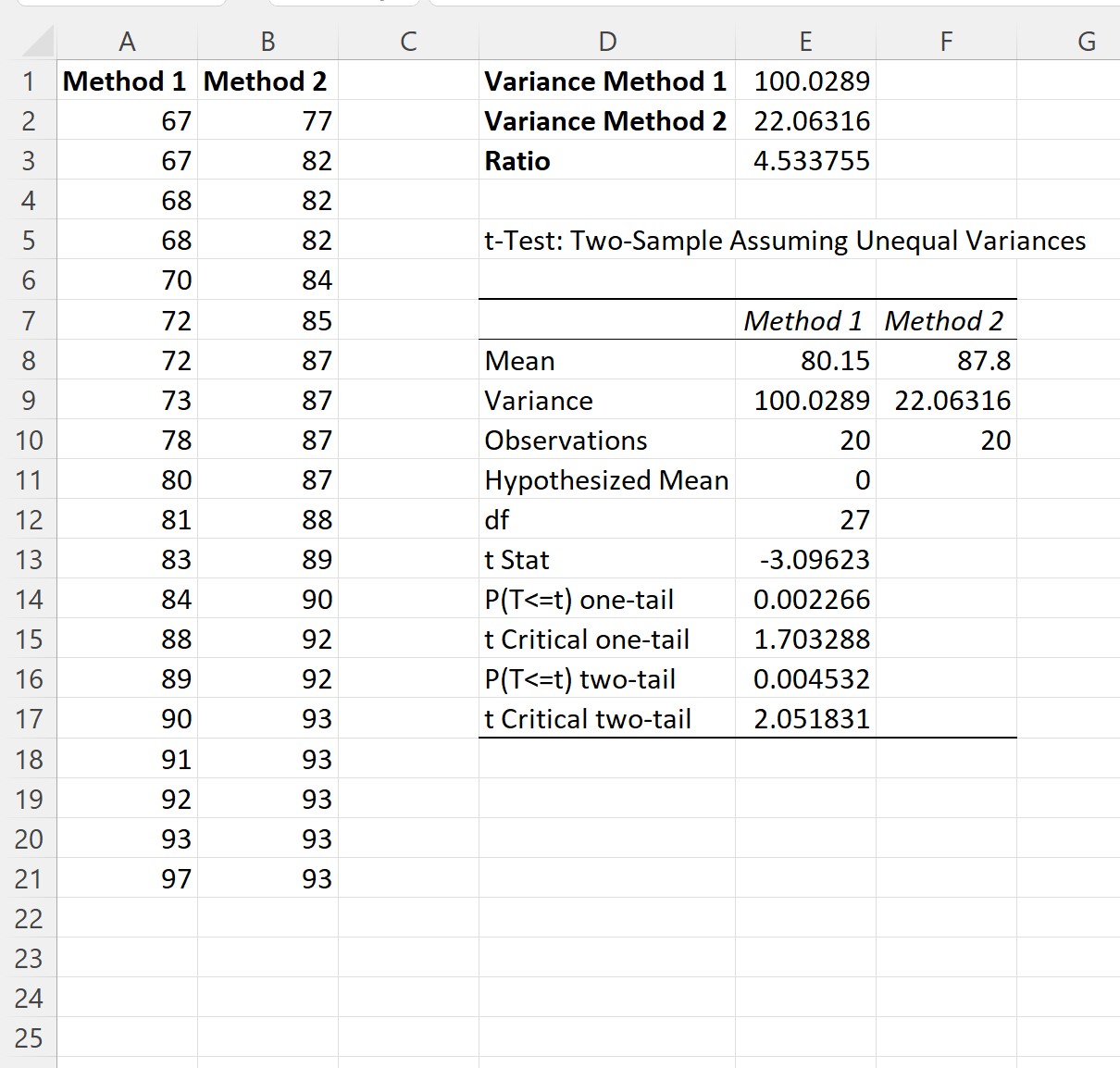
ステップ 4: 結果を解釈する
結果から次のことがわかります。
- 方法 1 の試験の平均スコアは80.15でした。
- 方法 2 の試験の平均スコアは87.8でした。
- t 検定統計量は-3.09623でした。
- 対応する両側 p 値は0.004532でした。
この p 値は 0.05 未満であるため、2 つの学習方法の間には試験の平均点に統計的に有意な差があると結論付けることができます。
追加リソース
次のチュートリアルでは、Excel で他の一般的なタスクを実行する方法について説明します。
Excel で 1 サンプルの t 検定を実行する方法
Excel で対応のあるサンプルの t 検定を実行する方法
Excel で 1 つのサンプルと 2 つのサンプルの Z テストを実行する方法