Excel で最適な線を作成する方法
統計学において、最良適合線とは、予測変数と応答変数の間の関係を最もよく「適合」する線、またはその関係を説明する線のことです。
次のステップバイステップの例は、Excel で最適な線を作成する方法を示しています。
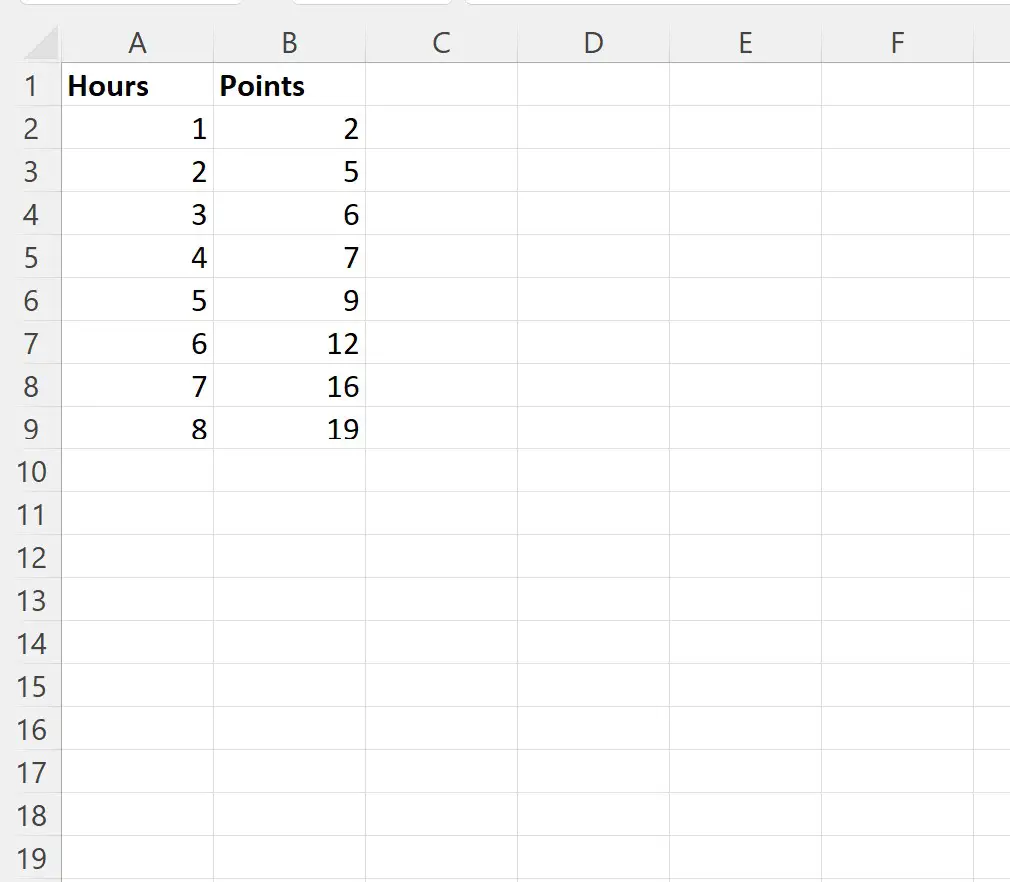
ステップ 1: データを入力する
まず、8 人の異なるバスケットボール選手がトレーニングに費やした時間数と合計得点を示す次のデータセットを入力してみましょう。
ステップ 2: 散布図を作成する
次に、散布図を作成して 2 つの変数間の関係を視覚化しましょう。
これを行うには、範囲A2:B9内のセルを強調表示し、上部のリボンに沿って[挿入]タブをクリックし、 [グラフ]グループで[散布]というラベルの付いたオプションをクリックします。
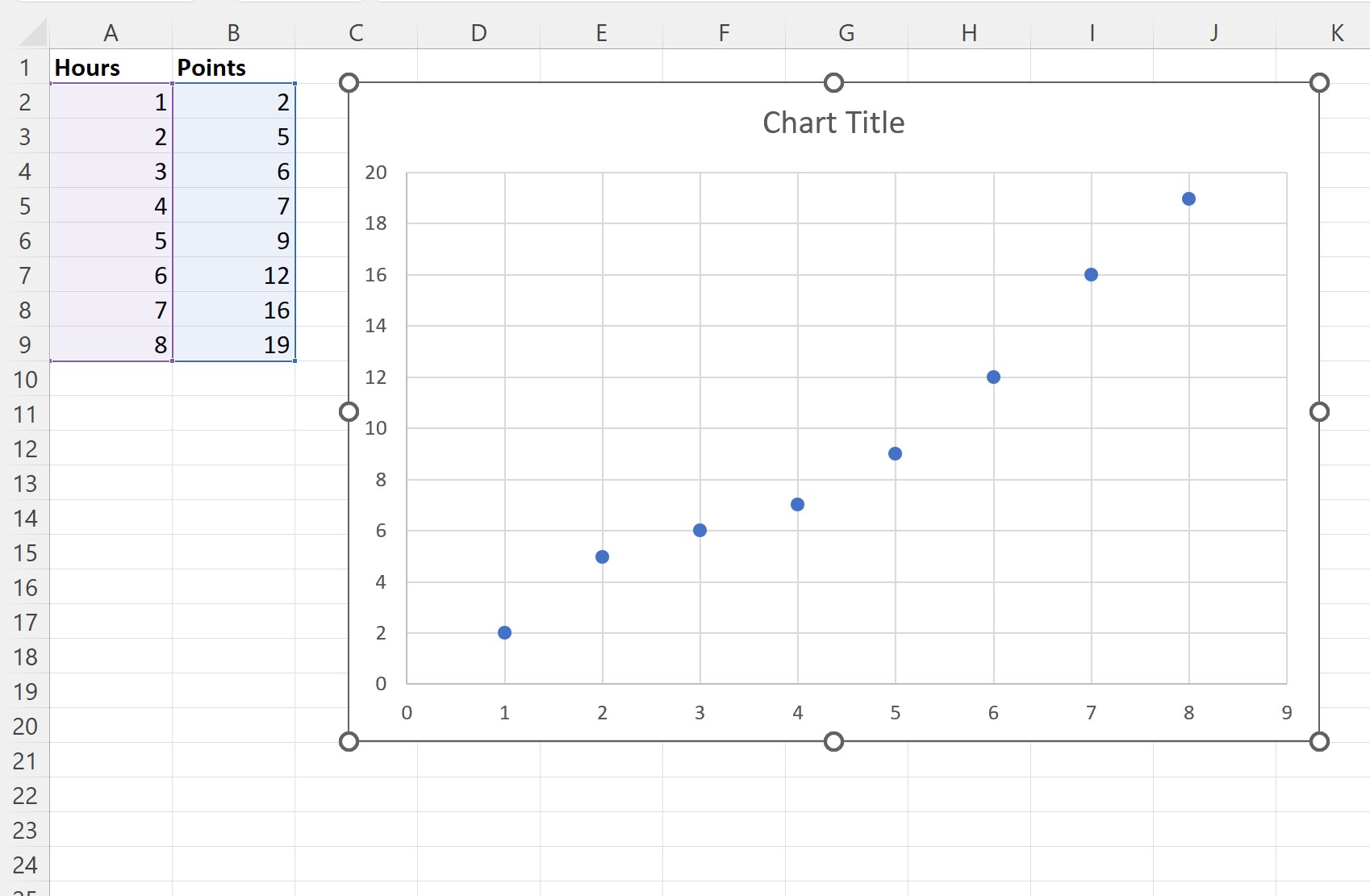
次の点群が自動的に作成されます。
ステップ 3: 最適な線を追加する
散布図に最適な線を追加するには、グラフ上の任意の場所をクリックし、グラフの右上隅に表示される緑色のプラス (+) 記号をクリックします。
次に、 [トレンドライン]の横にある矢印をクリックし、 [その他のオプション]をクリックします。
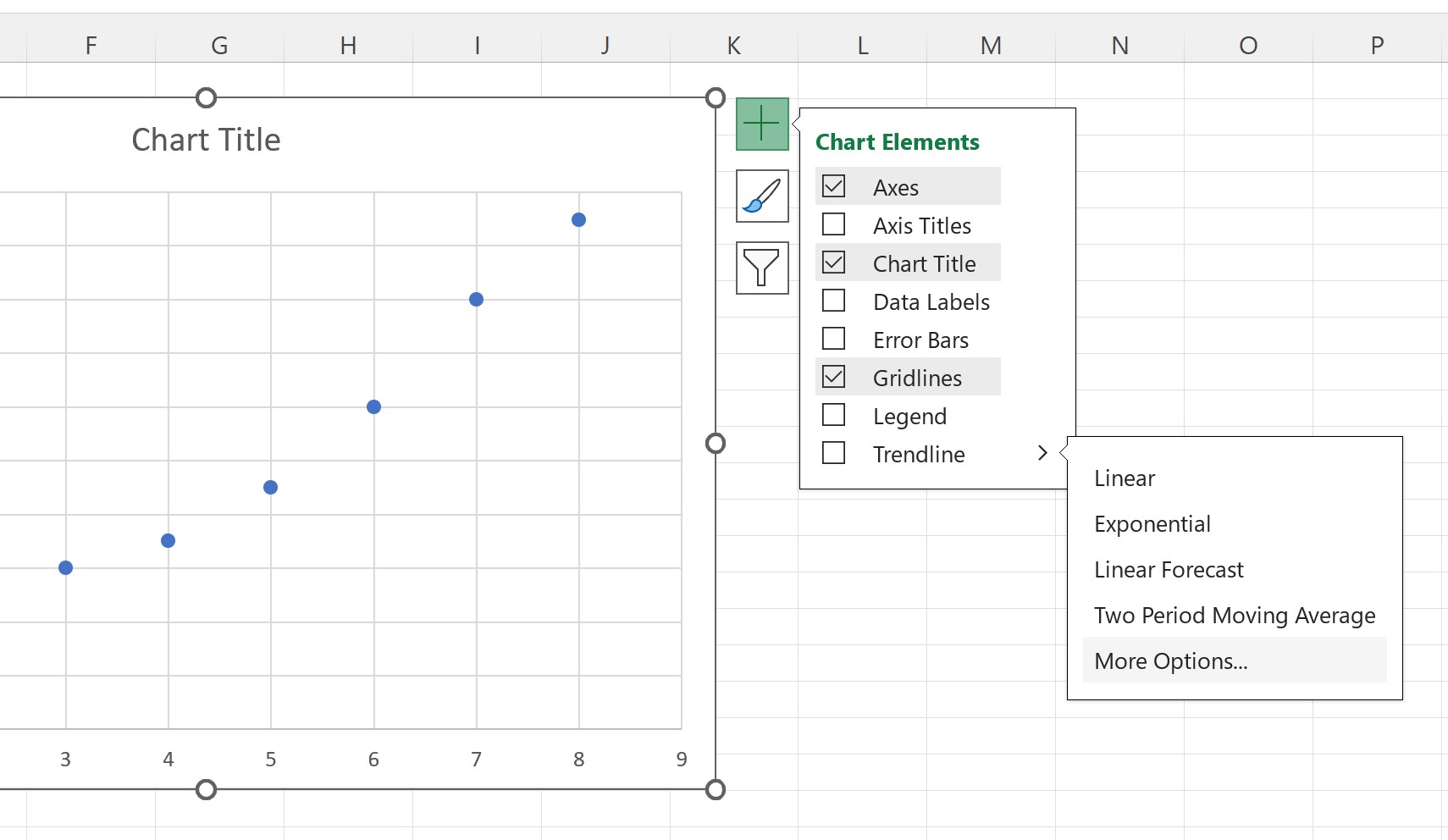
表示される [トレンドラインの形式] パネルで、 [トレンドラインとして線形]オプションの横にあるボタンをクリックし、 [チャートに方程式を表示]の横にあるボックスをオンにします。
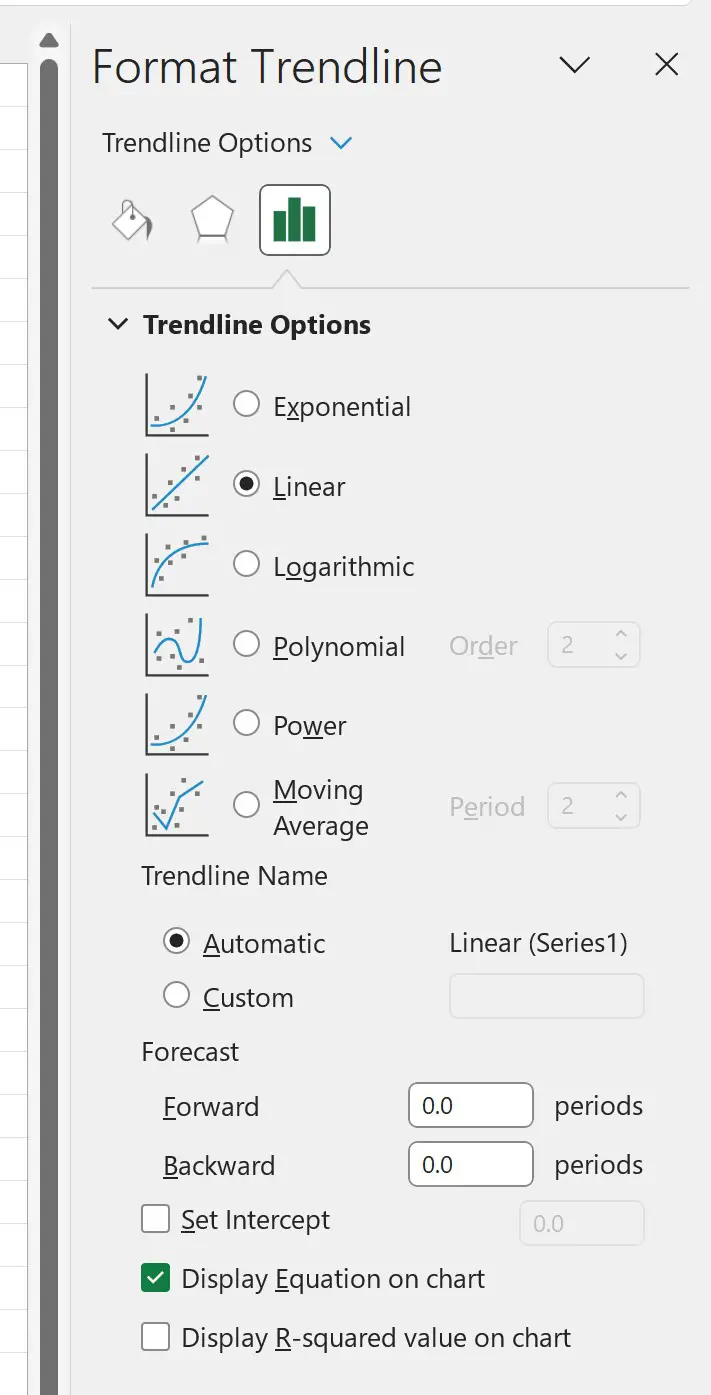
最適な直線とその直線の方程式がグラフに表示されます。
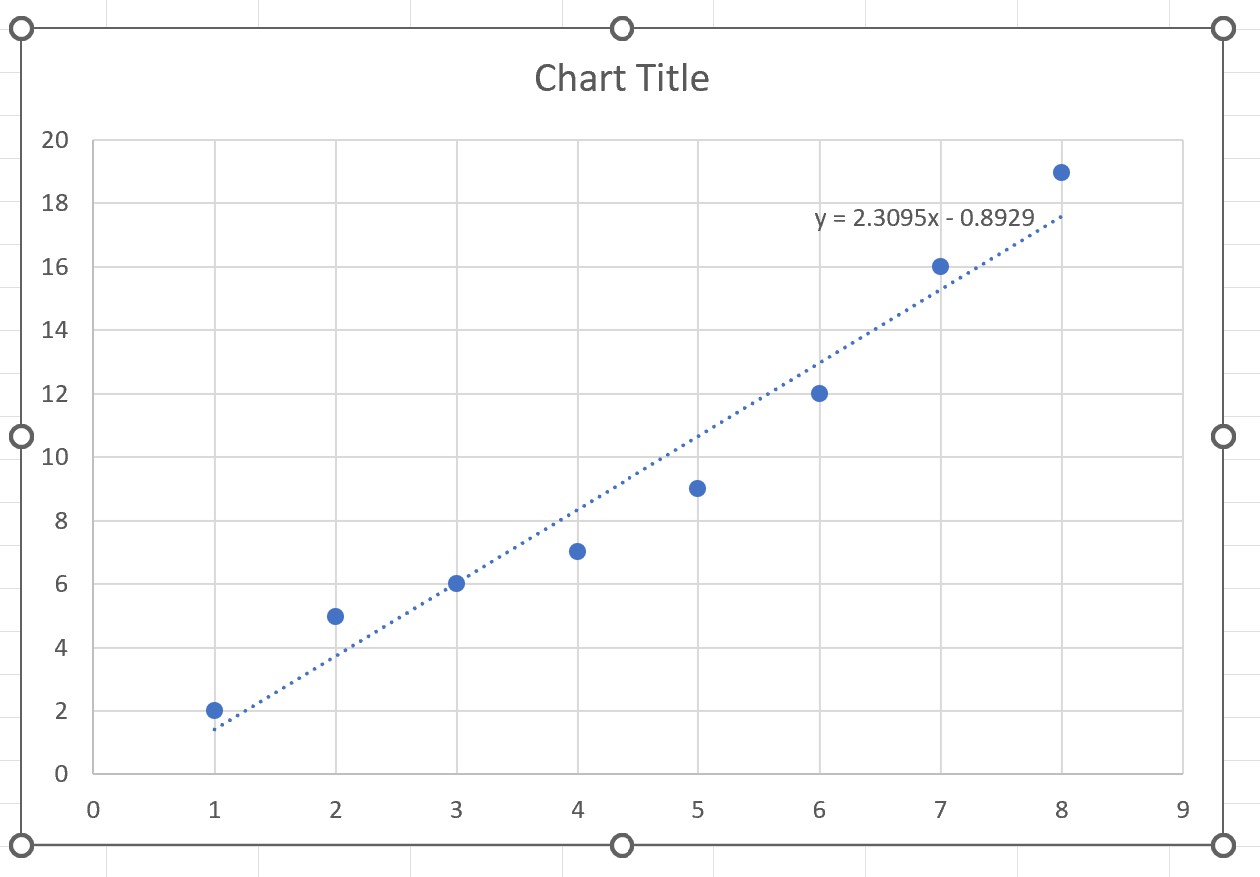
ステップ 4: 最適な線を解釈する
グラフから、最適な直線には次の方程式があることがわかります。
y = 2.3095x – 0.8929
この方程式を解釈する方法は次のとおりです。
- 練習にさらに 1 時間費やすごとに、平均得点は2.3095ずつ増加します。
- 練習時間が 0 時間のプレーヤーの場合、平均得点は-0.8929になるはずです。
回帰式の元の値を解釈することが必ずしも意味があるわけではないことに注意してください。
たとえば、プレーヤーがマイナスのポイントを獲得することはできません。
この特定の例では、主に回帰直線の傾きの値2.3095に関心があります。
追加リソース
次のチュートリアルでは、Excel で他の一般的なタスクを実行する方法について説明します。