Excel で標本分布を計算する方法

標本分布は、単一 母集団からの多数の無作為サンプルに基づく特定の統計量の確率分布です。

このチュートリアルでは、Excel で標本分布を使用して次のことを行う方法について説明します。

• 標本分布を生成します。
• 標本分布を視覚化します。
• 標本分布の平均値と標準偏差を計算します。
• 標本分布に関する確率を計算します。

Excel で標本分布を生成する

各標本サイズが20で、平均5.3および標準偏差9の正規分布に基づく、 1,000 個の標本からなる標本分布を生成するとします。

これは、スプレッドシートのセル A2 に次の数式を入力することで簡単に行うことができます。

 = NORM . INV ( RAND (), 5.3, 9)

次に、小さな+が表示されるまでセルの右下隅にカーソルを置き、数式を右 20 セルと下 1000 セルにドラッグします。

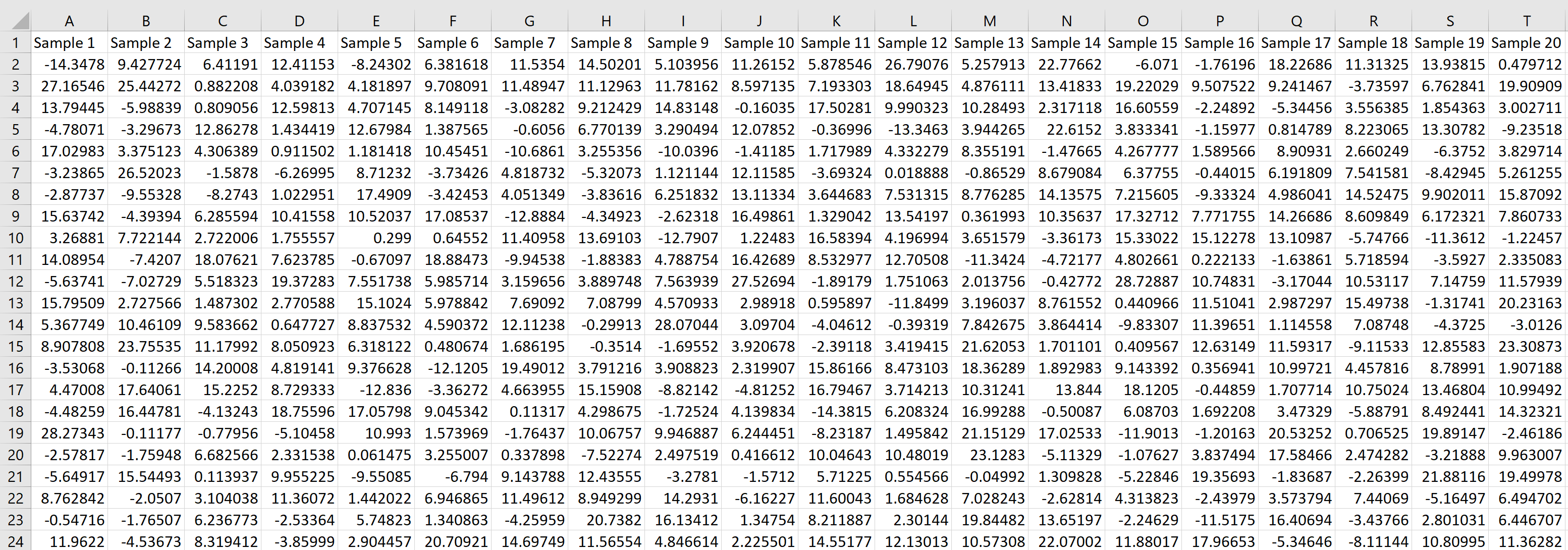
各行はサイズ 20 のサンプルを表し、各値は平均 5.3、標準偏差 9 の正規分布に由来します。

平均と標準偏差を求める

この標本平均値の標本分布の平均値と標準偏差を求めるには、まずワークシートのセル U2 に次の式を入力して各標本の平均値を求めます。

 = AVERAGE (A2:T2)

次に、小さな+が表示されるまでセルの右下隅にカーソルを置き、ダブルクリックしてこの数式を U 列の他のすべてのセルにコピーします。

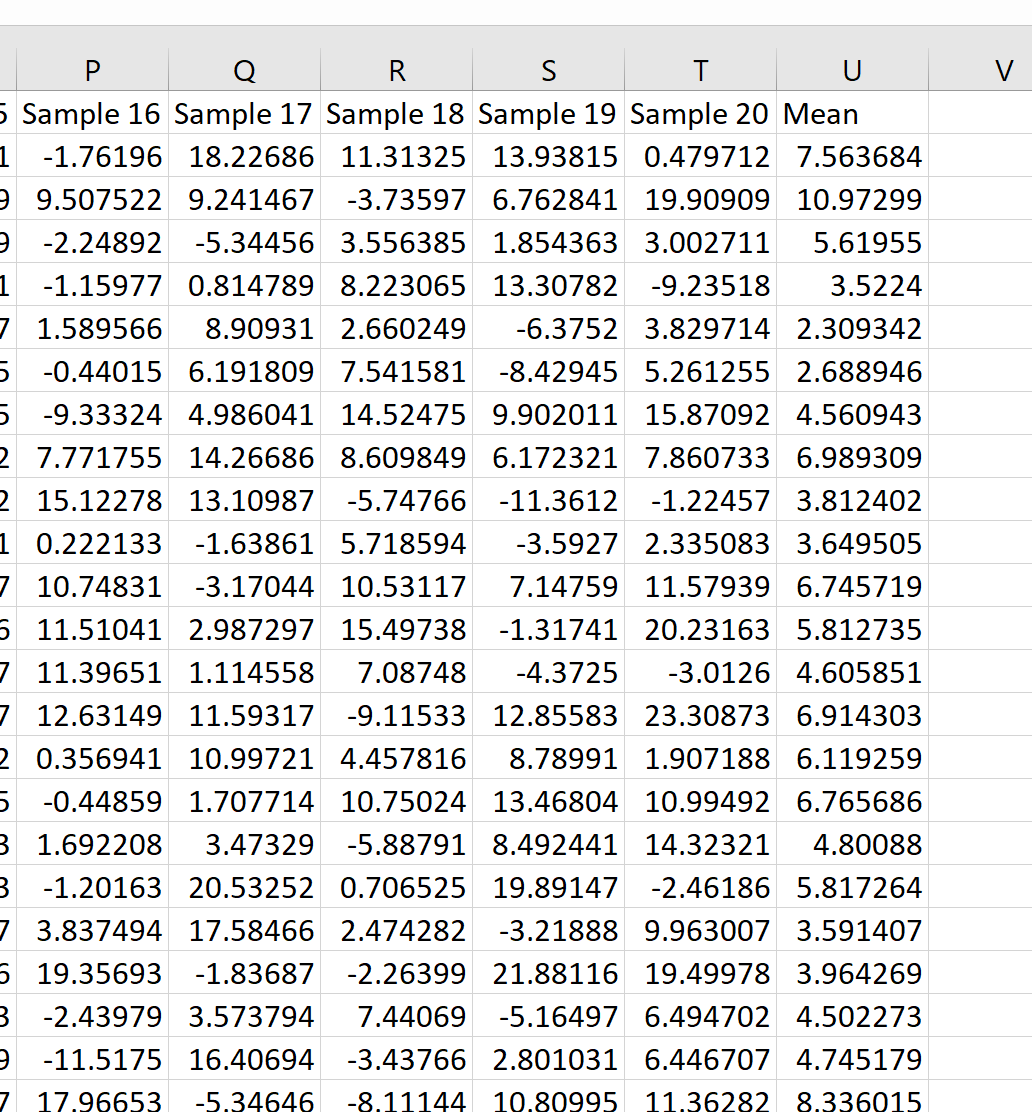
最初のサンプルの平均は 7.563684、2 番目のサンプルの平均は 10.97299 であることがわかります。

次に、次の式を使用して、サンプル平均の平均と標準偏差を計算できます。

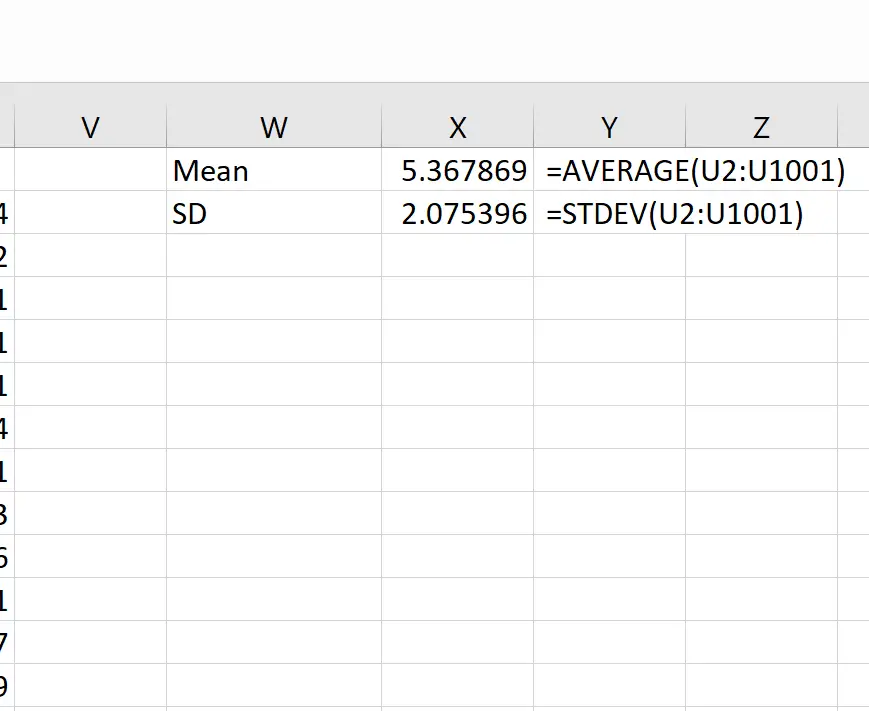
理論的には、標本分布の平均値は5.3になるはずです。この例の実際のサンプル平均は5.367869で、5.3 に近いことがわかります。

そして理論的には、標本分布の標準偏差は s/√n に等しいはずで、9 / √20 = 2.012 となります。標本分布の実際の標準偏差は2.075396で、2.012 に近いことがわかります。

標本分布を視覚化する

単純なヒストグラムを作成して、標本平均値の標本分布を視覚化することもできます。

これを行うには、列 U のすべてのサンプル平均を強調表示し、 [挿入]タブをクリックして、 [グラフ]セクションの[ヒストグラム]オプションをクリックします。

これにより、次のヒストグラムが得られます。

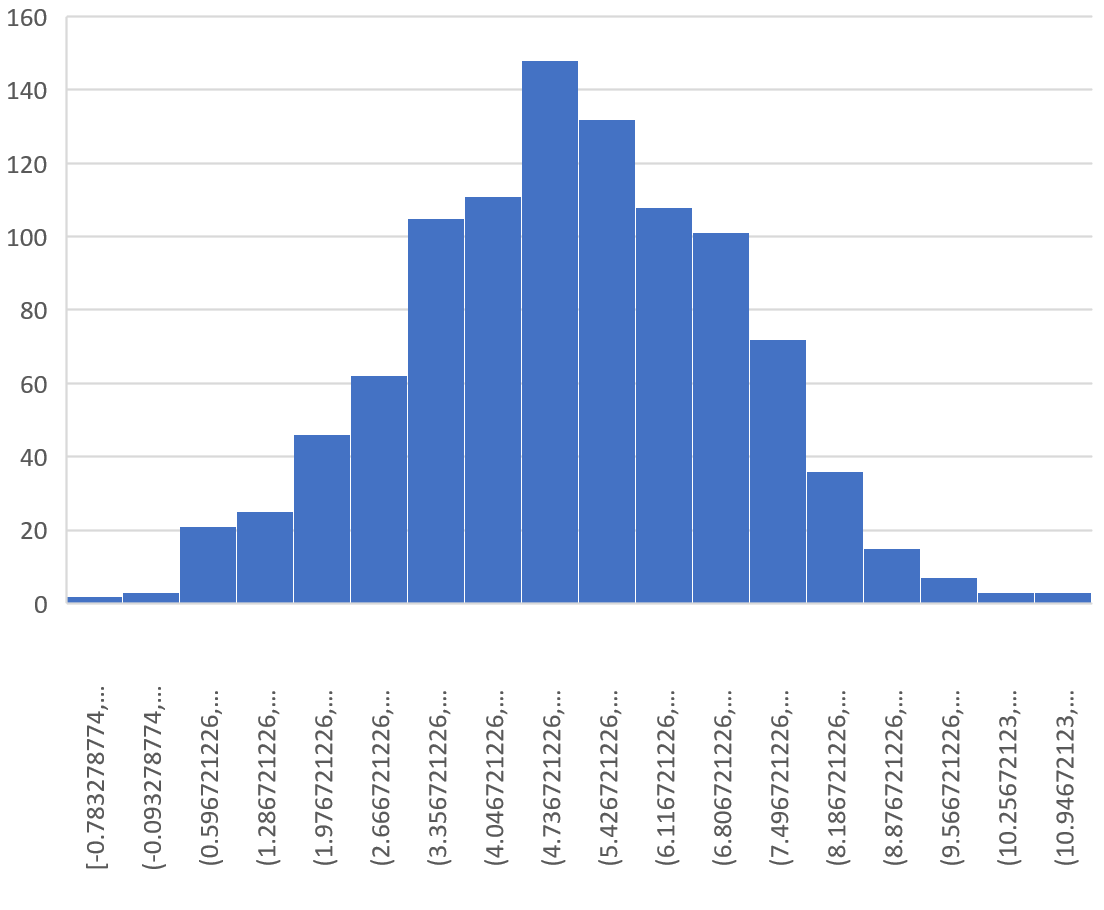
標本分布は値 5 付近にピークを持つ釣鐘型であることがわかります。

ただし、分布の裾から、一部のサンプルの平均値は 10 を超え、他のサンプルの平均値は 0 未満であることがわかります。

確率を計算する

母平均、母標準偏差、サンプルサイズに基づいて、サンプル平均が特定の値を取得する確率を計算することもできます。

たとえば、母集団の平均が 5.3、母集団の標準偏差が 9、サンプル サイズが次の場合、次の式を使用して標本平均が 6 以下である確率を求めることができます。

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

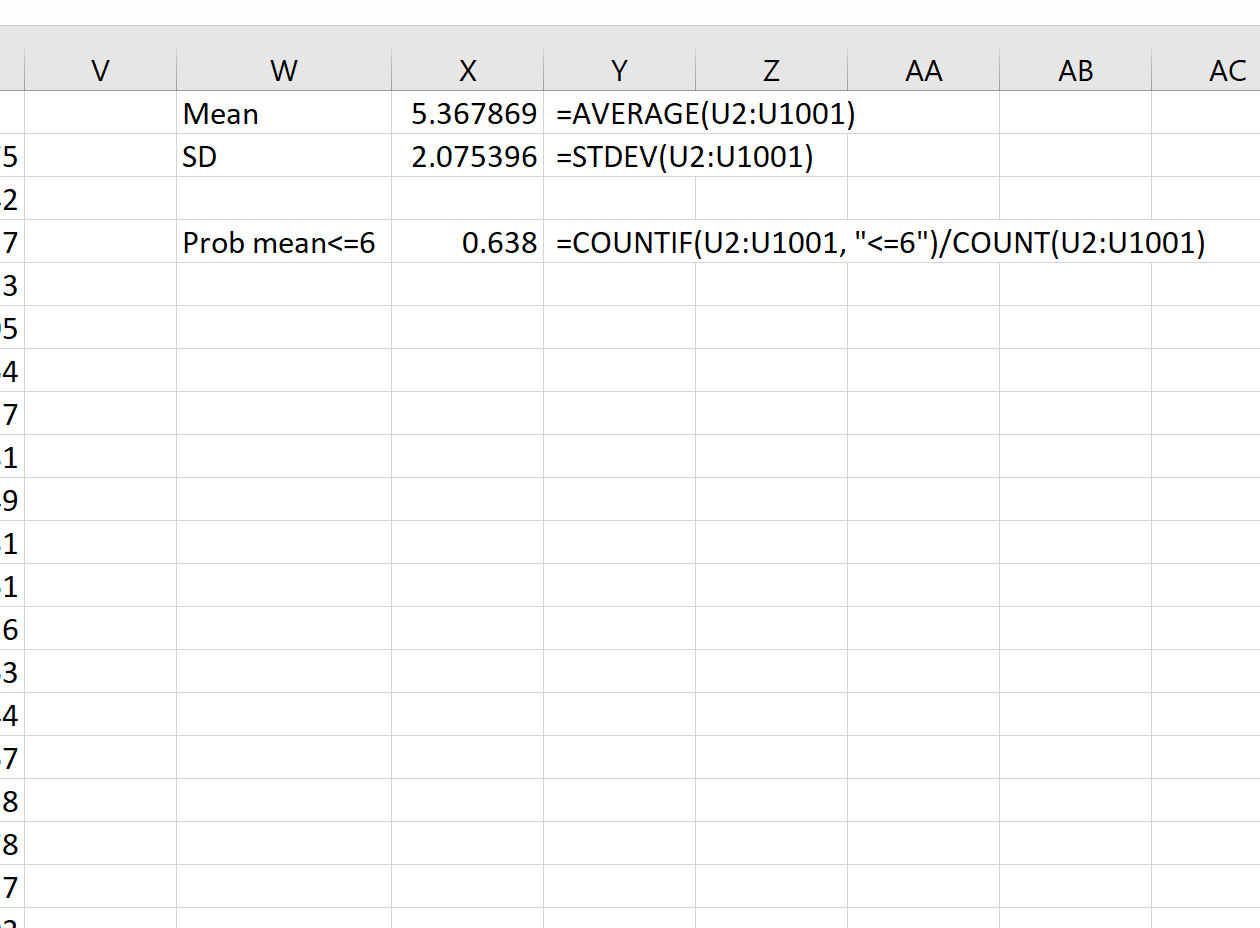
標本平均が 6 以下である確率は0.638 であることがわかります。

これは、 Sampling Distribution Calculatorで計算された確率に非常に近いです。

追加リソース

標本分布の概要
サンプリング分布計算機
中心極限定理の概要