Excel でマン-ホイットニー u 検定を実行する方法

マン-ホイットニー U 検定(ウィルコクソン順位和検定とも呼ばれます) は、標本分布が正規分布しておらず、標本サイズが小さい (n < 30) 場合に、2 つの標本間の差異を比較するために使用されます。

これは、 2 サンプル t 検定と同等のノンパラメトリックとみなされます。

このチュートリアルでは、Excel でマン-ホイットニー U 検定を実行する方法を説明します。

例: Excel でのマン-ホイットニー U 検定

研究者らは、燃料処理によって車の平均燃費が変化するかどうかを知りたいと考えています。これをテストするために、燃料処理を行った 12 台の車と処理を行わなかった 12 台の車の燃費を測定する実験を実施しました。

サンプル サイズが小さく、サンプル分布が正規分布ではないのではないかと考えられるため、マン-ホイットニー U 検定を実行して、2 つのグループ間に mpg に統計的に有意な差があるかどうかを判断することにしました。

Excel でマン-ホイットニー U 検定を実行するには、次の手順を実行します。

ステップ 1: データを入力します。

次のようにデータを入力します。

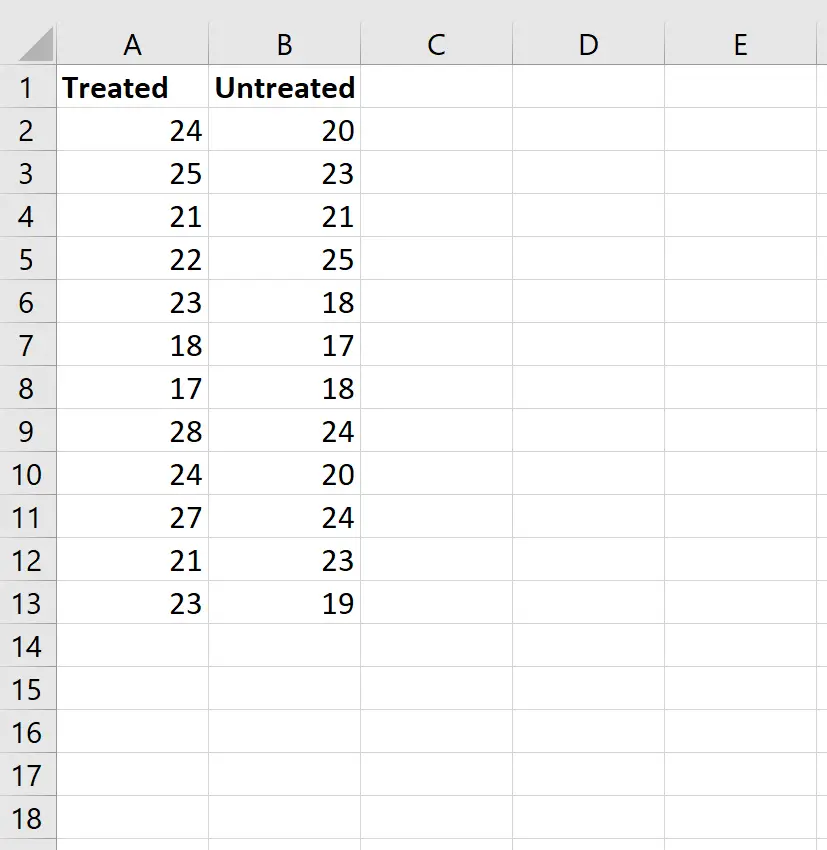
ステップ 2: 両方のグループのランキングを計算します。

次に、各グループのランキングを計算します。次の図は、処理済みグループの最初の値のランクを計算するために使用する式を示しています。

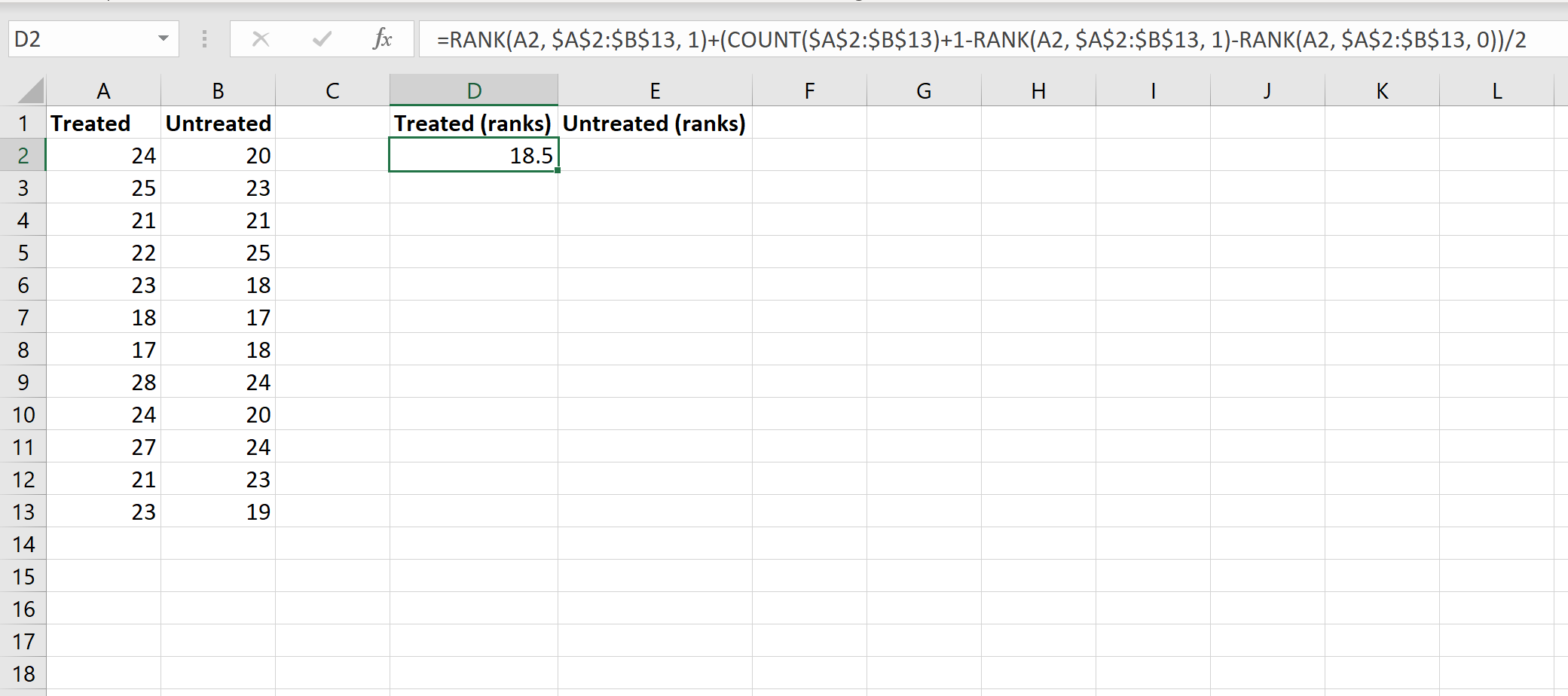
この式は非常に複雑ですが、入力する必要があるのは 1 回だけです。次に、数式を他のすべてのセルにドラッグするだけで、行を埋めることができます。

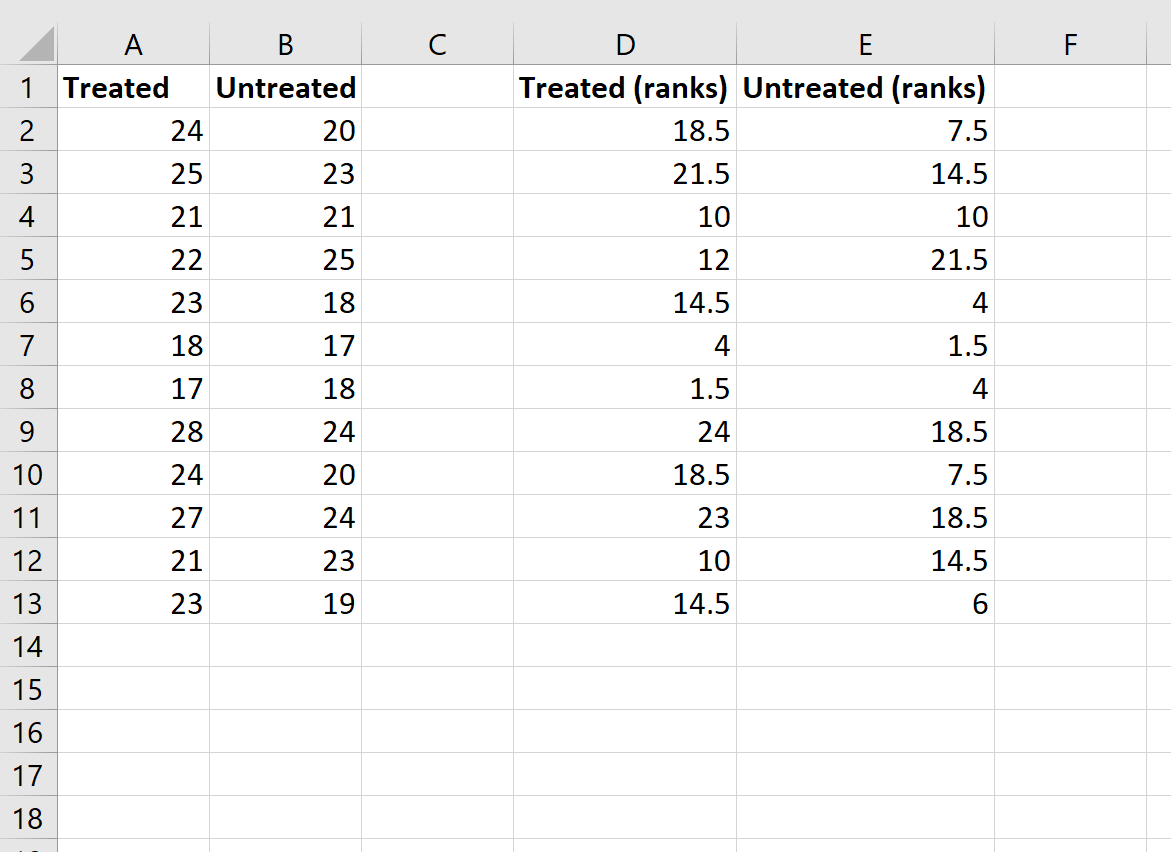
ステップ 3: 検定統計量に必要な値を計算します。

次に、次の式を使用して、各グループのランクの合計、各グループのサンプル サイズ、各グループの U 検定統計量、および全体の U 検定統計量を計算します。

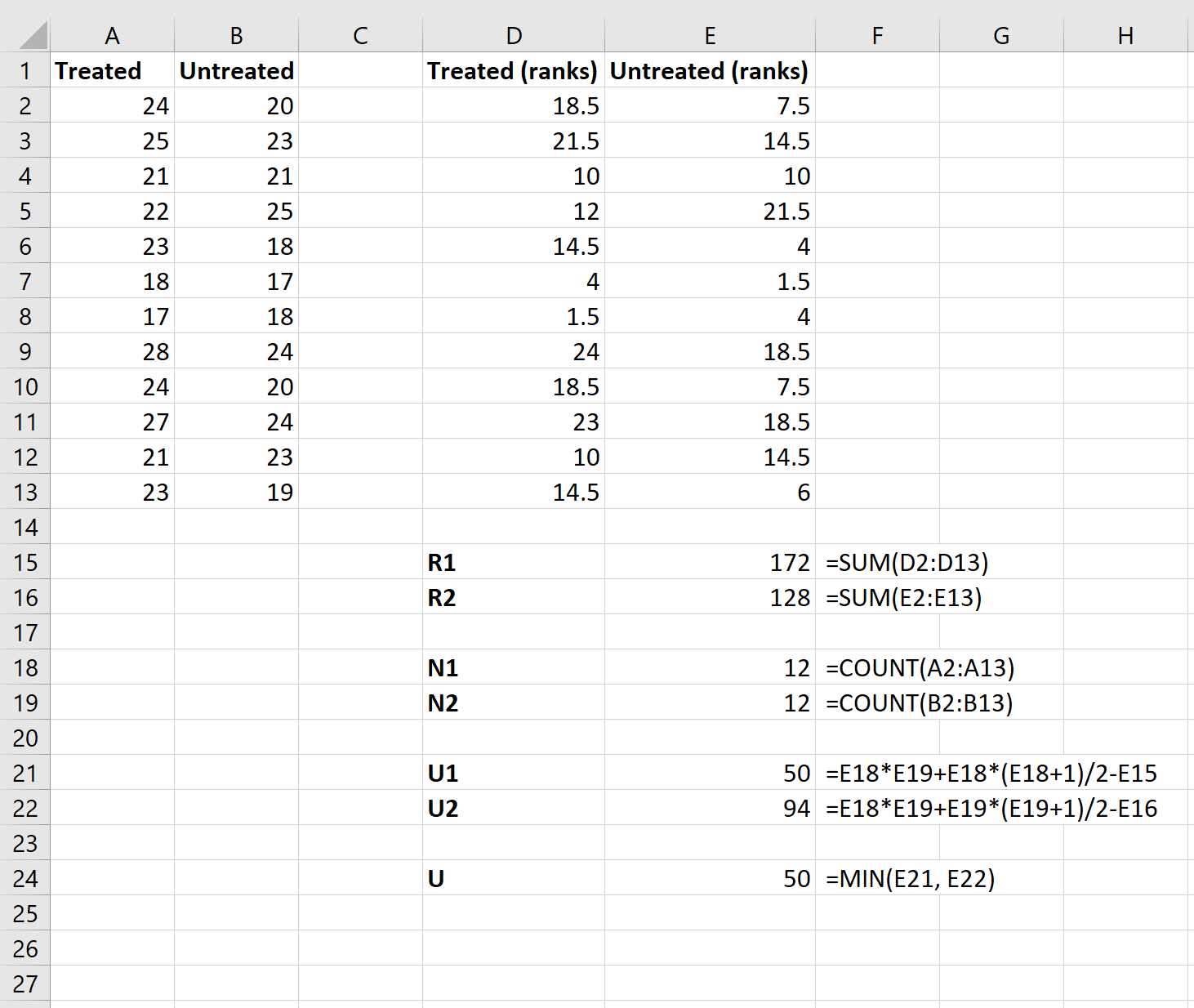
ステップ 4: Z 検定統計量と対応する p 値を計算します。

最後に、次の式を使用して Z 検定統計量と対応するp 値を計算し、帰無仮説を棄却すべきかどうかを決定します。

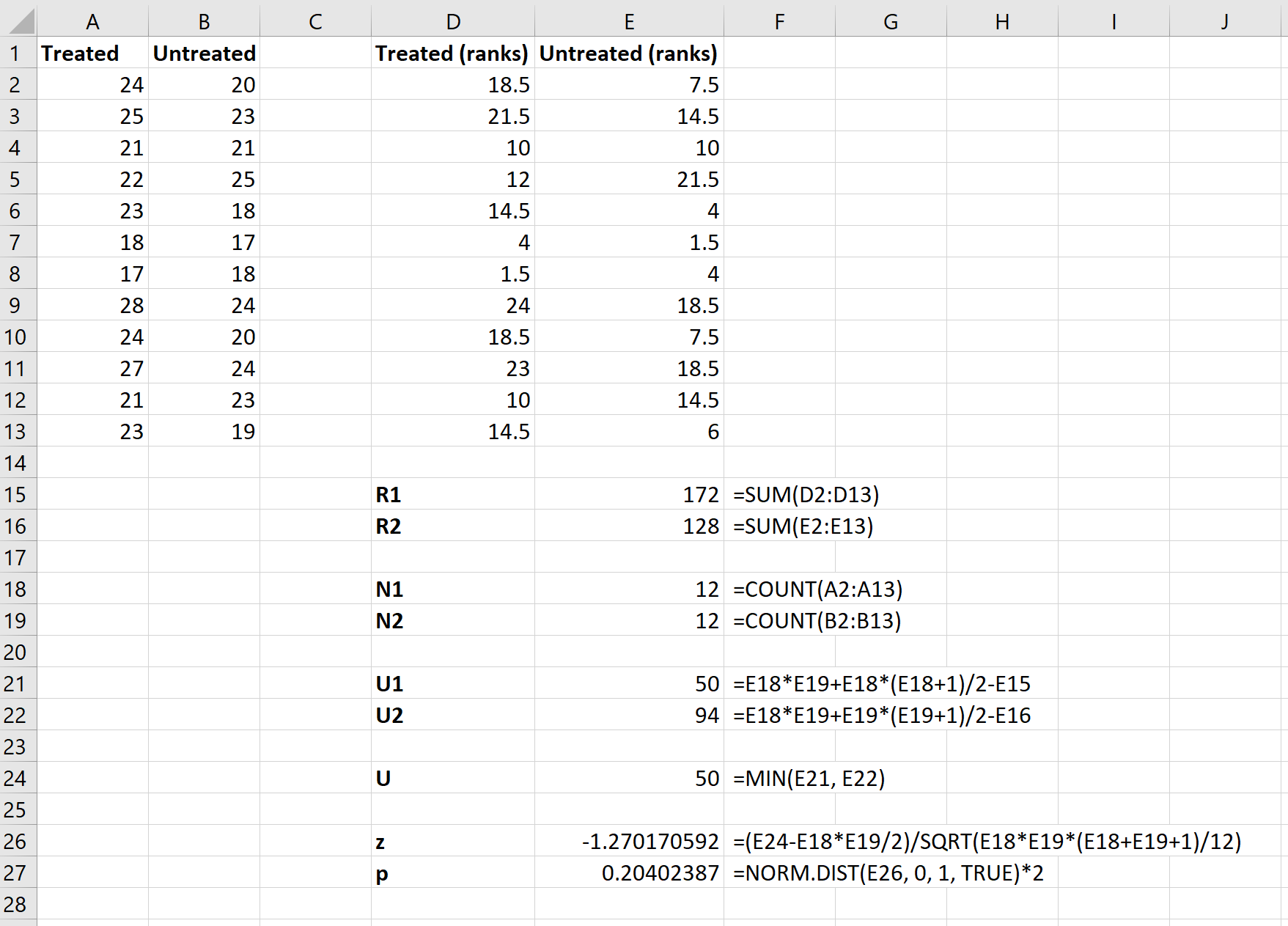
検定の帰無仮説は、両方のグループの平均 mpg が同じであることを示します。検定の p 値 ( 0.20402387 ) は有意水準 0.05 を下回らないため、帰無仮説を棄却できません。

真の平均mpgが2つのグループ間で異なると言える十分な証拠はありません。