Excel: linest 関数の出力を解釈する方法

LINEST関数を使用すると、Excel で回帰モデルを近似できます。

この関数は次の基本構文を使用します。

 LINEST(known_y's, known_x's, const, stats)

金：

• known_y : 応答変数の値の列
• known_x : 予測子変数の値の 1 つ以上の列
• const : TRUE = 通常どおりインターセプトを計算します、FALSE = インターセプトを強制的にゼロにします
• stats : TRUE = 追加の回帰統計を計算する、FALSE = 係数のみを計算する

次の例は、 LINEST関数の出力を実際に解釈する方法を示しています。

例: Excel で LINEST 出力を解釈する方法

予測変数 (x) と応答変数 (y) を含む次のデータセットがあるとします。

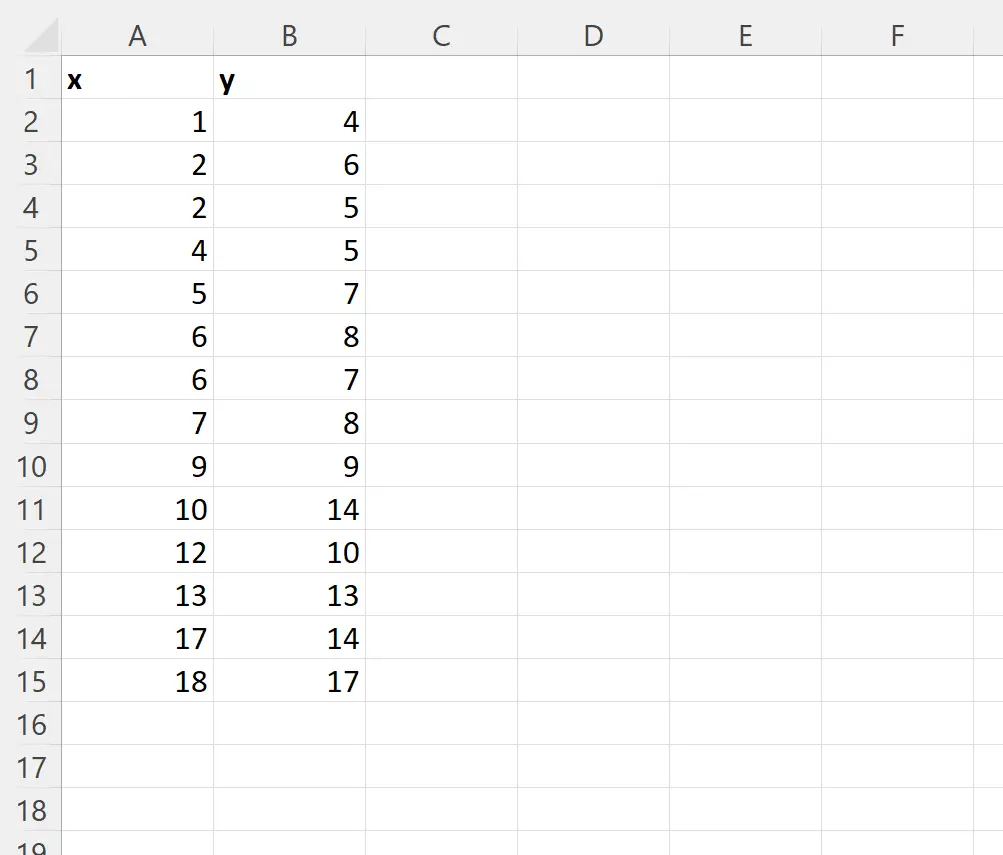
セルD1に次の数式を入力して、このデータ セットを使用して単純な線形回帰を実行できます。

 =LINEST( A2:A15 , B2:B15 , TRUE, TRUE)

LINEST関数の出力には、回帰モデルの係数といくつかの追加統計が含まれています。

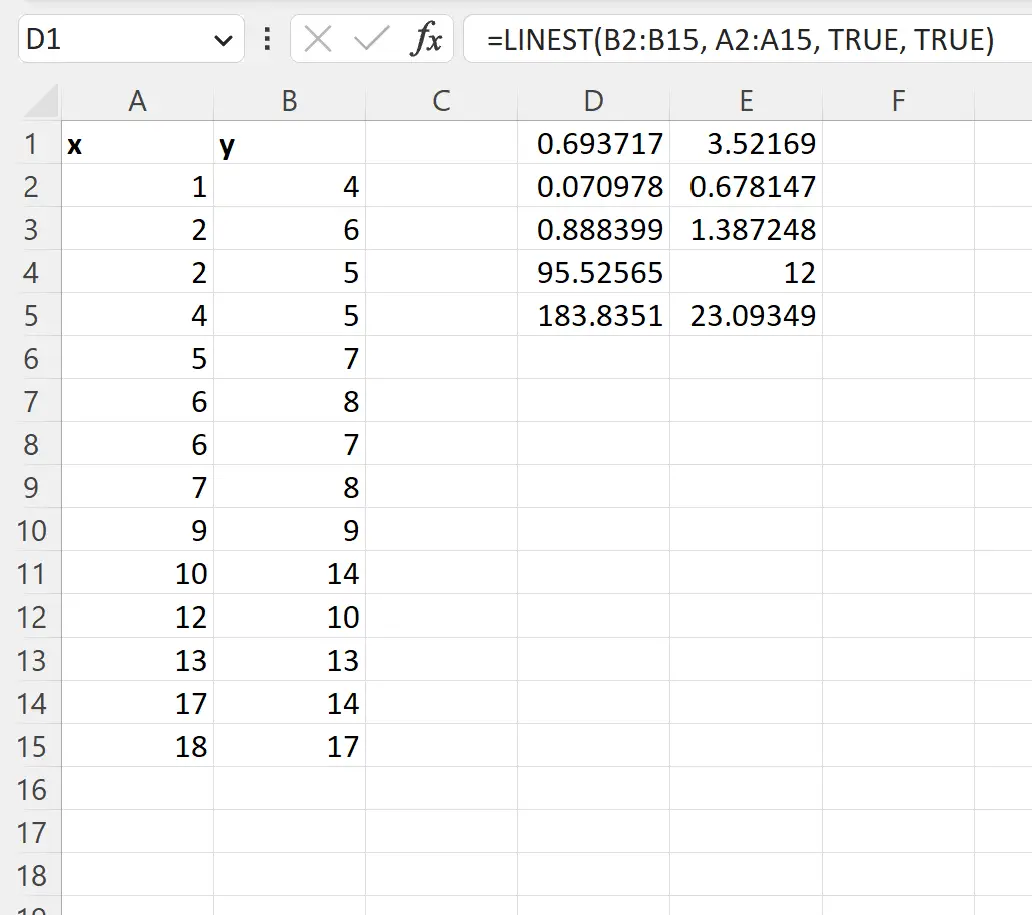
次のスクリーンショットは、結果の各値の説明を示しています。

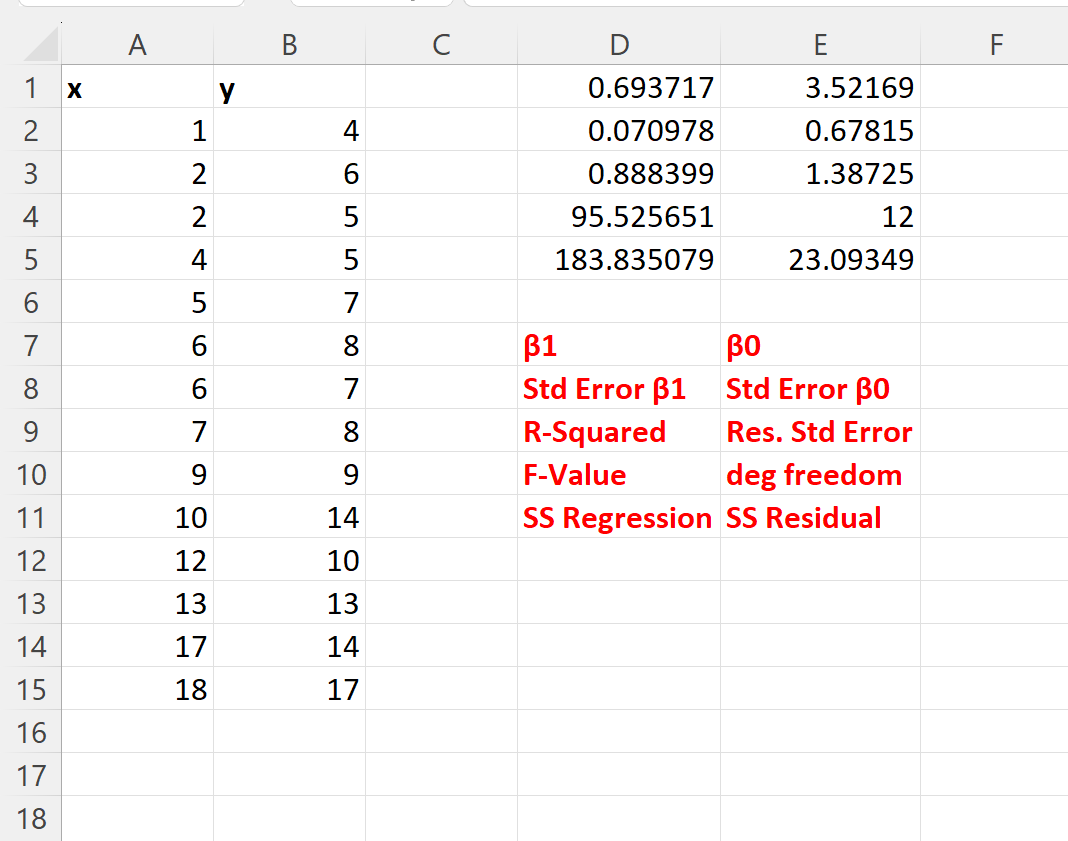
結果から次のことがわかります。

• β ₀の係数は3.52169です。
• _β1の係数は0.693717です。

これらの値を使用すると、この単純な回帰モデルの方程式を書くことができます。

y = 3.52169 + 0.693717(x)

これは、予測変数 x が 1 単位増加するたびに、応答変数 y の平均0.693717の増加が関連付けられることを意味すると解釈します。

元の用語は、 x がゼロの場合、 y の平均値は3.52169であることを意味すると解釈します。

次のことも確認できます。

• モデルの R 二乗値は0.888です。

これは、予測変数がモデル応答変数の変動の88.8%を説明できることを意味すると解釈します。

関連:適切な R 二乗値とは何ですか?

追加リソース

次のチュートリアルでは、Excel での回帰に関する追加情報を提供します。

Excelでの回帰出力のP値を解釈する方法
Excel の散布図に回帰直線を追加する方法
Excel で多項式回帰を実行する方法