Excel で normalcdf 確率を計算する方法

TI-83 または TI-84 計算機のNormalCDF関数を使用すると、正規分布確率変数が特定の範囲内の値を取る確率を見つけることができます。

TI-83 または TI-84 計算機では、この関数は次の構文を使用します。

Normalcdf (下限、上限、μ、σ)

金：

• lower = 範囲の下限値
• upper = 範囲の上限値
• μ = 母平均
• σ = 母標準偏差

たとえば、確率変数が平均 50、標準偏差 4 で正規分布しているとします。確率変数が 48 ～ 52 の値を取る確率は、次のように計算できます。

Normalcdf(48, 52, 50, 4) = 0.3829

次の構文を使用するNORM.DIST()関数を使用して、この応答を Excel で再現できます。

NORM.DIST(x、σ、μ、累積)

金：

• x = 個々のデータ値
• μ = 母平均
• σ = 母標準偏差
• 累積 = FALSE PDF を計算します。 TRUE は CDF を計算します

次の例は、この関数を実際に使用する方法を示しています。

例 1: 2 つの値の間の確率

確率変数が平均 50、標準偏差 4 で正規分布しているとします。確率変数が 48 ～ 52の値を取る確率は、次のように計算できます。

 =NORM. DIST (52, 50, 4, TRUE ) - NORM. DIST (48, 50, 4, TRUE )

次の図は、Excel でこの計算を実行する方法を示しています。

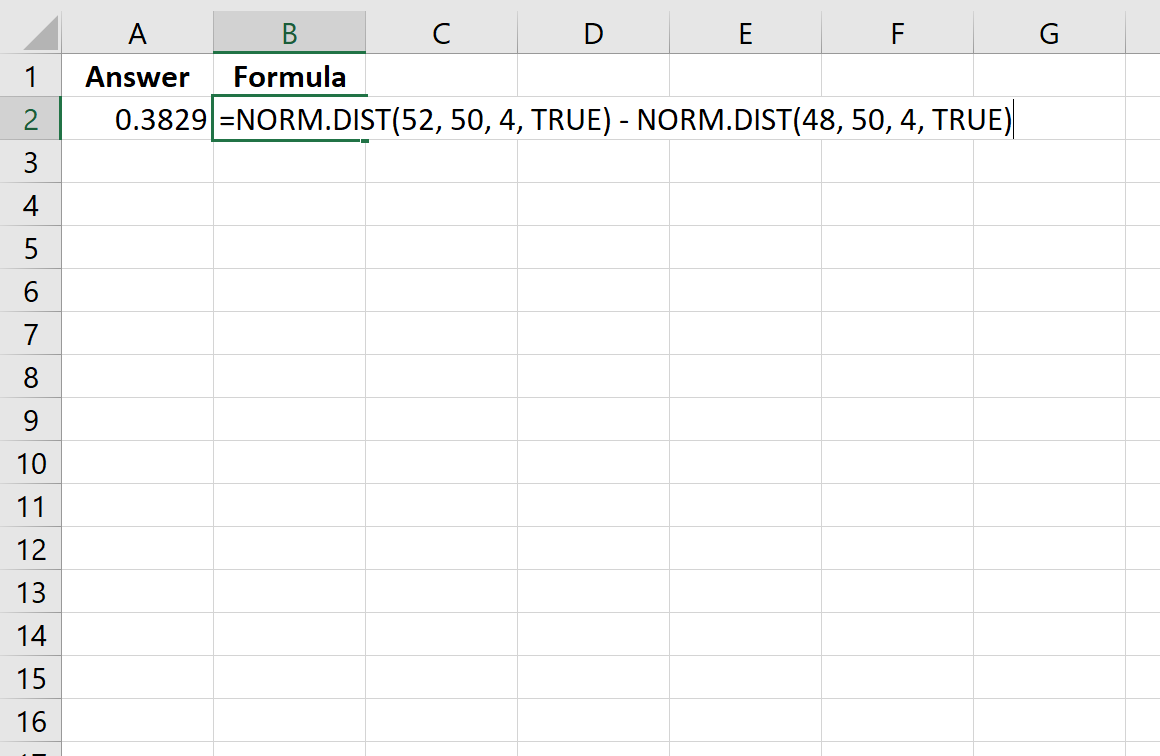
確率は0.3829 であることがわかります。

例 2: 1 つの値未満の確率

確率変数が平均 50、標準偏差 4 で正規分布していると仮定します。確率変数が 48未満の値をとる確率は、次のように計算できます。

 =NORM. DIST (48, 50, 4, TRUE )

次の図は、Excel でこの計算を実行する方法を示しています。

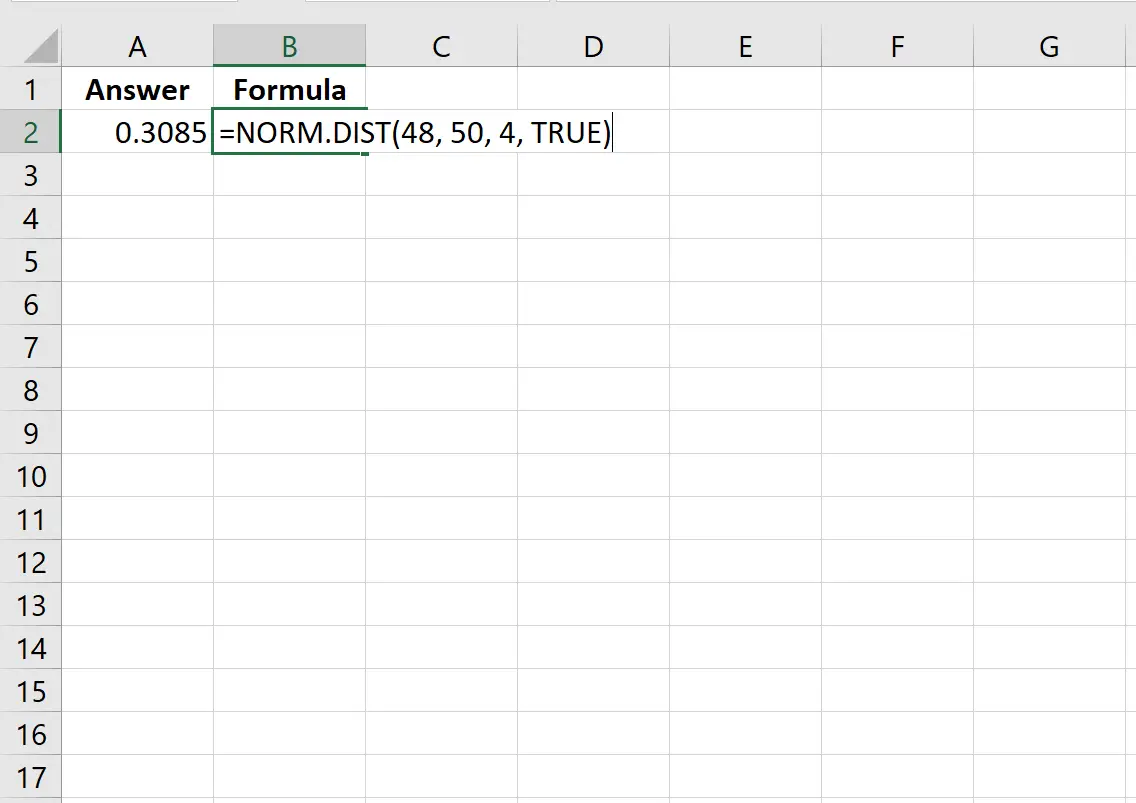
確率は0.3085 であることがわかります。

例 3: ある値を超える確率

確率変数が平均 50、標準偏差 4 で正規分布しているとします。確率変数が 55より大きい値を取る確率は、次のように計算できます。

 =1 - NORM. DIST (55, 50, 4, TRUE )

次の図は、Excel でこの計算を実行する方法を示しています。

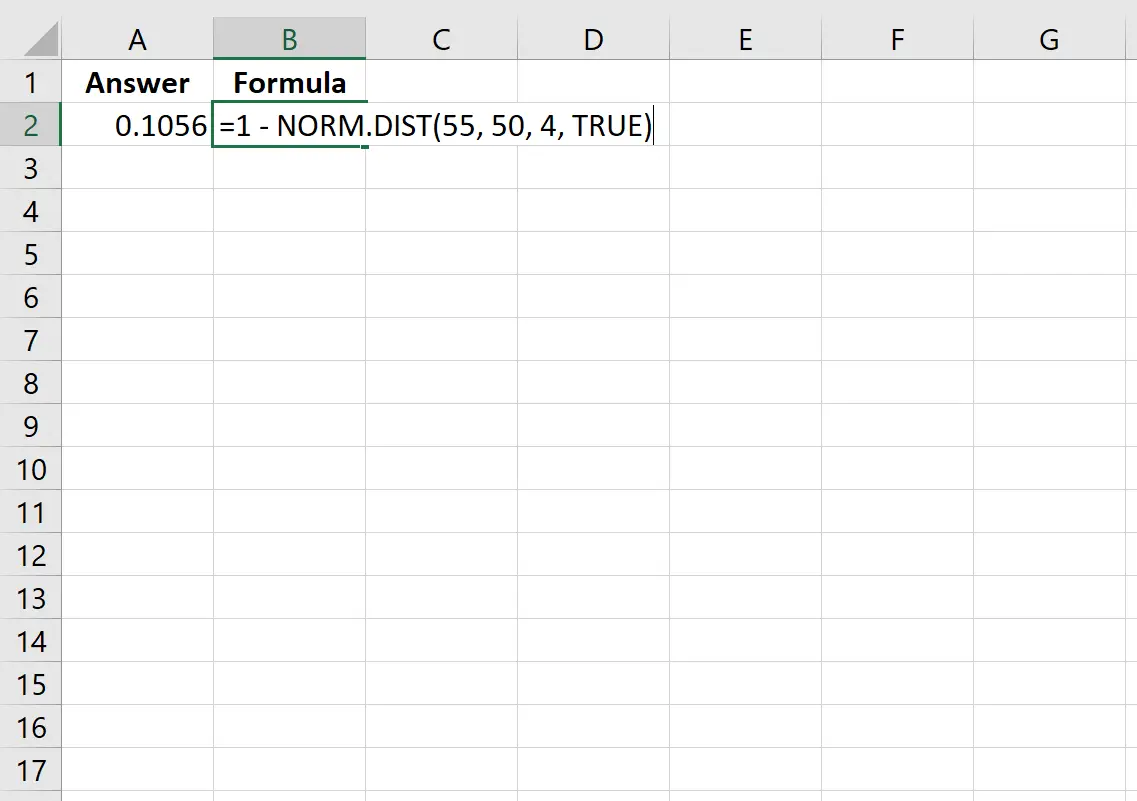
確率は0.1056 であることがわかります。

追加リソース

この正規 CDF 計算ツールを使用して、正規分布に関連付けられた確率を自動的に見つけることもできます。