Excel で予測間隔を作成する方法

統計学において、単純線形回帰は、予測変数 x と応答変数 y の間の関係を定量化するために使用できる手法です。

単純な線形回帰を実行すると、x と y の関係を表す「最適な直線」が得られます。これは次のように記述できます。

ŷ = b ₀ + b ₁ x

金：

• ŷ は応答変数の予測値です
• b _{0 は}y 切片です
• b ₁は回帰係数です
• x は予測子変数の値です

場合によっては、この最適直線を使用して、特定の x ₀の値に対する予測区間を構築したいことがあります。これは、母集団内の y の真の値が 95% の確率で一致するような、予測値 ŷ ₀の周囲の区間です。 x ₀に対応する はこの区間に含まれます。

特定の値 x ₀の予測区間を計算する式は次のように記述されます。

ŷ ₀ +/- t _α/2,df=n-2 * se

金：

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

数式は少し難しそうに見えますが、Excel で計算するのは簡単です。次に、この数式を使用して Excel で特定の値の予測区間を計算する例を見ていきます。

例: Excel で予測間隔を構築する方法

次のデータセットは、15 人の異なる学生が取得した試験のスコアと学習時間数を示しています。

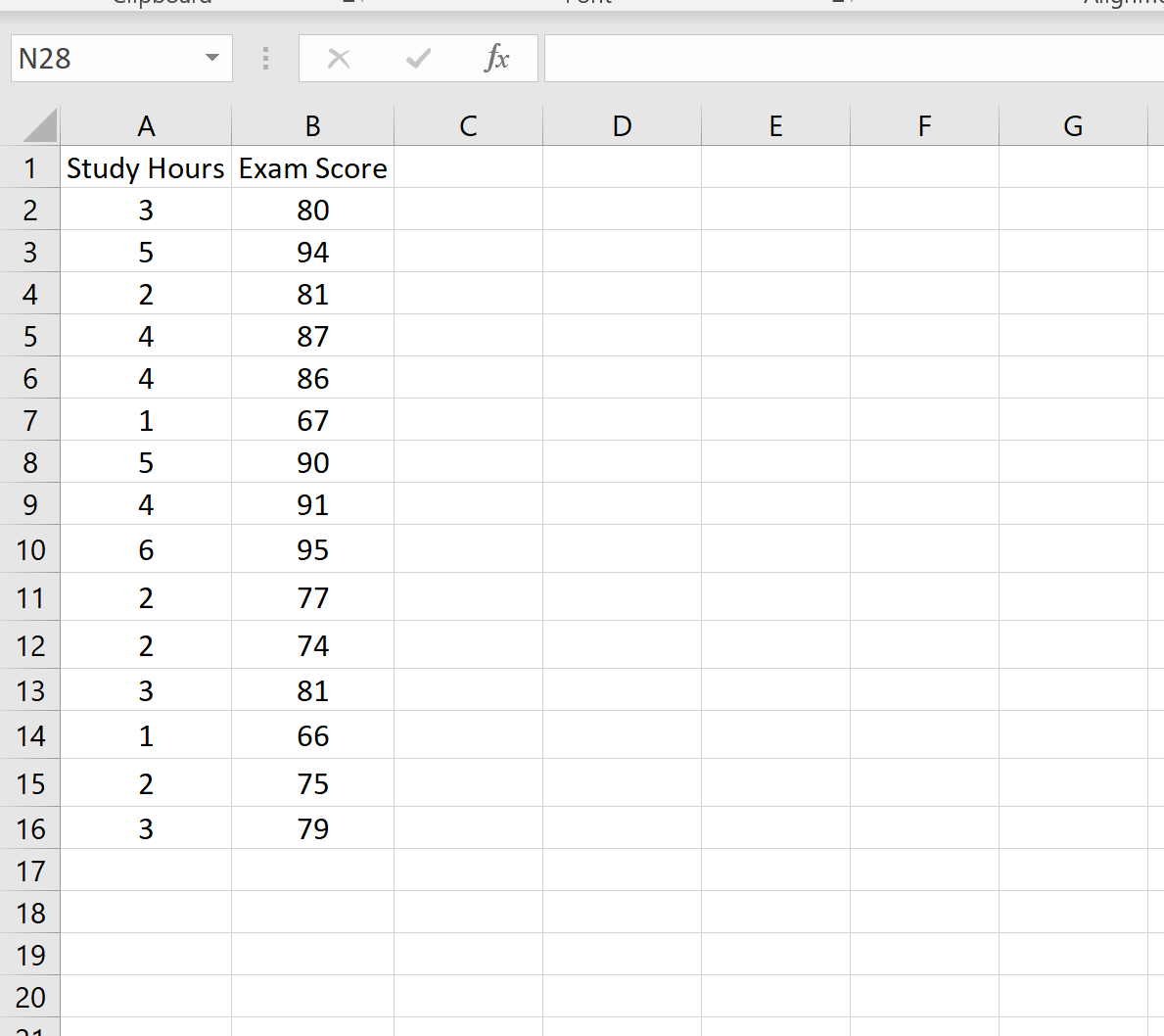
値 x ₀ = 3 に対して 95% の予測区間を作成したいとします。つまり、試験のスコアが 95% の確率でこの区間内に勉強する学生のような区間を作成したいとします。 3時間。

次のスクリーンショットは、この予測間隔を取得するために必要なすべての値を計算する方法を示しています。

注:列Fの数式は、列Eの値がどのように計算されたかを示しています。

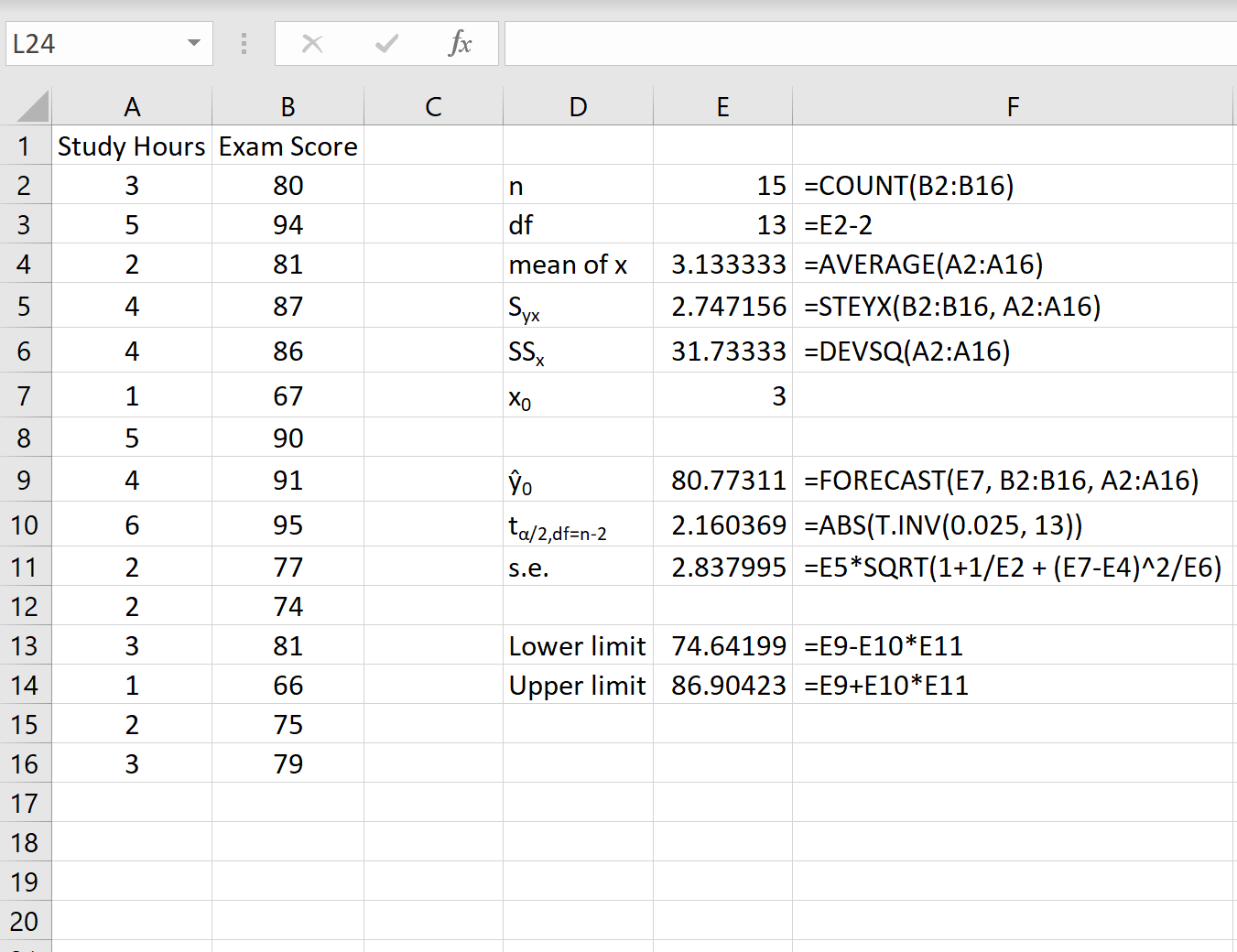
x ₀ = 3 の値の 95% 予測区間は(74.64, 86.90)です。つまり、3 時間勉強した生徒は 74.64 ～ 86.90 のスコアを取得すると 95% の確率で予測します。

使用される計算に関するいくつかのメモ:

• t _{α/2,df=n-2 の t 臨界値を計算するには、} 95% の予測間隔が必要なので、α/2 = 0.05/2 = 0.25 を使用しました。予測間隔 (99% 予測間隔など) を高くすると、間隔が広くなることに注意してください。逆に、予測間隔が小さくなると (90% 予測間隔など)、間隔は狭くなります。
• 式=FORECAST()を使用して ŷ ₀の予測値を取得しましたが、式=FORECAST.LINEAR() はまったく同じ値を返します。