Excel: 回帰係数の信頼区間を計算する

線形回帰モデルでは、 回帰係数によって、予測変数の 1 単位の増加に関連する応答変数の平均変化がわかります。

次の式を使用して、回帰係数の信頼区間を計算できます。

β ₁の信頼区間: b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

金：

•   b ₁ = 回帰表に示されている回帰係数
• t _{1-∝/2, n-2} = n-2 自由度の 1-∝ 信頼水準の臨界 t 値。nはデータセット内の観測値の総数です。
• se(b ₁ ) = 回帰表に示される b ₁の標準誤差

次の例は、Excel で回帰係数の信頼区間を計算する方法を示しています。

例: Excel の回帰係数の信頼区間

特定のクラスの 15 人の生徒について、学習時間を予測変数として使用し、試験の得点を応答変数として使用して、単純な線形回帰モデルを近似したいとします。

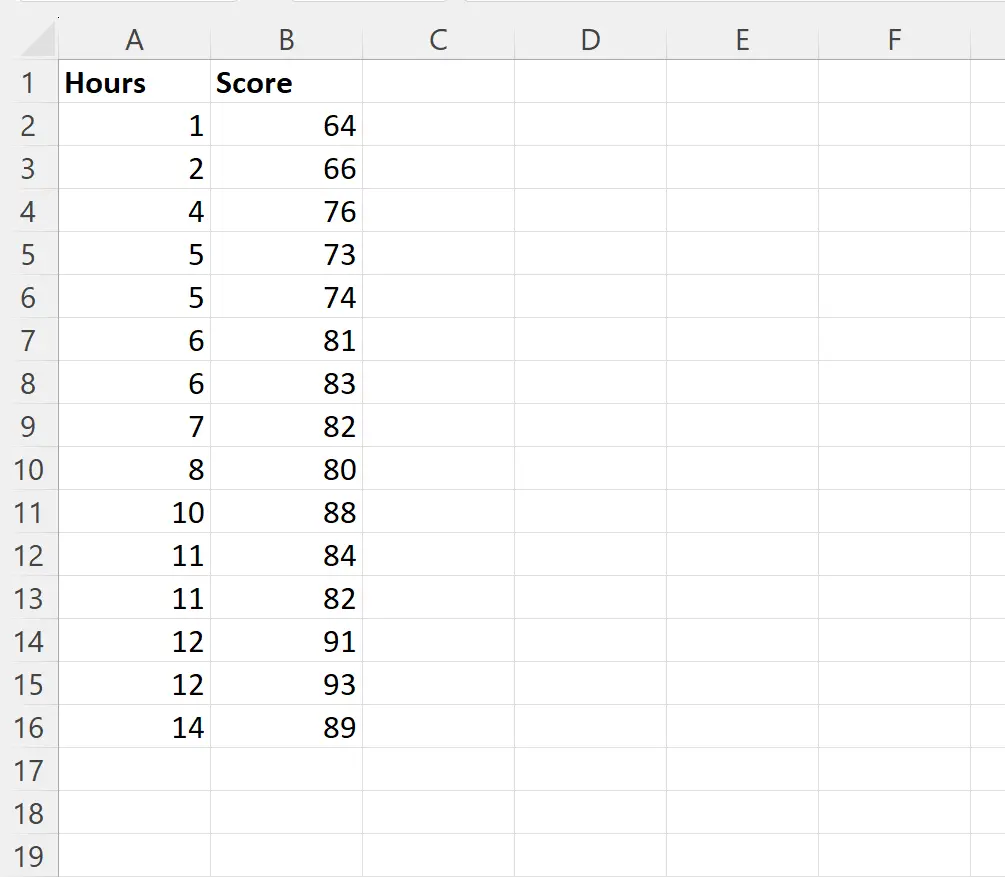
セル D2 に次の式を入力すると、時間列の値を予測変数として使用し、スコア列の値を応答変数として使用して単純な線形回帰を実行できます。

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

最初のTRUE引数は、回帰式の切片を強制的にゼロにすることなく通常どおり計算するように Excel に指示することに注意してください。

2 番目のTRUE引数は、係数に加えて追加の回帰統計を生成するように Excel に指示します。

次のスクリーンショットは、この式の結果を示しています (出力の下の赤いテキストで各出力値が何を表すかを説明しています)。

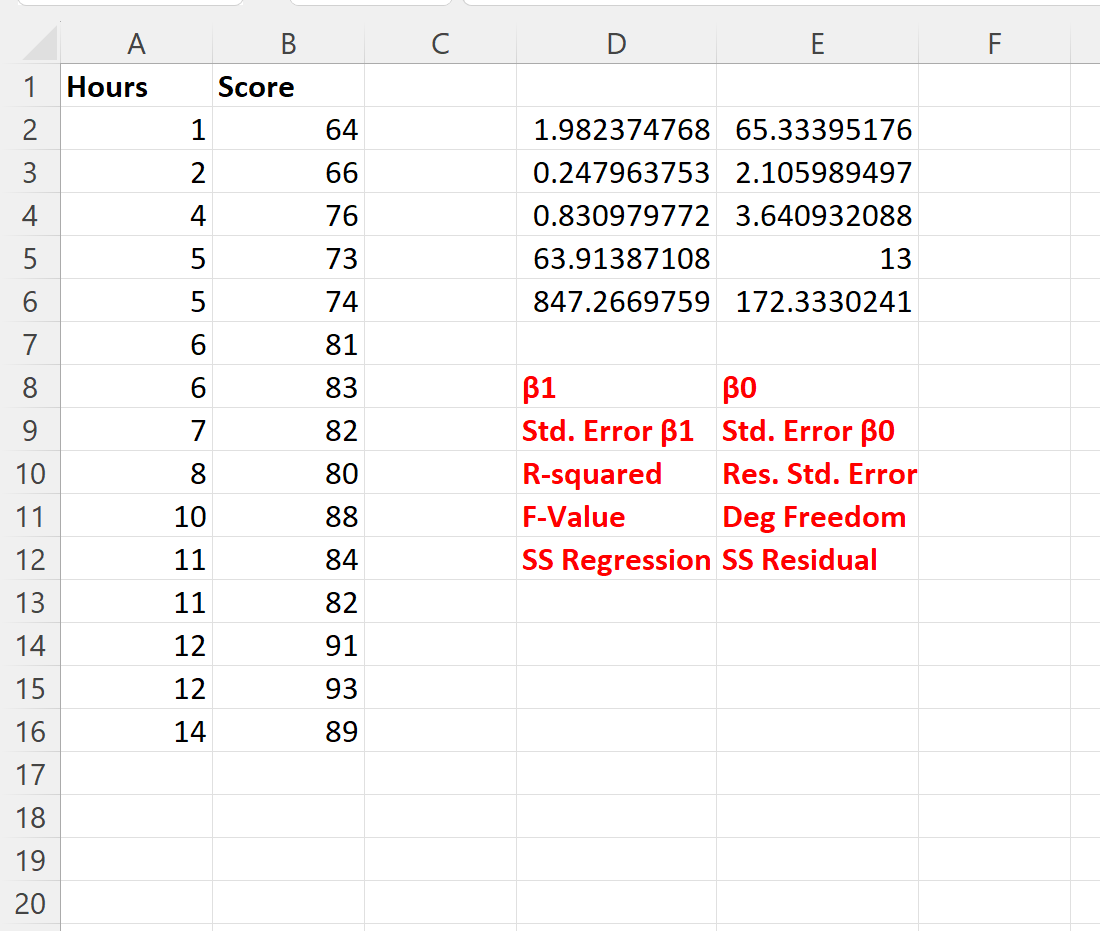
回帰係数を使用すると、次のように近似回帰式を書くことができます。

スコア = 65.334 + 1.982*(学習時間)

時間の回帰係数は1.982であることに注意してください。

これは、学習時間が 1 時間増えるごとに、試験のスコアが平均1,982点増加することを示しています。

回帰係数の 95% 信頼区間を計算するには、セル H2 と H3 に次の式を入力します。

• H2: = D2 – T.INV.2T(0.05, E5)*D3
• H3: = D2 + T.INV.2T(0.05, E5)*D3

次のスクリーンショットは、これらの数式を実際に使用する方法を示しています。

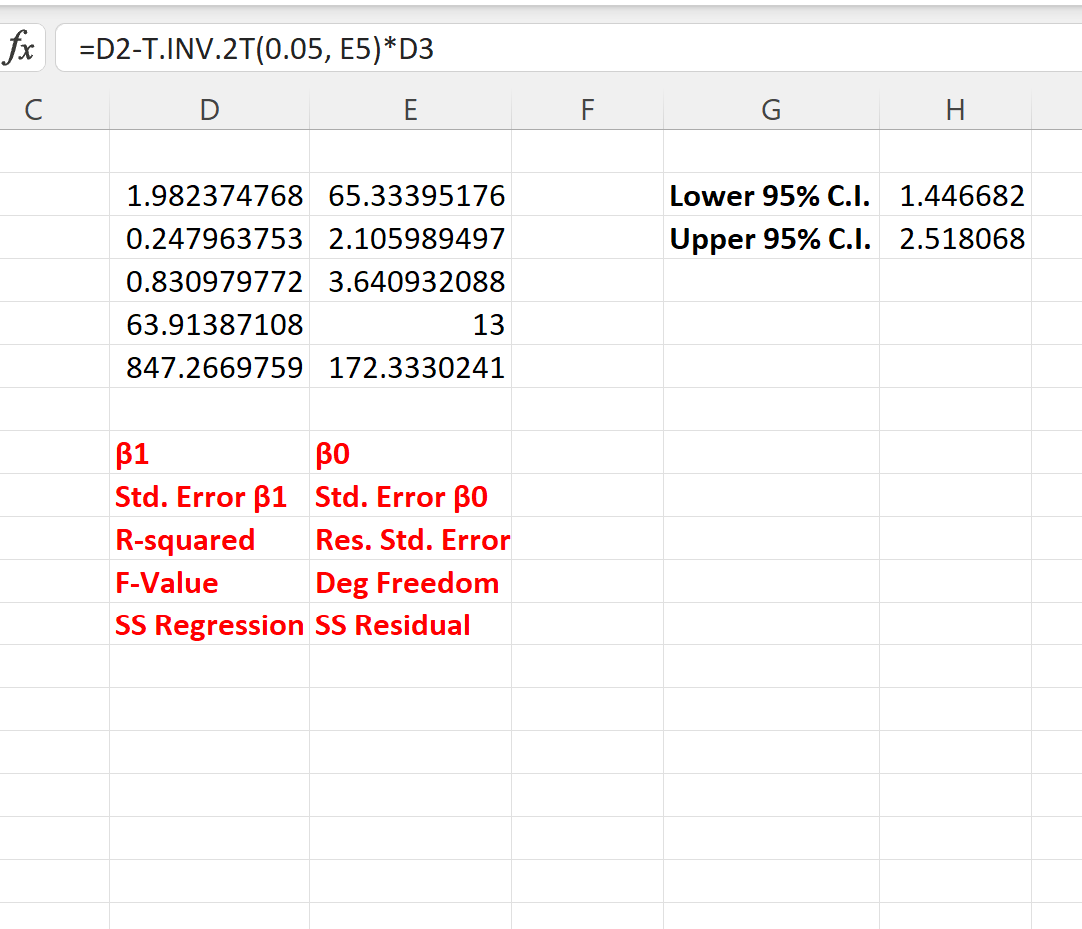
回帰係数の 95% 信頼区間は[1.446, 2.518]です。

この信頼区間には値 0 が含まれていないため、学習時間と試験の成績の間には統計的に有意な関連があると結論付けることができます。

回帰係数の 95% 信頼区間を手動で計算することによって、これが正しいことを確認することもできます。

• β ₁の 95% CI: b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• β ₁の 95% CI: 1.982 ± t _0.975、15-2 * 0.248
• β ₁の 95% CI: 1.982 ± 2.1604 * 0.248
• β ₁の 95% CI: [1.446, 2.518]

回帰係数の 95% 信頼区間は[1.446, 2.518]です。

追加リソース

次のチュートリアルでは、Excel で他の一般的なタスクを実行する方法について説明します。

Excelで単純な線形回帰を実行する方法
Excelで重回帰を実行する方法
Excelでの回帰出力のP値を解釈する方法