Excel: linest を使用して重線形回帰を実行する方法

Excel でLINEST関数を使用すると、重線形回帰モデルをデータ セットに適合させることができます。

この関数は次の基本構文を使用します。

 = LINEST ( known_y's, [known_x's], [const], [stats] )

金：

• known_y : 既知の y 値の配列
• known_x : 既知の x 値の配列
• const : オプションの引数。 TRUE の場合、定数 b は通常どおり処理されます。 FALSE の場合、定数 b は 1 に設定されます。
• stats : オプションの引数。 TRUE の場合、追加の回帰統計が返されます。 FALSE の場合、追加の回帰統計は返されません。

次のステップバイステップの例は、この関数を実際に使用する方法を示しています。

ステップ 1: データを入力する

まず、次のデータセットを Excel に入力してみましょう。

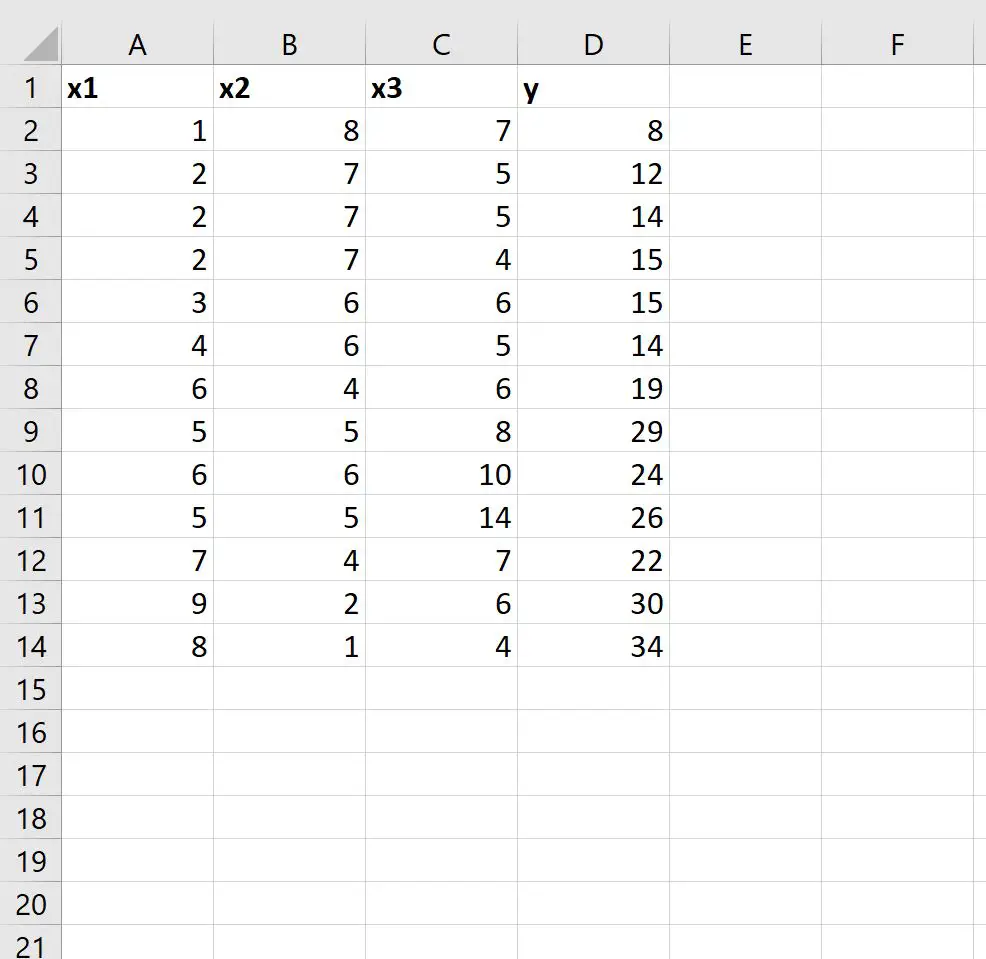
ステップ 2: LINEST を使用して重線形回帰モデルを近似する

x1 、 x2 、およびx3を予測子変数として、 yを応答変数として使用して重線形回帰モデルを近似したいとします。

これを行うには、任意のセルに次の数式を入力して、この重線形回帰モデルに適合させます。

 =LINEST( D2:D14 , A2:C14 )

次のスクリーンショットは、この式を実際に使用する方法を示しています。

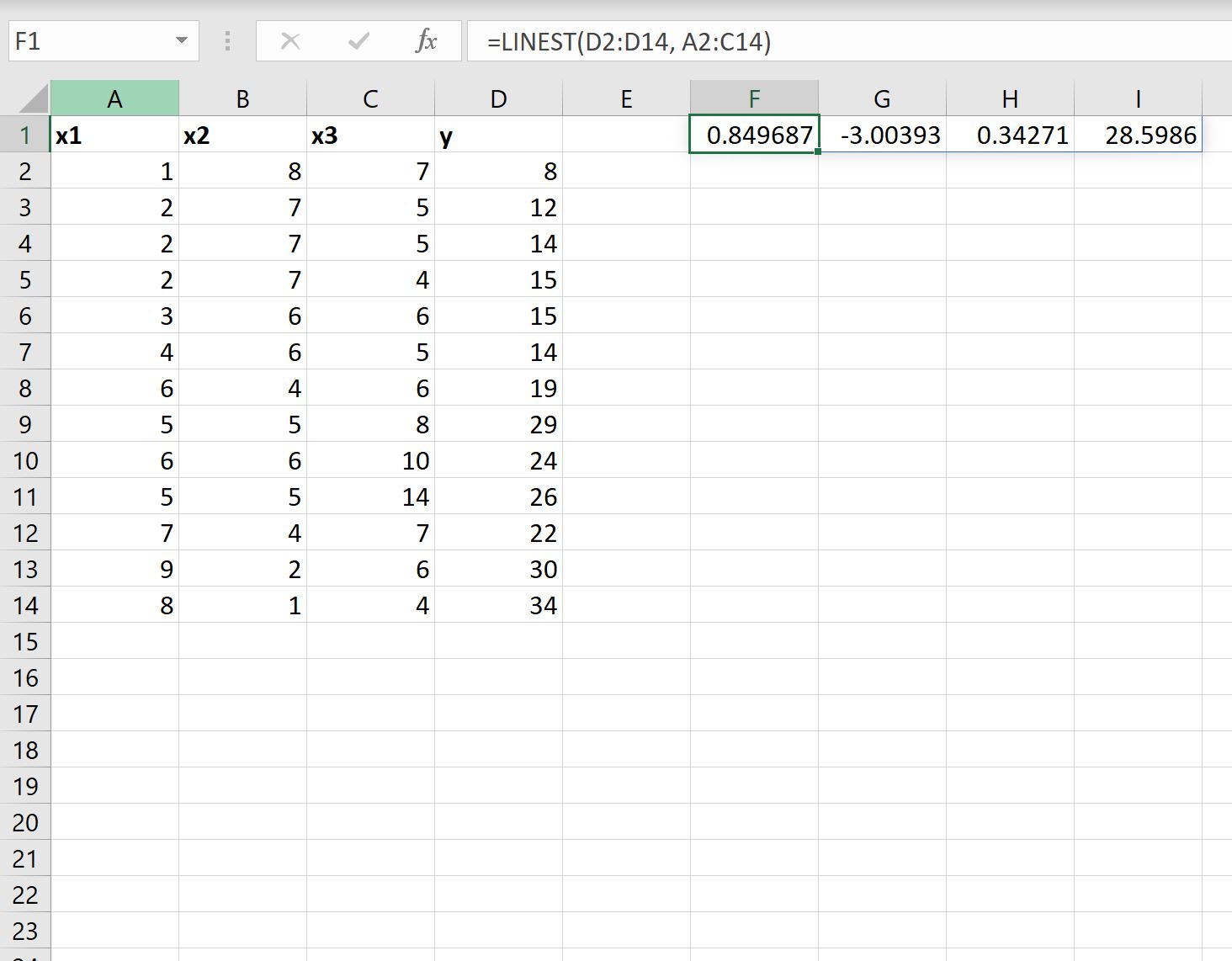
結果を解釈する方法は次のとおりです。

• 切片の係数は28.5986です。
• x1 の係数は0.34271です。
• x2 の係数は-3.00393です。
• x3 の係数は0.849687です。

これらの係数を使用すると、次のように近似回帰式を書くことができます。

y = 28.5986 + 0.34271(x1) – 3.00393(x2) + 0.849687(x3)

ステップ 3 (オプション): 追加の回帰統計を表示する

LINEST関数のstats引数の値をTRUEに設定して、近似回帰式の追加の回帰統計を表示することもできます。

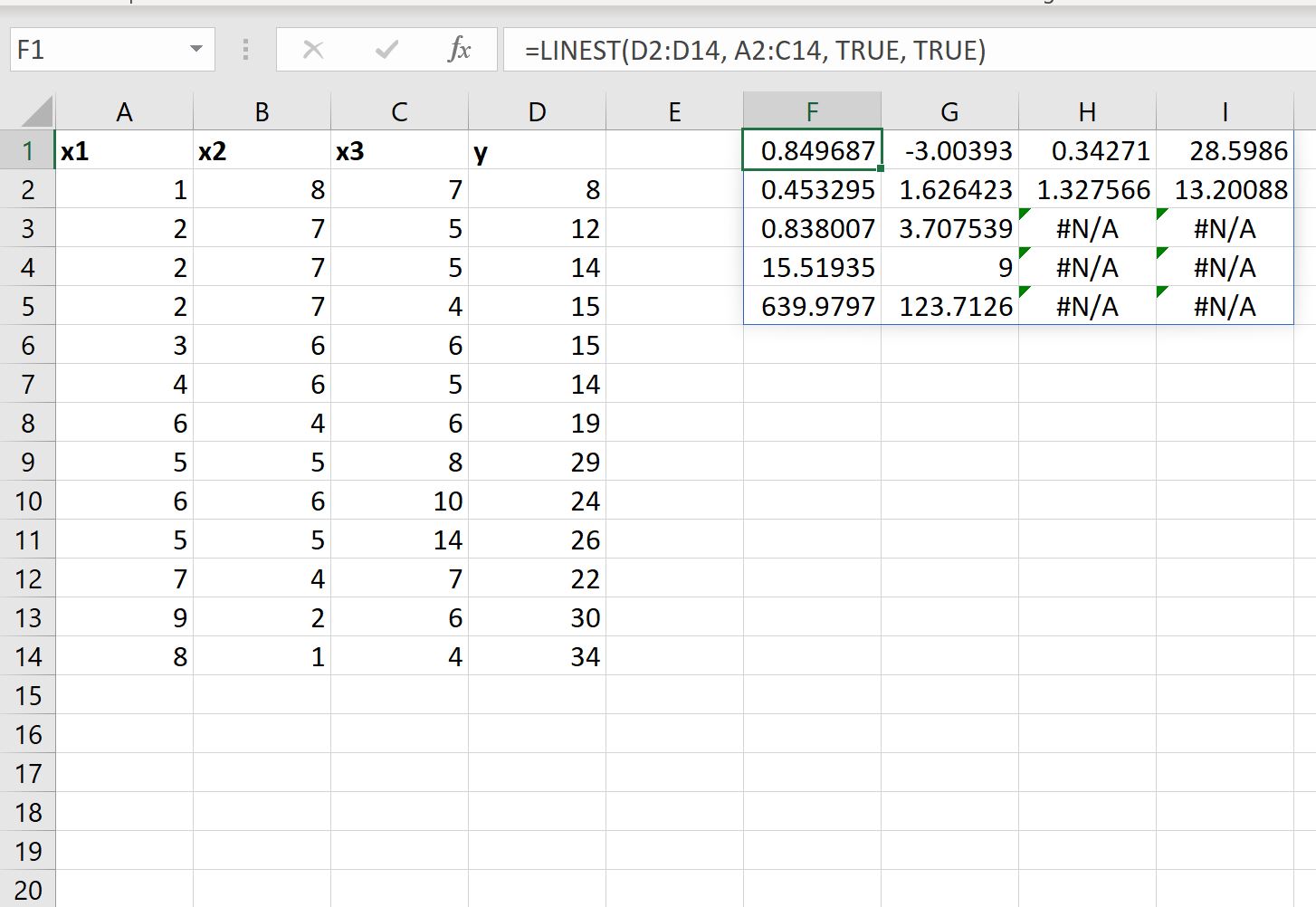
近似された回帰式は依然として同じです。

y = 28.5986 + 0.34271(x1) – 3.00393(x2) + 0.849687(x3)

結果の他の値を解釈する方法は次のとおりです。

• x3 の標準誤差は0.453295です。
• x2 の標準誤差は1.626423です。
• x1 の標準誤差は1.327566です。
• 切片の標準誤差は13.20088です。
• モデルの R ²は.838007です。
• y の残差標準誤差は3.707539です。
• 全体的な F 統計は15.51925です。
• 自由度は9です。
• 回帰平方和は639.9797です。
• 残差二乗和は123.7126です。

一般に、これらの追加統計で最も重要な尺度は R ²値です。これは、予測変数によって説明できる応答変数の分散の割合を表します。

R ²の値は 0 から 1 まで変化します。

この特定のモデルの R ^{2 は}0.838であるため、予測子変数が応答変数 y の値を適切に予測していることがわかります。

関連:適切な R 二乗値とは何ですか?

追加リソース

次のチュートリアルでは、Excel で他の一般的な操作を実行する方法について説明します。

ExcelでLOGEST関数を使う方法
Excel で非線形回帰を実行する方法
Excelで3次回帰を実行する方法