Ti-84 電卓で geometpdf() および geometcdf() を使用する方法

幾何分布は、次の特性を持つ一連の試行で最初の成功を経験する前に、一定数の失敗を経験する確率を表します。

• 考えられる結果は成功か失敗の 2 つだけです。
• 成功の確率は各試行で同じです。

確率変数X が幾何分布に従う場合、最初の成功を経験する前にk回の失敗を経験する確率は、次の式で求められます。

P(X=k) = (1-p) ^kp

金：

• k:最初の成功までの失敗回数
• p:各試行の成功確率

最初の成功までにk 回以下の失敗が発生する累積確率は、次の式を使用して求めることができます。

P(X≤k) = 1 – (1-p) ^k+1

TI-84 計算機で幾何分布にリンクされた確率を計算するには、次の関数を使用できます。

• geometpdf (確率、テスト)
• geometcdf(確率、テスト)

次の例は、これらの各関数を実際に使用する方法を示しています。

例 1: geometpdf() の使用方法

研究者が図書館の外で待っていて、人々に特定の法律を支持するかどうか尋ねたとします。特定の人が法則を支持する確率は p = 0.2 です。研究者が話しかけた 4 人目の人がその法律を最初に支持する確率はどれくらいですか?

この質問に答えるには、 geometpdf()関数を使用できます。

2nd を押してからVARSを押します。 geometpdf()までスクロールし、 ENTERを押します。

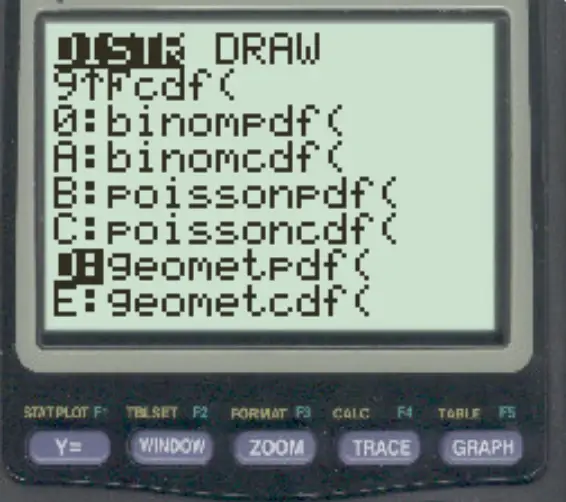
次に、次の値を入力してENTERを押します。

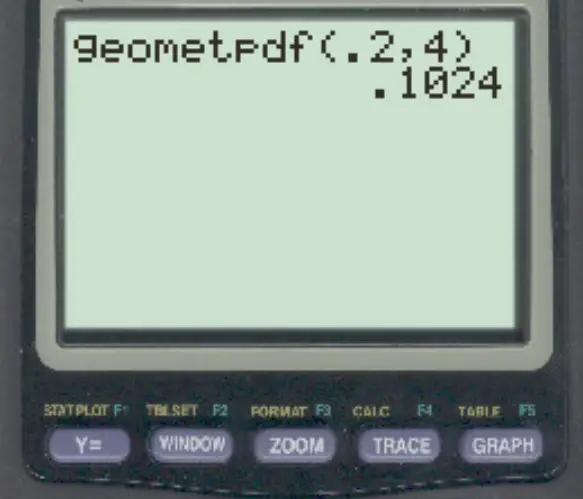
研究者が話しかけた 4 人目が最初にこの法則を支持する確率は0.1024です。

例 2: geometcdf() の使用方法

特定の銀行家を訪問する人の 4% が破産を宣告するために訪問することがわかっているとします。銀行家が破産を宣言する人に出会うまでに会う人が 9 人未満である確率はどれくらいですか?

この質問に答えるには、 geometcdf()関数を使用できます。

2nd を押してからVARSを押します。 geometcdf()まで下にスクロールし、 ENTERを押します。

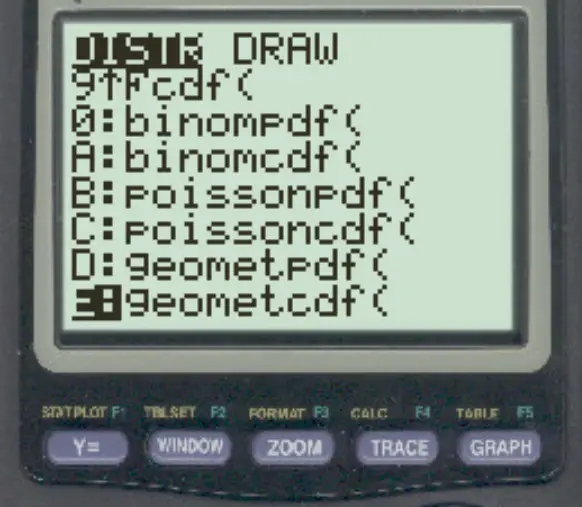
次に、次の値を入力してENTERを押します。

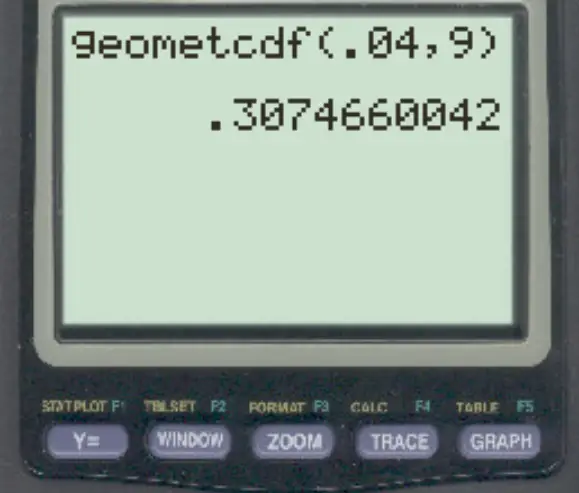
銀行家が破産を宣言する人物に出会うまでに会う人が 9 人未満である確率は0.307466です。

おまけ:このオンライン幾何分布計算ツールを自由に使用して、結果を確認してください。

追加リソース

TI-84 電卓で正規確率を計算する方法
TI-84 電卓で二項確率を計算する方法
TI-84 計算機でポアソン確率を計算する方法