Google スプレッドシートで t 検定を実行する方法

一般に、t 検定には次の 3 種類があります。

• サンプル t 検定
• 2 サンプルの T 検定
• 対応のあるサンプルの t 検定

このチュートリアルでは、Google スプレッドシートでこれらの各テストを実行する方法の例を示します。

例: 1 サンプルの t 検定

定義: 1 サンプルの t 検定は、母集団の平均が特定の値に等しいかどうかを検定するために使用されます。

例:植物学者は、特定の植物種の平均高さが 15 インチに等しいかどうかを知りたいと考えています。彼女は 12 本の植物から無作為にサンプルを採取し、それぞれの高さをインチ単位で記録しました。

次のスクリーンショットは、1 サンプルの t 検定を実行して、母集団の真の平均身長が 15 インチに等しいかどうかを判断する方法を示しています。

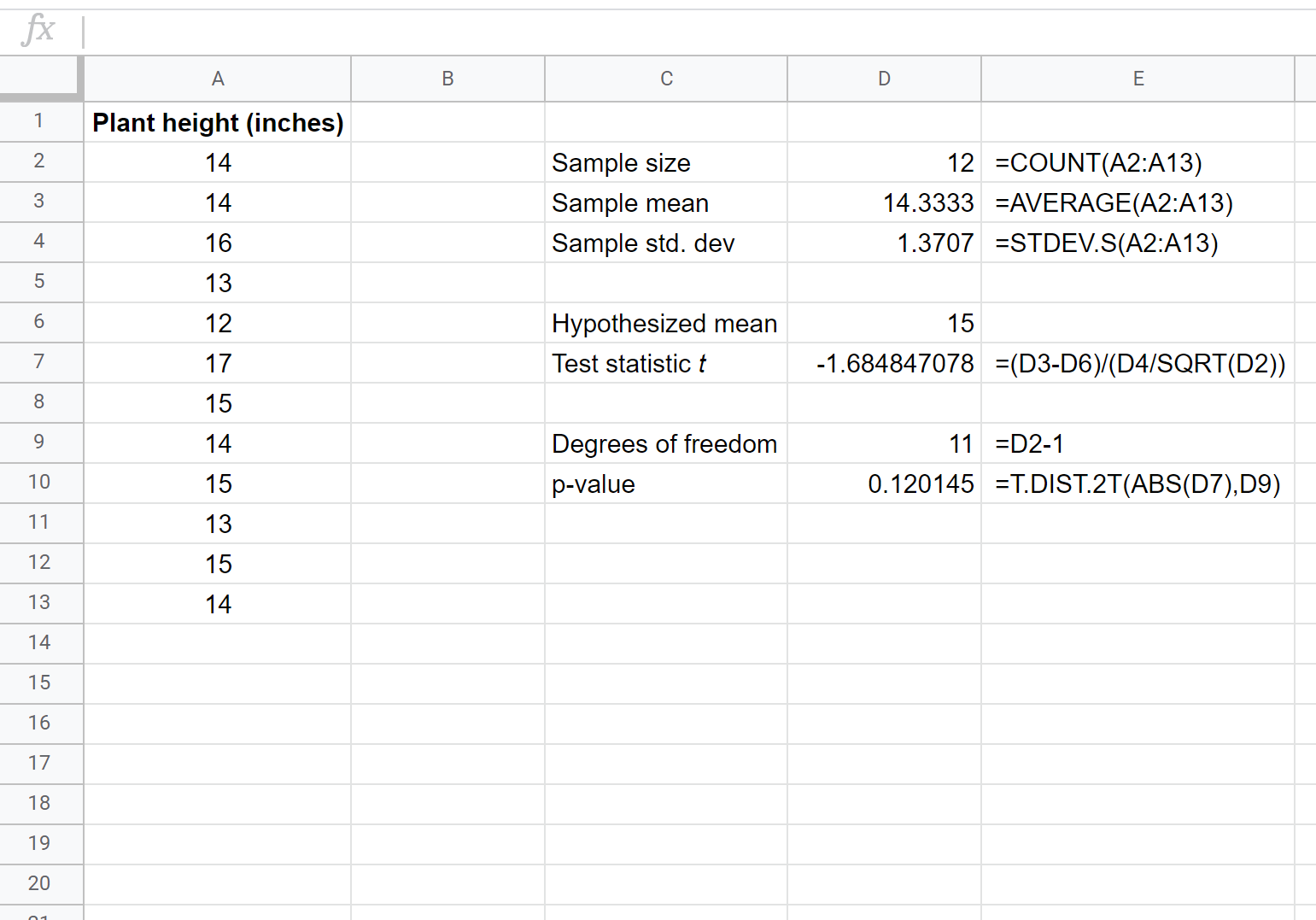
特定のサンプルに対するこの t 検定の 2 つの仮説は次のとおりです。

H ₀ : μ = 15 (この植物種の平均高さは 15 インチ)

H _A : μ ≠15 (平均身長は 15 インチではありません)

検定の p 値(0.120145)は alpha = 0.05 より大きいため、検定の帰無仮説を棄却できません。この特定の種の植物の平均高さが 15 インチ以外であると言える十分な証拠はありません。

例: 2 サンプルの t 検定

定義: 2 標本 t 検定は、 2 つの母集団の平均が等しいかどうかを検定するために使用されます。

例:研究者は、特定の国の 2 つの異なる植物種の平均高さが同じかどうかを知りたいと考えています。彼らは、各種から 20 個の植物のランダムなサンプルを収集し、各植物の高さをインチ単位で記録しました。

次のスクリーンショットは、 T.TEST()関数を使用して 2 サンプルの t 検定を実行し、2 つの母集団の平均身長が等しいかどうかを判断する方法を示しています。

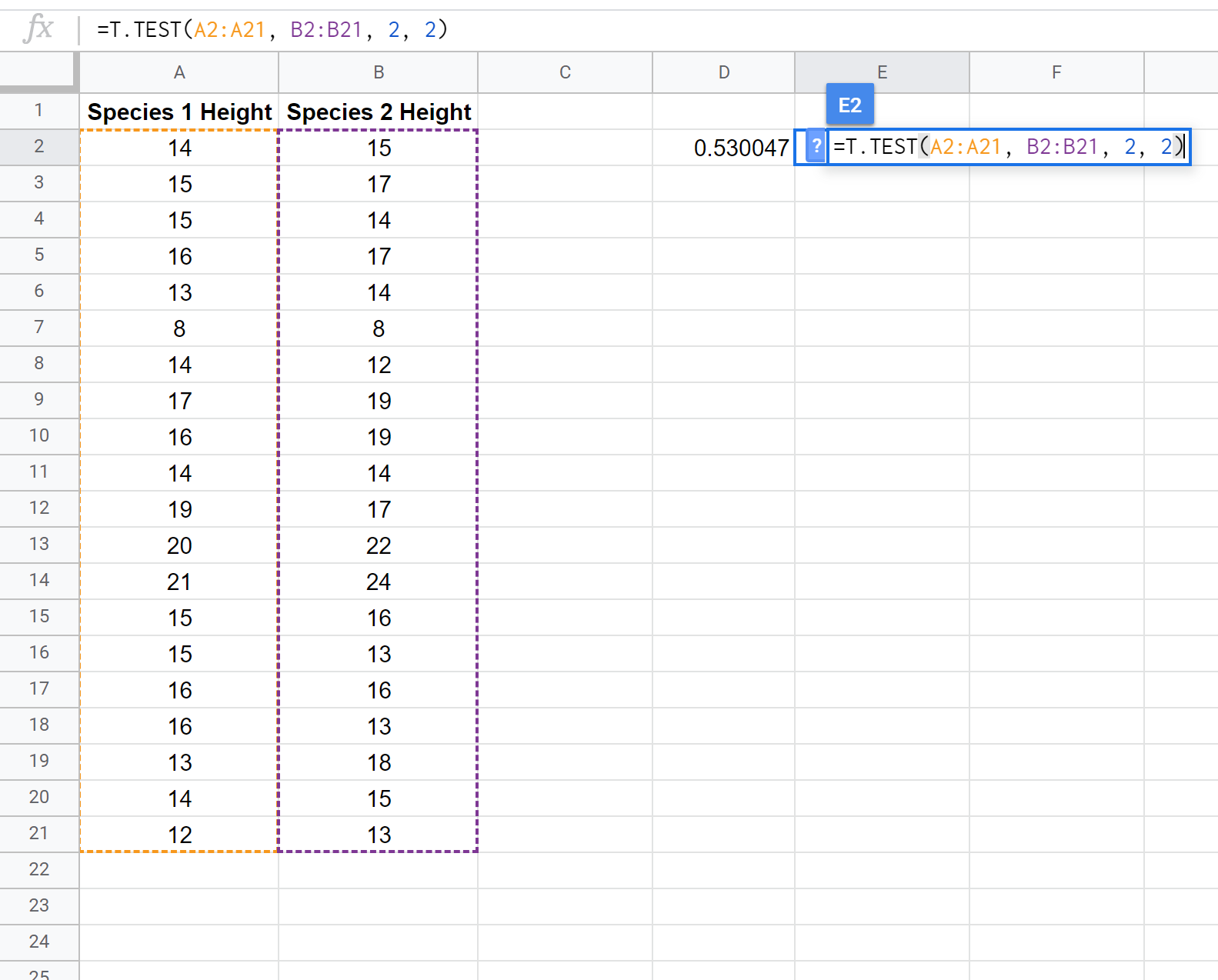
注: 2 つのサンプルの分散が同じであるという仮定の有無にかかわらず、片側 2 サンプル t 検定を実行することもできます。テストの前提条件を調整する方法については、 T.TEST ドキュメントを参照してください。

この 2 サンプル t 検定の 2 つの仮説は次のとおりです。

H ₀ : μ ₁ = μ ₂ (2 つの母集団平均は等しい)

H ₁ : μ ₁ ≠ μ ₂ (2 つの母集団平均は等しくない)

検定の p 値(0.530047)は alpha = 0.05 より大きいため、検定の帰無仮説を棄却できません。この特定の種の植物の平均高さが 15 インチ以外であると言える十分な証拠はありません。

例: 対応のあるサンプルの t 検定

定義: 対応のあるサンプルの t 検定は、一方のサンプルの各観測値がもう一方のサンプルの観測値と関連付けられる場合に、2 つのサンプルの平均を比較するために使用されます。

例:学習コースが特定の試験における生徒の成績に重大な影響を与えるかどうかを知りたいと考えています。これをテストするために、クラスの 20 人の生徒に事前テストを受けてもらいます。その後、各生徒に 2 週間のカリキュラムに参加してもらいます。その後、学生は同様の難易度のテストを再受験します。

次のスクリーンショットは、対応のあるサンプル t 検定を実行して、最初のテストと 2 番目のテストの平均スコアの差を比較する方法を示しています。

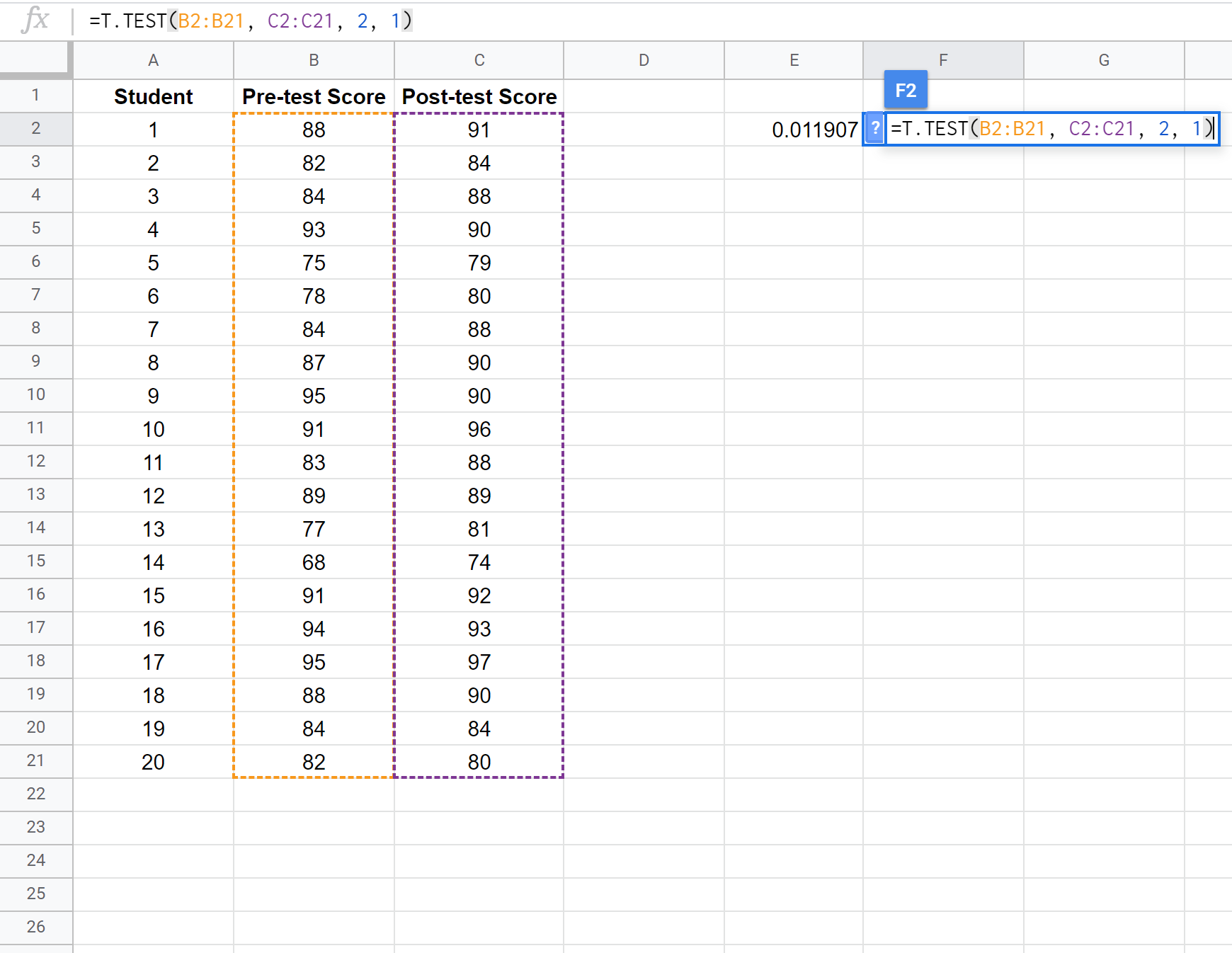
注: 2 つのサンプルの分散が同じであるという仮定の有無にかかわらず、片側 2 サンプル t 検定を実行することもできます。テストの前提条件を調整する方法については、 T.TEST ドキュメントを参照してください。

この対応のあるサンプルの t 検定の 2 つの仮定は次のとおりです。

H ₀ : μ ₁ = μ ₂ (2 つの母集団平均は等しい)

H ₁ : μ ₁ ≠ μ ₂ (2 つの母集団平均は等しくない)

検定の p 値(0.011907)は alpha = 0.05 より小さいため、検定の帰無仮説を棄却します。テスト前とテスト後の平均スコアの間に統計的に有意な差があると言える十分な証拠があります。