R での k-means クラスタリング: ステップバイステップの例

クラスタリングは、データセット内の観測値のグループを見つけようとする機械学習手法です。

目標は、各クラスター内の観測値が互いに非常に類似している一方で、異なるクラスター内の観測値が互いに大きく異なるようなクラスターを見つけることです。

クラスタリングは、 応答変数の値を予測するのではなく、単にデータセット内の構造を見つけようとしているだけであるため、 教師なし学習の一種です。

クラスタリングは、企業が次のような情報にアクセスできる場合にマーケティングでよく使用されます。

• 世帯収入
• 世帯規模
• 世帯主の職業
• 最寄りの市街地までの距離

この情報が利用可能な場合、クラスタリングを使用して、特定の製品を購入する可能性が高い、または特定の種類の広告によりよく反応する可能性が高い、類似した世帯を識別することができます。

クラスタリングの最も一般的な形式の 1 つは、 k-means クラスタリングとして知られています。

K-Means クラスタリングとは何ですか?

K 平均法クラスタリングは、データセットの各観測値をK個のクラスターの 1 つに配置する手法です。

最終的な目標は、各クラスター内の観測値が互いによく似ている一方で、異なるクラスター内の観測値が互いにまったく異なるK個のクラスターを作成することです。

実際には、次の手順を使用して K-means クラスタリングを実行します。

1. Kの値を選択します。

• まず、データ内で識別するクラスターの数を決定する必要があります。多くの場合、 Kのいくつかの異なる値をテストし、その結果を分析して、特定の問題に対してどのクラスターの数が最も合理的であるかを確認する必要があります。

2. 各観測値を 1 からKまでの初期クラスターにランダムに割り当てます。

3. クラスターの割り当てが変更されなくなるまで、次の手順を実行します。

• K個のクラスターのそれぞれについて、クラスターの重心を計算します。これは単に、 k 番目のクラスターの観測値のp平均特徴のベクトルです。
• 各観測値を最も近い重心を持つクラスターに割り当てます。ここで、最も近いはユークリッド距離を使用して定義されます。

R での K-Means クラスタリング

次のチュートリアルでは、R で K-means クラスタリングを実行する方法の段階的な例を示します。

ステップ 1: 必要なパッケージをロードする

まず、R の K-means クラスタリングに役立ついくつかの関数を含む 2 つのパッケージを読み込みます。

 library (factoextra)
library (cluster)

ステップ 2: データのロードと準備

この例では、R に組み込まれているUSArrestsデータセットを使用します。このデータセットには、1973 年の米国各州の人口 100,000 人あたりの殺人、暴行、強姦の逮捕数と、都市部に住む各州の人口の割合が含まれています。地域。 、アーバンポップ。

次のコードは、次のことを行う方法を示しています。

• USArrestsデータセットをロードする
• 欠損値のある行をすべて削除します
• データセット内の各変数を、平均が 0、標準偏差が 1 になるようにスケーリングします。

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

ステップ 3: 最適なクラスター数を見つける

R で K 平均法クラスタリングを実行するには、次の構文を使用する組み込みkmeans()関数を使用できます。

kmeans (データ、センター、nstart)

金：

• data:データセットの名前。
• centers:クラスターの数 ( kで示されます)。
• nstart:初期設定の数。初期開始クラスターが異なると異なる結果が生じる可能性があるため、いくつかの異なる初期構成を使用することをお勧めします。 K 平均法アルゴリズムは、クラスター内で最小の変動をもたらす初期構成を見つけます。

最適なクラスターの数が事前にわからないため、決定に役立つ 2 つの異なるグラフを作成します。

1. 平方和の合計に対するクラスターの数

まず、 fviz_nbclust()関数を使用して、クラスター数と平方和の合計のプロットを作成します。

 fviz_nbclust(df, kmeans, method = “ wss ”) 

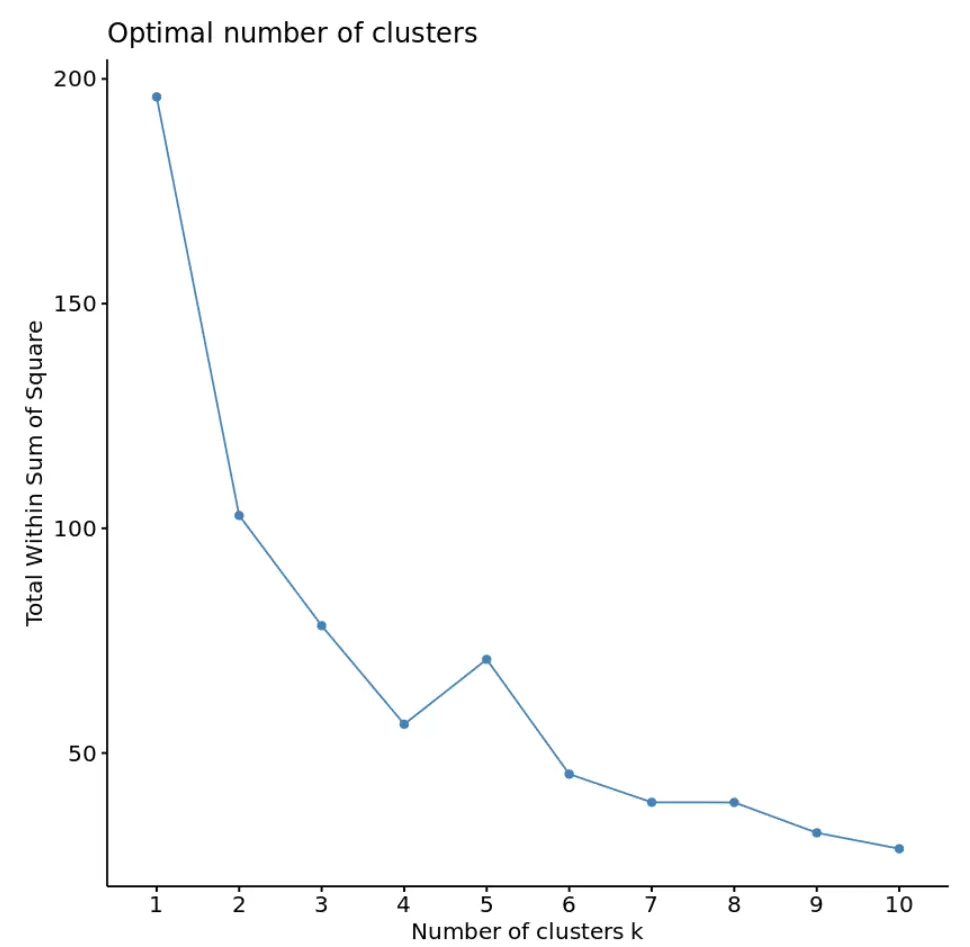
通常、このタイプのプロットを作成するときは、平方和が「曲がる」か横ばいになり始める「膝」を探します。これは通常、最適なクラスター数です。

このグラフでは、k = 4 クラスターに小さなねじれまたは「曲がり」があるように見えます。

2. クラスター数とギャップ統計

最適なクラスター数を決定するもう 1 つの方法は、 偏差統計と呼ばれるメトリックを使用することです。これは、k のさまざまな値のクラスター内変動の合計を、クラスター化を行わない分布の期待値と比較します。

クラスターパッケージのclusGap()関数を使用してクラスターの各数のギャップ統計を計算したり、 fviz_gap_stat()関数を使用してギャップ統計に対してクラスターをプロットしたりできます。

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

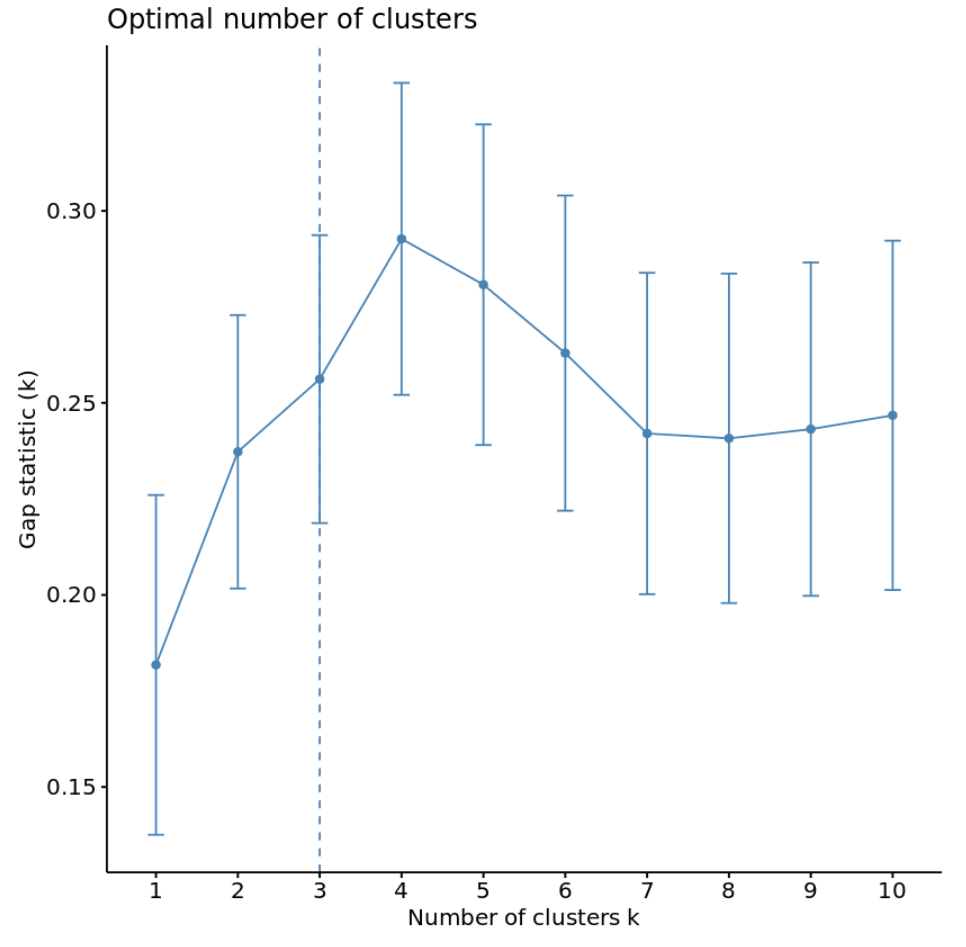
グラフから、ギャップ統計が k = 4 クラスターで最も高くなることがわかります。これは、以前に使用したエルボー法に対応します。

ステップ 4: 最適なKを使用して K-Means クラスタリングを実行する

最後に、 kの最適値 4 を使用して、データセットに対して k-means クラスタリングを実行できます。

 #make this example reproducible
set.seed(1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

結果から次のことがわかります。

• 16 の状態が最初のクラスターに割り当てられました
• 13 の状態が 2 番目のクラスターに割り当てられています
• 13 の州が 3 番目のクラスターに割り当てられています
• 8 つの状態が 4 番目のクラスターに割り当てられています

fivz_cluster()関数を使用して、軸上の最初の 2 つの主成分を表示する散布図でクラスターを視覚化できます。

 #plot results of final k-means model
fviz_cluster(km, data = df)

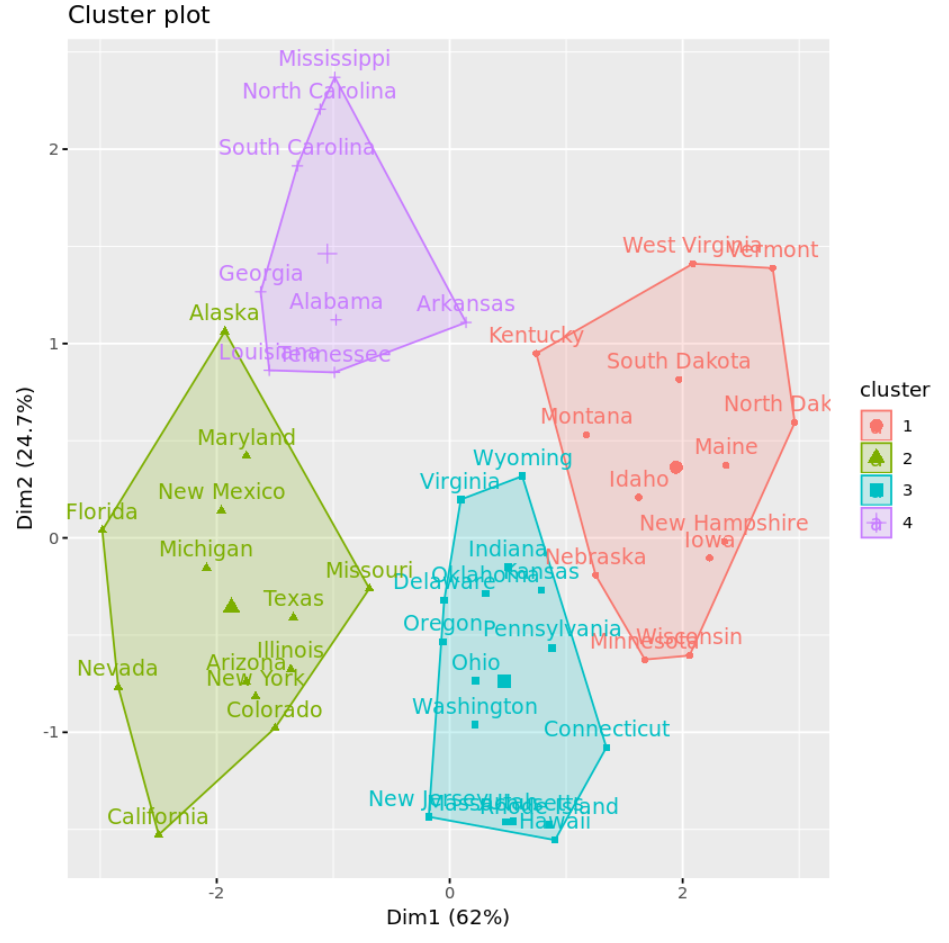
Aggregate()関数を使用して、各クラスター内の変数の平均を見つけることもできます。

 #find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)

cluster Murder Assault UrbanPop Rape
				
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250

この出力を次のように解釈します。

• グループ 1 の州の国民 10 万人当たりの平均殺人件数は3.6 件です。
• グループ 1 の州の国民 10 万人当たりの平均暴行件数は78.5 件です。
• グループ 1 の州の都市部に住んでいる住民の平均割合は52.1%です。
• グループ 1 の州の国民 10 万人当たりの平均強姦件数は12.2 件です。

等々。

各州のクラスター割り当てを元のデータセットに追加することもできます。

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

K-Means クラスタリングの長所と短所

K-means クラスタリングには次の利点があります。

• 高速なアルゴリズムです。
• 大規模なデータセットを適切に処理できます。

ただし、次のような潜在的な欠点があります。

• これには、アルゴリズムを実行する前にクラスターの数を指定する必要があります。
• 異常値には敏感です。

K 平均法クラスタリングに代わる 2 つの方法は、 K 平均法クラスタリングと階層的クラスタリングです。

この例で使用されている完全な R コードは、 ここで見つけることができます。