Python で ols 回帰を実行する方法 (例あり)
通常最小二乗 (OLS) 回帰は、1 つ以上の予測子変数と応答変数の間の関係を最もよく表す直線を見つけることを可能にする方法です。
この方法により、次の方程式を見つけることができます。
ŷ = b 0 + b 1 x
金:
- ŷ : 推定応答値
- b 0 : 回帰直線の原点
- b 1 : 回帰直線の傾き
この方程式は、予測子と応答変数の関係を理解するのに役立ち、予測子変数の値に基づいて応答変数の値を予測するために使用できます。
次のステップバイステップの例は、Python で OLS 回帰を実行する方法を示しています。
ステップ 1: データを作成する
この例では、15 人の生徒に対して次の 2 つの変数を含むデータセットを作成します。
- 総学習時間数
- 試験の結果
時間を予測変数として、試験スコアを応答変数として使用して、OLS 回帰を実行します。
次のコードは、パンダでこの偽のデータセットを作成する方法を示しています。
import pandas as pd #createDataFrame df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14], ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]}) #view DataFrame print (df) hours score 0 1 64 1 2 66 2 4 76 3 5 73 4 5 74 5 6 81 6 6 83 7 7 82 8 8 80 9 10 88 10 11 84 11 11 82 12 12 91 13 12 93 14 14 89
ステップ 2: OLS 回帰を実行する
次に、 statsmodelsモジュールの関数を使用して、予測変数として時間を使用し、応答変数としてスコアを使用して OLS 回帰を実行できます。
import statsmodels.api as sm
#define predictor and response variables
y = df[' score ']
x = df[' hours ']
#add constant to predictor variables
x = sm. add_constant (x)
#fit linear regression model
model = sm. OLS (y,x). fit ()
#view model summary
print ( model.summary ())
OLS Regression Results
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1
Covariance Type: non-robust
==================================================== ============================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================
coef列から回帰係数を確認し、次の近似回帰式を書くことができます。
スコア = 65.334 + 1.9824*(時間)
これは、学習時間が追加されるごとに、試験の平均スコアが1.9824ポイント増加することを意味します。
元の値65,334 は、 0 時間勉強した生徒の予想される試験の平均スコアを示しています。
この方程式を使用して、学生の勉強時間に基づいて予想される試験の得点を求めることもできます。
たとえば、10 時間勉強した学生は、試験スコア85.158を達成する必要があります。
スコア = 65.334 + 1.9824*(10) = 85.158
モデルの概要の残りの部分を解釈する方法は次のとおりです。
- P(>|t|):これはモデル係数に関連付けられた p 値です。時間の p 値 (0.000) は 0.05 未満であるため、時間とスコアの間に統計的に有意な関連があると言えます。
- R 二乗:これは、試験の得点の変動のパーセンテージが勉強時間数によって説明できることを示しています。この場合、スコアの変動の83.1%は勉強時間によって説明できます。
- F 統計量と p 値: F 統計量 ( 63.91 ) と対応する p 値 ( 2.25e-06 ) は、回帰モデルの全体的な有意性、つまりモデル内の予測子変数が変動の説明に役立つかどうかを示します。応答変数に。この例の p 値は 0.05 未満であるため、モデルは統計的に有意であり、時間はスコアの変動を説明するのに役立つと考えられます。
ステップ 3: 最適なラインを視覚化する
最後に、 matplotlibデータ視覚化パッケージを使用して、実際のデータ ポイントに適合した回帰直線を視覚化できます。
import matplotlib. pyplot as plt
#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )
#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')
#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)
#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )
#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')
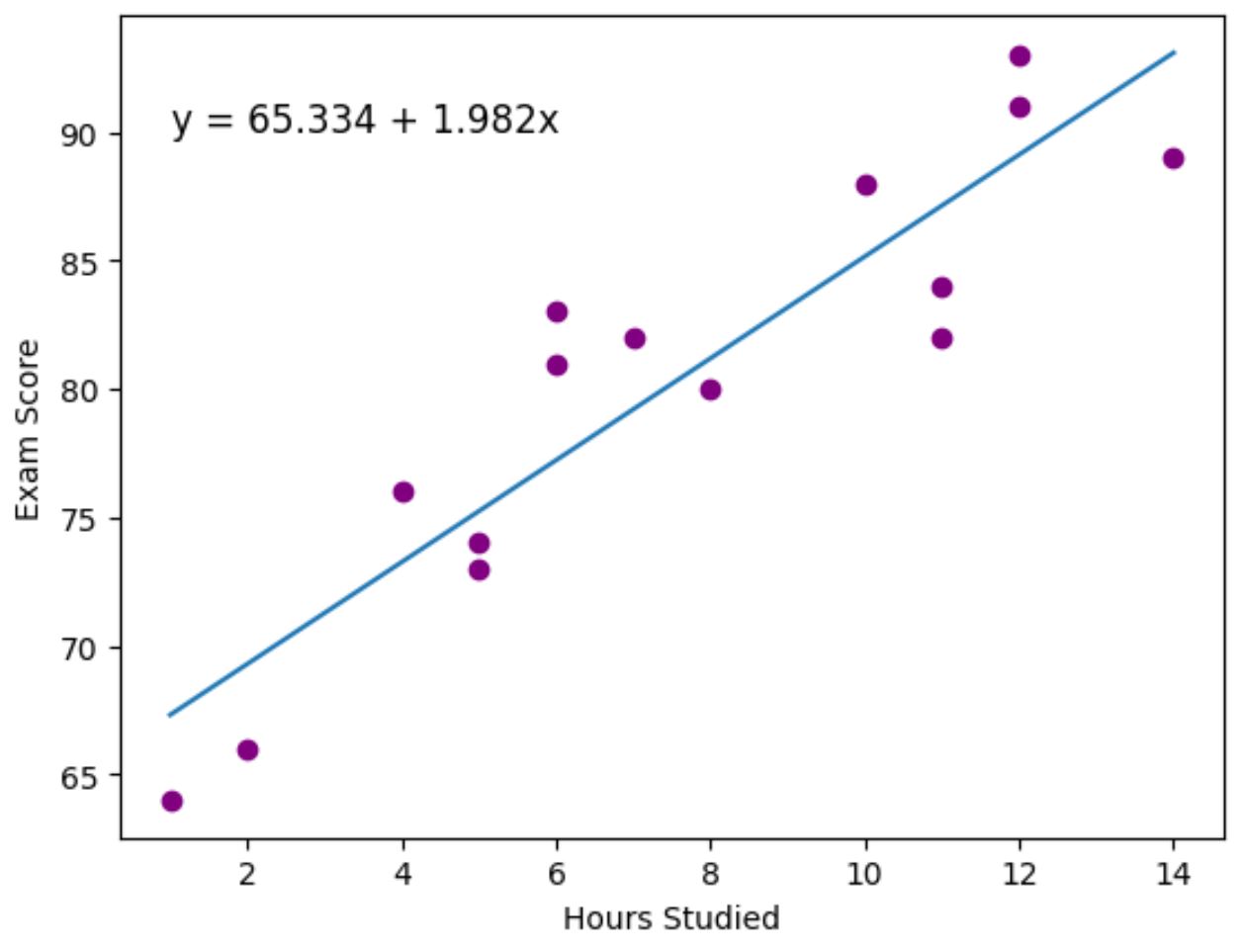
紫色の点は実際のデータ ポイントを表し、青色の線は近似された回帰直線を表します。
また、 plt.text()関数を使用して、近似回帰式をプロットの左上隅に追加しました。
グラフを見ると、近似回帰直線が時間変数とスコア変数の間の関係を非常によく捉えていることがわかります。
追加リソース
次のチュートリアルでは、Python で他の一般的なタスクを実行する方法について説明します。
Python でロジスティック回帰を実行する方法
Python で指数回帰を実行する方法
Python で回帰モデルの AIC を計算する方法