統計における確率質量関数 (pmf) とは何ですか?

確率質量関数(PMF)は、離散確率変数が特定の値を取る確率を示します。

たとえば、サイコロを 1 回振ったとします。サイコロが出る数字を x とすると、 xが異なる値に等しい確率は次のように説明できます。

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

サイコロが 1 から 6 までのいずれかの数字に当たる確率は等しいです。

これらの確率を確率質量関数として記述する方法は次のとおりです。

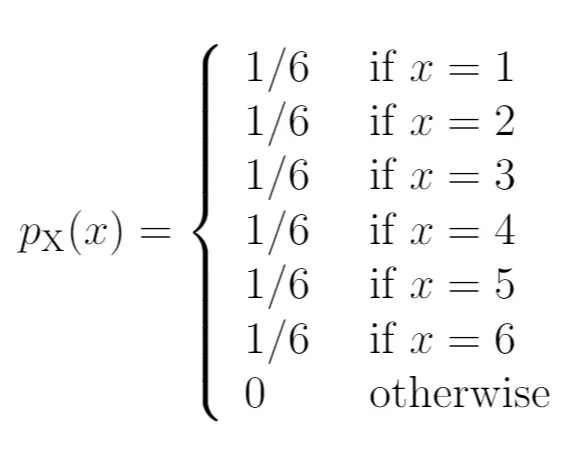
図の左側は、右側の結果に関連する確率を示しています。

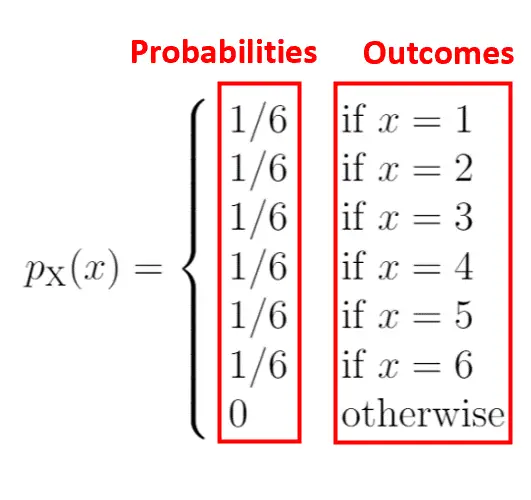
確率質量関数の特性は、すべての確率の合計が 1 にならなければならないことです。この PMF が次の条件を満たしていることがわかります。

確率の合計 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1。

確率質量関数のサポートとは、離散確率変数が取り得る値のセットを指します。この例では、サイコロの値はこれらの値のいずれかを取れるため、サポートは {1, 2, 3, 4, 5, 6} になります。

サポート外の場合、PMF 値はゼロです。たとえば、サイコロが「0」、「7」、または「8」に当たる確率は、これらの数字が括弧内に含まれていないため、ゼロになります。

実際の確率質量関数

実際に確率質量関数の最も一般的な 2 つの例は、二項分布とポアソン分布に関するものです。

二項分布

確率変数X が二項分布に従う場合、 X = kが成功する確率は次の式で求められます。

P(X=k) = _n C _k * p ^k * (1-p) ^nk

金：

• n:試行回数
• k:成功回数
• p:与えられた試行の成功確率
• _n C _k : n回の試行でk 個の成功を得る方法の数

たとえば、コインを3回投げたとします。上記の式を使用して、これら 3 回のトスで 0、1、2、および 3 の表が出る確率を決定できます。

• P(X=0) = ₃ C ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125
• P(X=1) = ₃ C ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 1 * 1 * (0.5) ² = 0.375
• P(X=2) = ₃ C ₂ * 0.5 ² * (1-0.5) ^3-2 = 1 * 1 * (0.5) ¹ = 0.375
• P(X=3) = ₃ C ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 1 * (0.5) ⁰ = 0.125

魚の分布

確率変数X がポアソン分布に従う場合、 X = kが成功する確率は次の式で求められます。

P(X=k) = λ ^k * e ^{– λ} / k!

金：

• λ:特定の間隔中に発生した成功の平均数
• k:成功回数
• e:約 2.71828 に等しい定数

たとえば、特定の病院で 1 時間あたり平均 2 件の出産があったとします。上記の式を使用して、0、1、2、3 回の出産などを経験する確率を決定できます。特定の時間内に:

• P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0.1353
• P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0.2707
• P(X=2) = 2 ² * e ^{– 2} / 2! = 0.2707
• P(X=3) = 2 ³ * e ^{– 2} / 3! = 0.1805

PMF を見る

私たちは確率質量関数を棒グラフで視覚化することがよくあります。

たとえば、次の棒グラフは、前の例で説明したポアソン分布の 1 時間あたりの出生数に関連する確率を示しています。

出生数は無限大にまで伸びる可能性がありますが、10 を超えると確率が非常に小さくなり、棒グラフでさえ見ることができないことに注意してください。

PMF のプロパティ

確率質量関数には次の特性があります。

1. すべての確率はサポートにおいてプラスです。たとえば、サイコロが 1 と 6 の間に当たる確率は正ですが、他のすべての結果の確率はゼロです。

2. すべての結果の確率は 0 から 1 の間です。たとえば、サイコロが 1 から 6 の間に当たる確率は 1/6、つまり各結果について 0.1666666 です。

3. すべての確率の合計は 1 に等しくなければなりません。たとえば、特定の数字に当たるサイコロの確率の合計は、1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1 です。 /6 = 1。

追加リソース

確率変数とは何ですか?
CDF と PDF: 違いは何ですか?
二項分布の概要
ポアソン分布の概要