Python でチャウテストを実行する方法
チャウ検定は、異なるデータセット上の 2 つの異なる回帰モデルの係数が等しいかどうかをテストするために使用されます。
このテストは通常、時系列データを使用した計量経済学の分野で、特定の時点でデータに構造的な断絶があるかどうかを判断するために使用されます。
次のステップバイステップの例は、Python で Chow テストを実行する方法を示しています。
ステップ 1: データを作成する
まず、偽のデータを作成します。
import pandas as pd #createDataFrame df = pd. DataFrame ({' x ': [1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10, 10, 11, 12, 12, 13, 14, 15, 15, 16, 17, 18, 18, 19, 20, 20], ' y ': [3, 5, 6, 10, 13, 15, 17, 14, 20, 23, 25, 27, 30, 30, 31, 33, 32, 32, 30, 32, 34, 34, 37, 35, 34, 36, 34, 37, 38, 36]}) #view first five rows of DataFrame df. head () x y 0 1 3 1 1 5 2 2 6 3 3 10 4 4 13
ステップ 2: データを視覚化する
次に、データを視覚化するための単純な散布図を作成します。
import matplotlib. pyplot as plt
#create scatterplot
plt. plot (df. x , df. y , ' o ')
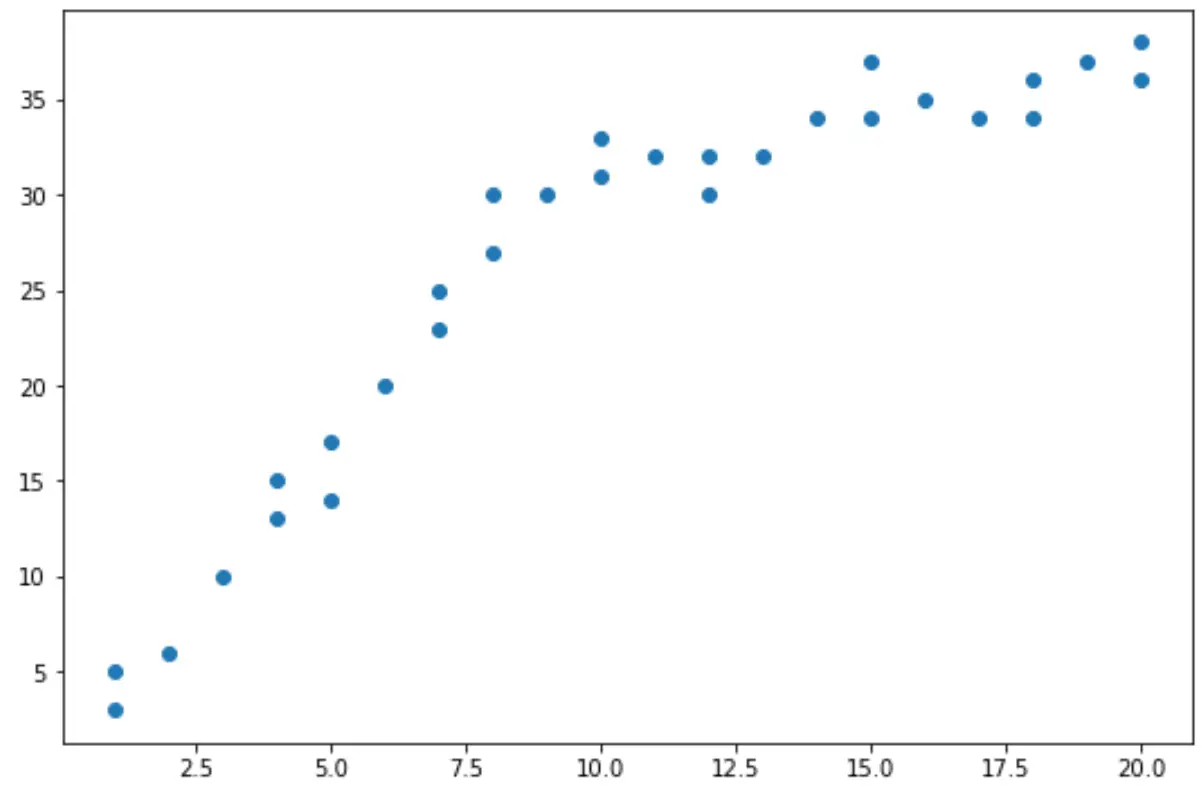
散布図から、データの傾向が x = 10 で変化しているように見えることがわかります。
したがって、Chow テストを実行して、x = 10 のデータに構造的ブレークポイントがあるかどうかを判断できます。
ステップ 3: 食事テストを実行する
Python のchowtestパッケージの chowtest 関数を使用して、Chow テストを実行できます。
まず、pip を使用してこのパッケージをインストールする必要があります。
pip install chowtest
次に、次の構文を使用して Chow テストを実行できます。
from chow_test import chowtest chowtest ( y=df[[' y ']], last_index_in_model_1= 15 , first_index_in_model_2= 16 , significance_level= .05 ) ************************************************** ********************************* Reject the null hypothesis of equality of regression coefficients in the 2 periods. ************************************************** ********************************* Chow Statistic: 118.14097335479373 p value: 0.0 ************************************************** ********************************* (118.14097335479373, 1.1102230246251565e-16)
chowtest()関数の個々の引数の意味は次のとおりです。
- y : DataFrame 内の応答変数
- x : DataFrame 内の予測変数
- last_index_in_model_1 : 構造的ブレークの前の最後のポイントのインデックス値
- first_index_in_model_2 : 構造破壊後の最初のポイントのインデックス値
- Significance_level : 仮説検定に使用する有意水準
テスト結果から次のことがわかります。
- F 検定統計量: 118.14
- p値: <.0000
p 値は 0.05 未満であるため、検定の帰無仮説を棄却できます。これは、データ内に構造的ブレークポイントが存在すると言える十分な証拠があることを意味します。
言い換えれば、2 つの回帰直線は 1 つの回帰直線よりも効果的にデータにモデルを当てはめることができます。
追加リソース
次のチュートリアルでは、Python で他の一般的なテストを実行する方法について説明します。
Python でグレンジャー因果関係テストを実行する方法
Python で Breusch-Pagan テストを実行する方法
Python で White のテストを実行する方法