Python で正規性をテストする方法 (4 つの方法)
多くの統計テストは、データセットが正規分布していることを前提としています。
Python でこの仮説を確認するには、次の 4 つの一般的な方法があります。
1. (視覚的方法) ヒストグラムを作成します。
- ヒストグラムがほぼ「ベル」型の場合、データは正規分布していると見なされます。
2. (視覚的方法) QQ プロットを作成します。
- プロット上の点がほぼ直線の対角線に沿って配置されている場合、データは正規分布しているとみなされます。
3. (正式な統計検定) Shapiro-Wilk 検定を実行します。
- 検定の p 値が α = 0.05 より大きい場合、データは正規分布しているとみなされます。
4. (正式な統計検定) コルモゴロフ・スミルノフ検定を実行します。
- 検定の p 値が α = 0.05 より大きい場合、データは正規分布しているとみなされます。
次の例は、これらの各メソッドを実際に使用する方法を示しています。
方法 1: ヒストグラムを作成する
次のコードは、 対数正規分布に従うデータ セットのヒストグラムを作成する方法を示しています。
import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt
#make this example reproducible
n.p. random . seeds (1)
#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)
#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20)
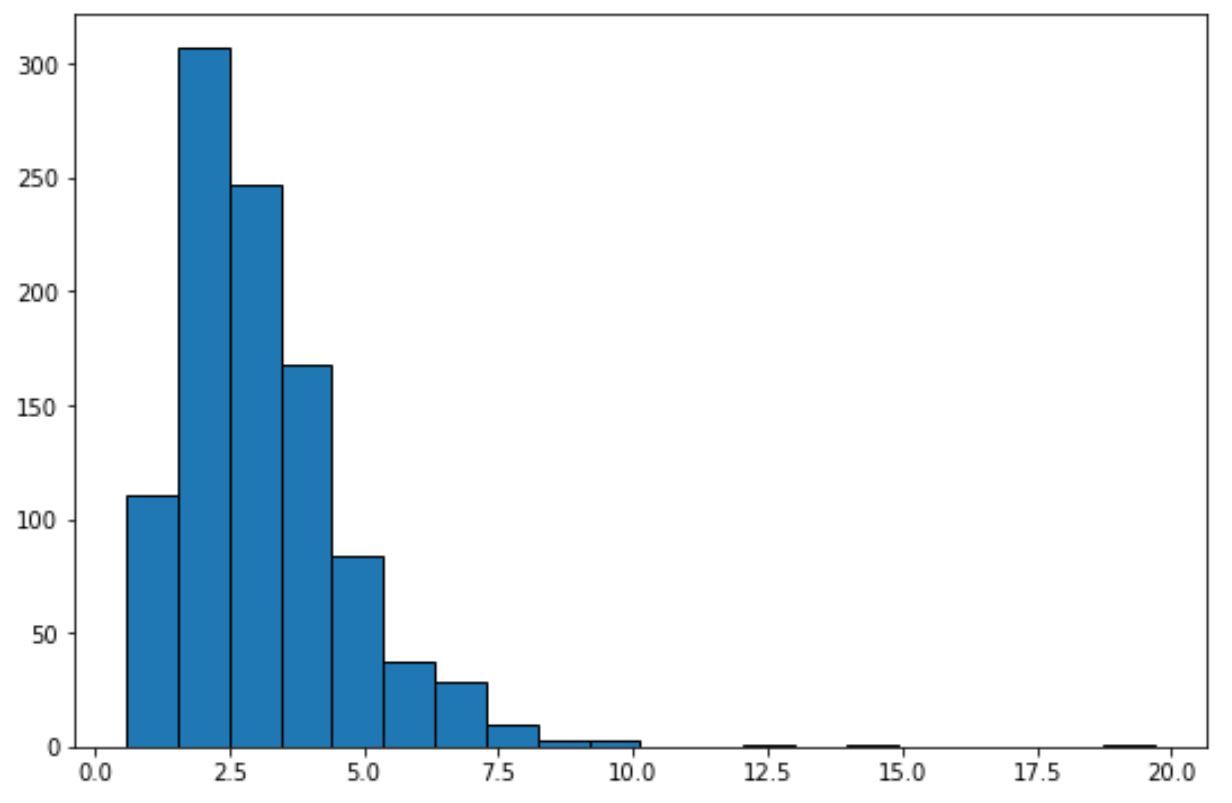
このヒストグラムを見るだけで、データセットが「釣鐘型」を示しておらず、正規分布していないことがわかります。
方法 2: QQ プロットを作成する
次のコードは、対数正規分布に従うデータ セットの QQ プロットを作成する方法を示しています。
import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt
#make this example reproducible
n.p. random . seeds (1)
#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)
#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')
plt. show ()
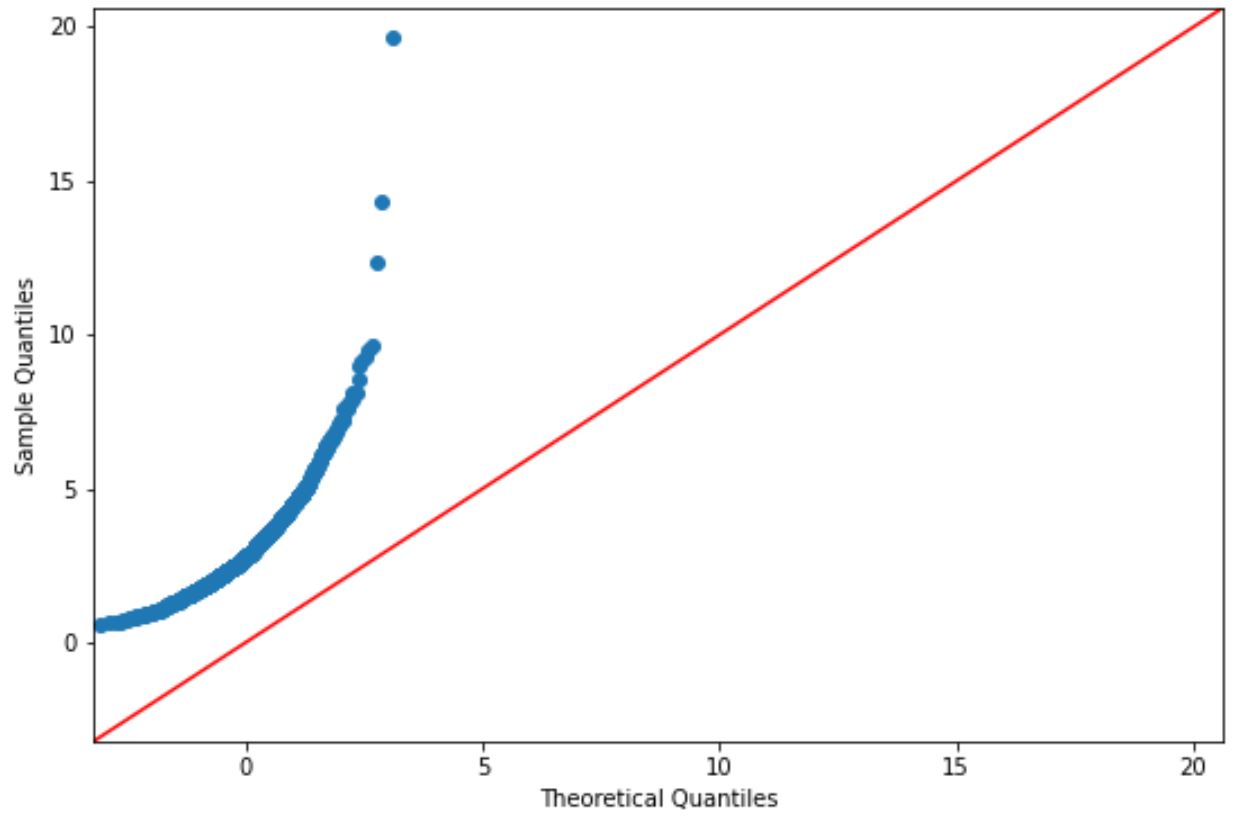
プロット ポイントが直線の対角線にほぼ沿って配置されている場合、通常、データ セットは正規分布していると想定されます。
ただし、このグラフ上の点は明らかに赤い線に対応していないため、このデータセットが正規分布していると仮定することはできません。
対数正規分布関数を使用してデータを生成したことを考えると、これは当然のことです。
方法 3: シャピロ-ウィルク テストを実行する
次のコードは、対数正規分布に従うデータ セットに対して Shapiro-Wilk を実行する方法を示しています。
import math
import numpy as np
from scipy.stats import shapiro
from scipy. stats import lognorm
#make this example reproducible
n.p. random . seeds (1)
#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)
#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)
ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)
結果から、検定統計量は0.857で、対応する p 値は3.88e-29 (ゼロに非常に近い) であることがわかります。
p 値が 0.05 未満であるため、Shapiro-Wilk 検定の帰無仮説を棄却します。
これは、標本データが正規分布からのものではないことを示す十分な証拠があることを意味します。
方法 4: コルモゴロフ・スミルノフ検定を実行する
次のコードは、対数正規分布に従うデータ セットに対してコルモゴロフ-スミルノフ検定を実行する方法を示しています。
import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm
#make this example reproducible
n.p. random . seeds (1)
#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)
#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')
KstestResult(statistic=0.84125708308077, pvalue=0.0)
結果から、検定統計量は0.841で、対応する p 値は0.0であることがわかります。
p 値が 0.05 未満であるため、コルモゴロフ-スミルノフ検定の帰無仮説を棄却します。
これは、標本データが正規分布からのものではないことを示す十分な証拠があることを意味します。
非正規データの扱い方
特定のデータセットが正規分布していない場合、多くの場合、次のいずれかの変換を実行して、より正規分布にすることができます。
1. 対数変換: x の値をlog(x)に変換します。
2. 平方根変換: x の値を√xに変換します。
3. 立方根変換: x の値をx 1/3に変換します。
これらの変換を実行すると、データセットは通常、より正規分布になります。
Python でこれらの変換を実行する方法については、 このチュートリアルを読んでください。