Python で正規 cdf を計算してプロットする方法
累積分布関数 ( CDF ) は、確率変数が特定の値以下の値を取る確率を示します。
このチュートリアルでは、Python で正規 CDF 値を計算してプロットする方法を説明します。
例 1: Python で正規 CDF 確率を計算する
Python で正規 CDF 確率を計算する最も簡単な方法は、 SciPyライブラリのNorm.cdf()関数を使用することです。
次のコードは、標準正規分布で確率変数が 1.96 未満の値を取る確率を計算する方法を示しています。
from scipy. stats import norm #calculate probability that random value is less than 1.96 in normal CDF norm. cdf ( 1.96 ) 0.9750021048517795
標準正規分布で確率変数が 1.96 未満の値をとる確率は約0.975です。
また、この値を 1 から引くだけで、確率変数が 1.96 より大きい値を取る確率を求めることもできます。
from scipy. stats import norm #calculate probability that random value is greater than 1.96 in normal CDF 1 - norm. cdf ( 1.96 ) 0.024997895148220484
標準正規分布で確率変数が 1.96 より大きい値を取る確率は約0.025です。
例 2: 標準 CDF のプロット
次のコードは、Python で通常の CDF をプロットする方法を示しています。
import matplotlib. pyplot as plt import numpy as np import scipy. stats as ss #define x and y values to use for CDF x = np. linspace (-4, 4, 1000) y = ss. norm . cdf (x) #normal plot CDF plt. plot (x, y)
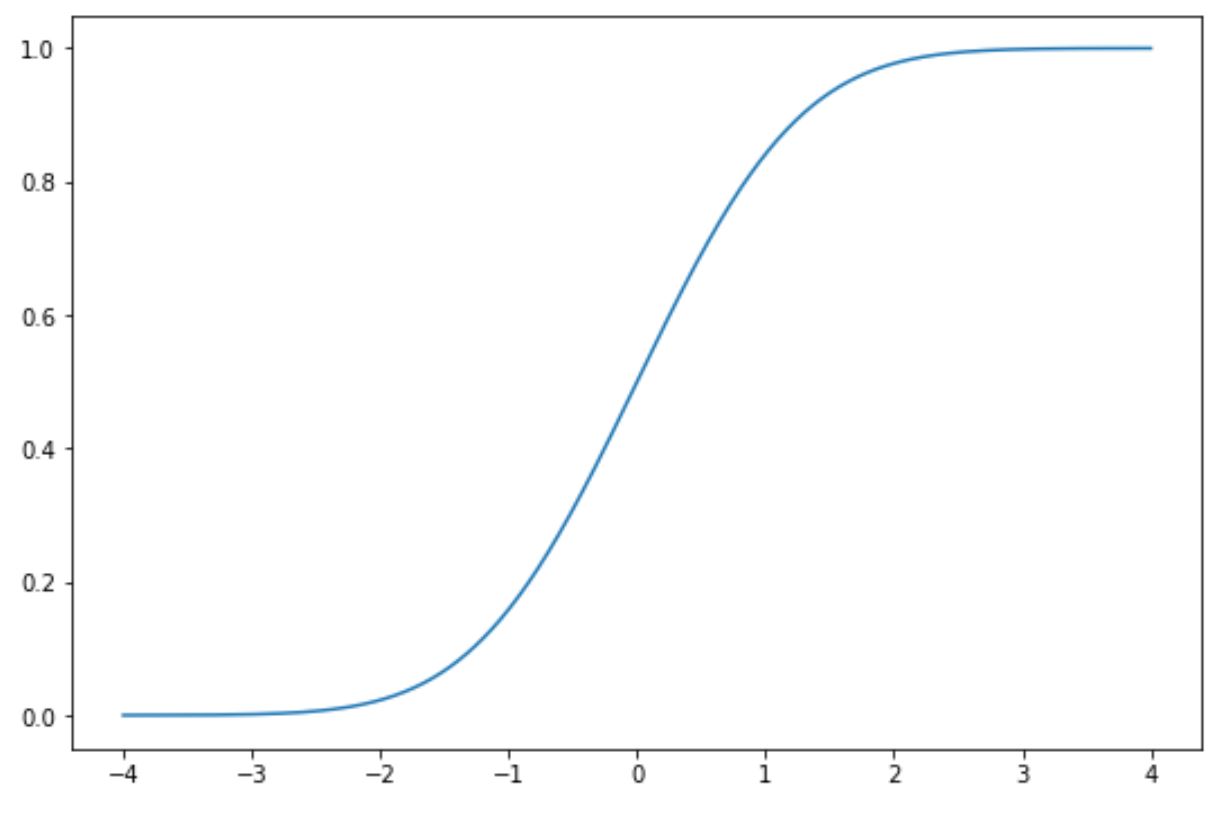
x 軸は標準正規分布に従う確率変数の値を示し、y 軸は確率変数が x 軸に示された値よりも小さい値を取る確率を示します。
たとえば、x = 1.96 に注目すると、x が 1.96 未満である累積確率は約0.975であることがわかります。
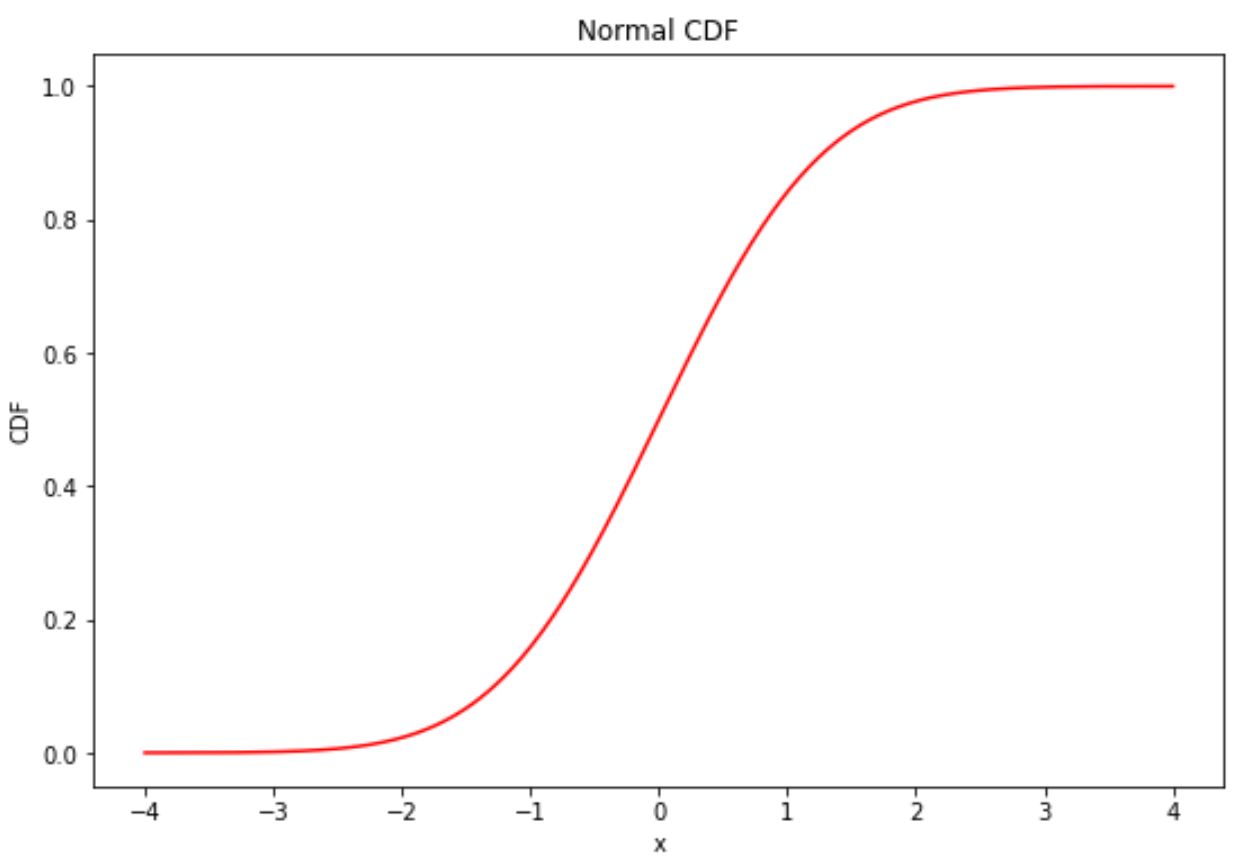
通常の CDF プロットの軸の色とラベルも自由に変更できます。
import matplotlib. pyplot as plt import numpy as np import scipy. stats as ss #define x and y values to use for CDF x = np. linspace (-4, 4, 1000) y = ss. norm . cdf (x) #normal plot CDF plt. plot (x,y,color=' red ') plt. title (' Normal CDF ') plt. xlabel (' x ') plt. ylabel (' CDF ')
追加リソース
次のチュートリアルでは、Python で他の一般的な操作を実行する方法について説明します。