Python で二変量分析を実行する方法: 例付き
二変量分析という用語は、2 つの変数の分析を指します。接頭辞「bi」は「2」を意味するので、これを覚えておくとよいでしょう。
二変量解析の目標は、2 つの変数間の関係を理解することです。
二変量解析を実行するには、次の 3 つの一般的な方法があります。
1.点群
2.相関係数
3.単純な線形回帰
次の例は、2 つの変数に関する情報を含む次の pandas DataFrame を使用して、Python でこれらのタイプの二変量分析を実行する方法を示しています: (1)勉強に費やした時間、および(2) 20 人の異なる学生が取得した試験のスコア。
import pandas as pd #createDataFrame df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 8], ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82, 80, 88, 85, 90, 92, 94, 94, 88, 91, 96]}) #view first five rows of DataFrame df. head () hours score 0 1 75 1 1 66 2 1 68 3 2 74 4 2 78
1. 点群
次の構文を使用して、学習時間と試験結果の散布図を作成できます。
import matplotlib. pyplot as plt #create scatterplot of hours vs. score plt. scatter (df. hours , df. score ) plt. title (' Hours Studied vs. Exam Score ') plt. xlabel (' Hours Studied ') plt. ylabel (' Exam Score ')
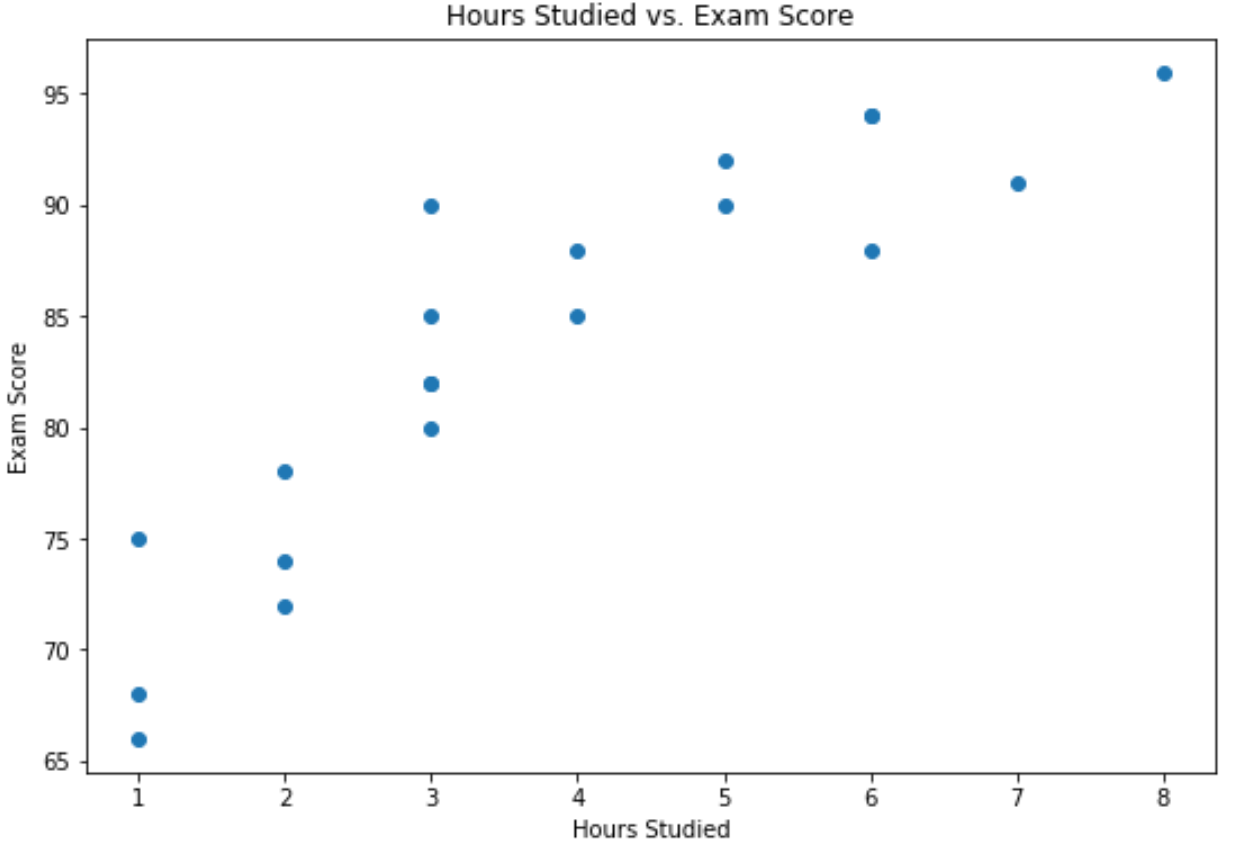
X 軸は学習時間を示し、Y 軸は試験で獲得した成績を示します。
グラフは、2 つの変数の間に正の関係があることを示しています。学習時間数が増加するにつれて、試験のスコアも増加する傾向があります。
2. 相関係数
ピアソン相関係数は、2 つの変数間の線形関係を定量化する方法です。
pandas のcorr()関数を使用して相関行列を作成できます。
#create correlation matrix df. corr () hours score hours 1.000000 0.891306 score 0.891306 1.000000
相関係数は0.891であることがわかります。これは、勉強時間と試験の成績の間に強い正の相関関係があることを示しています。
3. 単純な線形回帰
単純線形回帰は、2 つの変数間の関係を定量化するために使用できる統計手法です。
statsmodels パッケージのOLS()関数を使用すると、学習時間と受け取った試験結果に対する単純な線形回帰モデルをすばやく当てはめることができます。
import statsmodels. api as sm #define response variable y = df[' score '] #define explanatory variable x = df[[' hours ']] #add constant to predictor variables x = sm. add_constant (x) #fit linear regression model model = sm. OLS (y,x). fit () #view model summary print ( model.summary ()) OLS Regression Results ==================================================== ============================ Dept. Variable: R-squared score: 0.794 Model: OLS Adj. R-squared: 0.783 Method: Least Squares F-statistic: 69.56 Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07 Time: 16:15:52 Log-Likelihood: -55,886 No. Observations: 20 AIC: 115.8 Df Residuals: 18 BIC: 117.8 Model: 1 Covariance Type: non-robust ==================================================== ============================ coef std err t P>|t| [0.025 0.975] -------------------------------------------------- ---------------------------- const 69.0734 1.965 35.149 0.000 64.945 73.202 hours 3.8471 0.461 8.340 0.000 2.878 4.816 ==================================================== ============================ Omnibus: 0.171 Durbin-Watson: 1.404 Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177 Skew: 0.165 Prob(JB): 0.915 Kurtosis: 2.679 Cond. No. 9.37 ==================================================== ============================
近似された回帰式は次のようになります。
試験スコア = 69.0734 + 3.8471*(勉強時間)
これは、学習時間が追加されるごとに、試験スコアが平均3.8471増加することを示しています。
また、適合回帰式を使用して、合計学習時間数に基づいて生徒が受け取るスコアを予測することもできます。
たとえば、3 時間勉強した生徒は81.6147のスコアを取得する必要があります。
- 試験スコア = 69.0734 + 3.8471*(勉強時間)
- 試験のスコア = 69.0734 + 3.8471*(3)
- 試験結果 = 81.6147
追加リソース
次のチュートリアルでは、二変量解析に関する追加情報を提供します。