Python でエルボ法を使用して最適なクラスターを見つける方法
機械学習で最も一般的なクラスタリング アルゴリズムの 1 つは、k-means クラスタリングとして知られています。
K 平均法クラスタリングは、データセットの各観測値をK個のクラスターの 1 つに配置する手法です。
最終的な目標は、各クラスター内の観測値が互いによく似ている一方で、異なるクラスター内の観測値が互いにまったく異なるK個のクラスターを作成することです。
K 平均法クラスタリングを行う場合、最初のステップはKの値 (観測値を配置するクラスターの数) を選択することです。
Kの値を選択する最も一般的な方法の 1 つは、エルボ法として知られています。これには、x 軸にクラスターの数、y 軸に平方和の合計を使用してプロットを作成し、その後、プロット内で「膝」またはターンが現れる場所。
「ニー」が発生する x 軸上の点は、k-means クラスタリング アルゴリズムで使用する最適なクラスター数を示します。
次の例は、Python でエルボ メソッドを使用する方法を示しています。
ステップ 1: 必要なモジュールをインポートする
まず、K 平均法クラスタリングを実行するために必要なすべてのモジュールをインポートします。
import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler
ステップ 2: データフレームを作成する
次に、20 人の異なるバスケットボール選手の 3 つの変数を含む DataFrame を作成します。
#createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
np.nan, 9, 4, 3, 4, 12, 15, 11],
' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})
#drop rows with NA values in any columns
df = df. dropna ()
#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)
ステップ 3: エルボー法を使用して最適なクラスター数を見つける
K 平均法クラスタリングを使用して、これら 3 つのメトリクスに基づいて類似したアクターをグループ化したいとします。
Python で K-means クラスタリングを実行するには、 sklearnモジュールのKMeans関数を使用できます。
この関数の最も重要な引数はn_clustersで、観測値を配置するクラスターの数を指定します。
最適なクラスター数を決定するために、クラスター数とモデルの SSE (二乗誤差の合計) を表示するグラフを作成します。
次に、二乗和が「曲がる」か安定し始める「膝」を探します。この点は、クラスターの最適な数を表します。
次のコードは、x 軸にクラスターの数、y 軸に SSE を表示するこのタイプのプロットを作成する方法を示しています。
#initialize kmeans parameters kmeans_kwargs = { " init ": " random ", " n_init ": 10, " random_state ": 1, } #create list to hold SSE values for each k sse = [] for k in range(1, 11): kmeans = KMeans(n_clusters=k, ** kmeans_kwargs) kmeans. fit (scaled_df) sse. append (kmeans.inertia_) #visualize results plt. plot (range(1, 11), sse) plt. xticks (range(1, 11)) plt. xlabel (" Number of Clusters ") plt. ylabel (“ SSE ”) plt. show ()
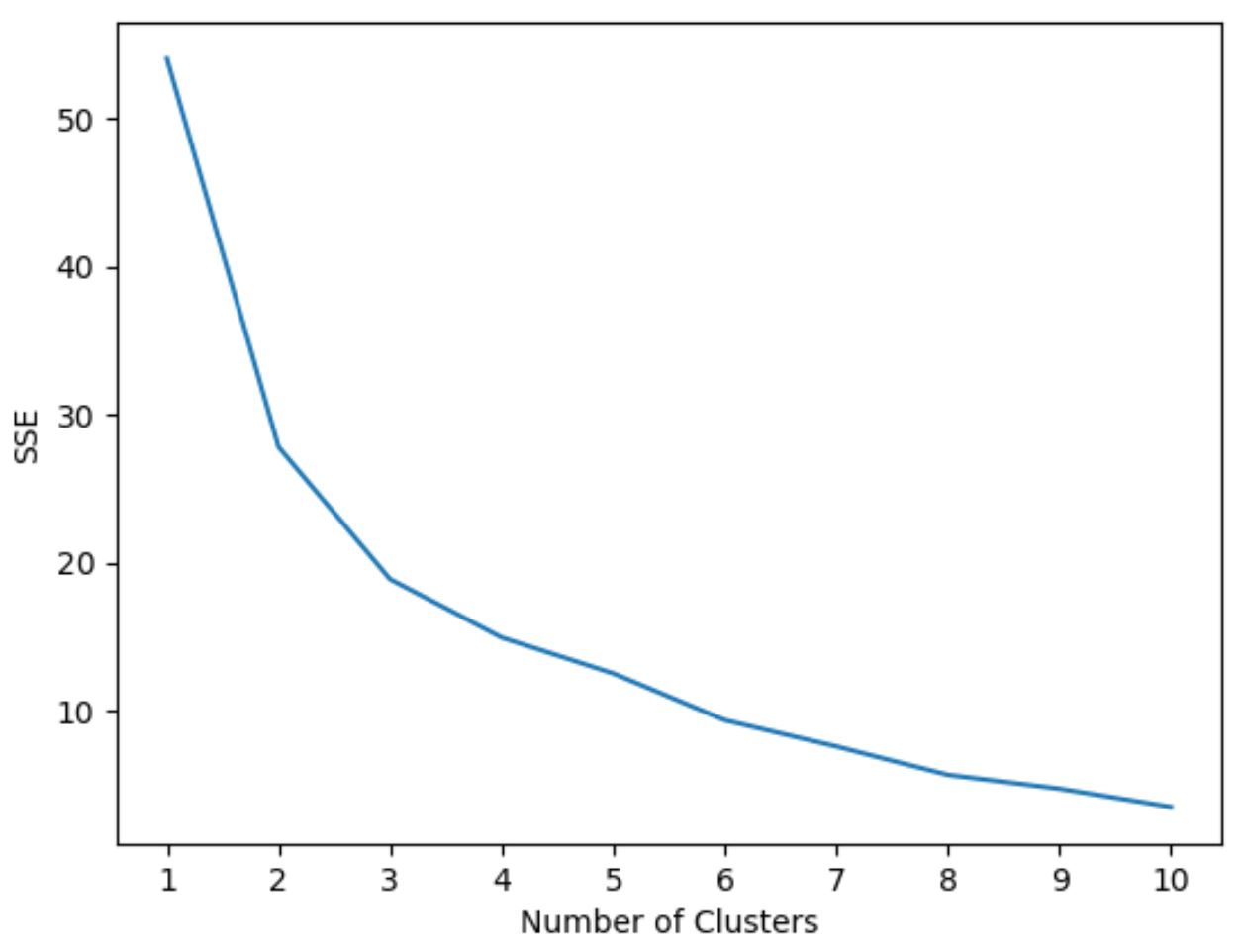
このグラフでは、 k = 3 クラスターにねじれまたは「ニー」があるように見えます。
したがって、次のステップで K-means クラスタリング モデルをフィッティングするときに 3 つのクラスターを使用します。
ステップ 4: 最適なKを使用して K-Means クラスタリングを実行する
次のコードは、 kの最適値 3 を使用してデータセットに対して k-means クラスタリングを実行する方法を示しています。
#instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )
#fit k-means algorithm to data
kmeans. fit (scaled_df)
#view cluster assignments for each observation
kmeans. labels_
array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0])
結果のテーブルには、DataFrame 内の各観測値のクラスター割り当てが表示されます。
これらの結果を解釈しやすくするために、各プレーヤーのクラスター割り当てを示す列を DataFrame に追加できます。
#append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_
#view updated DataFrame
print (df)
points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0
クラスター列には、各プレーヤーに割り当てられたクラスター番号 (0、1、または 2) が含まれます。
同じクラスターに属するプレーヤーは、ポイント、アシスト、リバウンドの列の値がほぼ似ています。
注: sklearnのKMeans関数の完全なドキュメントはここで見つけることができます。
追加リソース
次のチュートリアルでは、Python で他の一般的なタスクを実行する方法について説明します。
Python で線形回帰を実行する方法
Python でロジスティック回帰を実行する方法
Python で K-Fold 相互検証を実行する方法